Count palindromic characteristics of a String
Last Updated :
02 Mar, 2023
Given a string s of length n, count the number of substrings having different types of palindromic characteristics.
Palindromic Characteristic is the number of k-palindromes in a string where k lies in range [0, n).
A string is 1-palindrome(or simply palindrome) if and only if it reads the same backward as it reads forward.
A string is k-palindrome (k > 1) if and only if :
- Its left half is equal to its right half.
- Its left half and right half should be non-empty (k – 1)-palindrome. The left half of a string of length ‘t’ is its prefix of length ?t/2?, and the right half is the suffix of the same length.
Note: Each substring is counted as many times as it appears in the string. For example, in the string “aaa” the substring “a” appears 3 times.
Examples :
Input : abba
Output : 6 1 0 0
Explanation :
"6" 1-palindromes = "a", "b", "b", "a", "bb", "abba".
"1" 2-palindrome = "bb". Because "b" is 1-palindrome
and "bb" has both left and right parts equal.
"0" 3-palindrome and 4-palindrome.
Input : abacaba
Output : 12 4 1 0 0 0 0
Explanation :
"12" 1-palindromes = "a", "b", "a", "c", "a", "b",
"a", "aba", "aca", "aba", "bacab", "abacaba".
"4" 2-palindromes = "aba", "aca", "aba", "abacaba".
Because "a" and "aba" are 1-palindromes.
NOTE : "bacab" is not 2-palindrome as "ba"
is not 1-palindrome. "1" 3-palindrome = "abacaba".
Because is "aba" is 2-palindrome. "0" other
k-palindromes where 4 < = k < = 7.
Approach:
Take a string s and say it is a 1-palindrome and checking its left half also turns out to be a 1-palindrome then, obviously its right part will always be equal to the left part (as the string is also a 1-palindrome) making the original string to be 2-palindrome.
Now, similarly, checking the left half of the string, it also turns out to be a 1-palindrome then it will make the left half to be 2-palindrome and hence, making the original string to be 3-palindrome and so on checking it till only 1 alphabet is left or the part is not a 1-palindrome.
Let’s take string = “abacaba”. As known “abacaba” is 1-palindrome. So, when checking for its left half “aba”, which is also a 1-palindrome, it makes “abacaba” a 2-palindrome. Then, check for “aba”‘s left half “a” which is also a 1-palindrome. So it makes “aba” a 2-palindrome and “aba” makes “abacaba” a 3-palindrome. So in other words, if a string is a k-palindrome then it is also a (k-1)-palindrome, (k-2)-palindrome, and so on till 1-palindrome. Code for the same is given below which firsts check each and every substring if it is a palindrome or not and then counts the number of k-palindromic substrings recursively in logarithmic time.
Below is the implementation of above approach :
C++
#include <bits/stdc++.h>
using namespace std;
const int MAX_STR_LEN = 1000;
bool P[MAX_STR_LEN][MAX_STR_LEN];
int Kpal[MAX_STR_LEN];
void checkSubStrPal(string str, int n)
{
memset(P, false, sizeof(P));
for (int i = 0; i < n; i++)
P[i][i] = true;
for (int i = 0; i < n - 1; i++)
if (str[i] == str[i + 1])
P[i][i + 1] = true;
for (int gap = 2; gap < n; gap++)
{
for (int i = 0; i < n - gap; i++)
{
int j = gap + i;
if (str[i] == str[j] && P[i + 1][j - 1])
P[i][j] = true;
}
}
}
void countKPalindromes(int i, int j, int k)
{
if (i == j)
{
Kpal[k]++;
return;
}
if (P[i][j] == false)
return;
Kpal[k]++;
int mid = (i + j) / 2;
if ((j - i + 1) % 2 == 1)
mid--;
countKPalindromes(i, mid, k + 1);
}
void printKPalindromes(string s)
{
memset(Kpal, 0, sizeof(Kpal));
int n = s.length();
checkSubStrPal(s, n);
for (int i = 0; i < n; i++)
for (int j = 0; j < n - i; j++)
countKPalindromes(j, j + i, 1);
for (int i = 1; i <= n; i++)
cout << Kpal[i] << " ";
cout << "\n";
}
int main()
{
string s = "abacaba";
printKPalindromes(s);
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int MAX_STR_LEN = 1000;
static boolean P[][] =
new boolean[MAX_STR_LEN][MAX_STR_LEN];
static int []Kpal =
new int[MAX_STR_LEN];
static void checkSubStrPal(String str,
int n)
{
for (int i = 0; i < MAX_STR_LEN; i++)
{
for (int j = 0; j < MAX_STR_LEN; j++)
P[i][j] = false;
Kpal[i] = 0;
}
for (int i = 0; i < n; i++)
P[i][i] = true;
for (int i = 0; i < n - 1; i++)
if (str.charAt(i) == str.charAt(i + 1))
P[i][i + 1] = true;
for (int gap = 2; gap < n; gap++)
{
for (int i = 0; i < n - gap; i++)
{
int j = gap + i;
if (str.charAt(i) == str.charAt(j) &&
P[i + 1][j - 1])
P[i][j] = true;
}
}
}
static void countKPalindromes(int i, int j,
int k)
{
if (i == j)
{
Kpal[k]++;
return;
}
if (P[i][j] == false)
return;
Kpal[k]++;
int mid = (i + j) / 2;
if ((j - i + 1) % 2 == 1)
mid--;
countKPalindromes(i, mid, k + 1);
}
static void printKPalindromes(String s)
{
int n = s.length();
checkSubStrPal(s, n);
for (int i = 0; i < n; i++)
for (int j = 0; j < n - i; j++)
countKPalindromes(j, j + i, 1);
for (int i = 1; i <= n; i++)
System.out.print(Kpal[i] + " ");
System.out.println();
}
public static void main(String args[])
{
String s = "abacaba";
printKPalindromes(s);
}
}
|
Python3
MAX_STR_LEN = 1000;
P = [[0 for x in range(MAX_STR_LEN)]
for y in range(MAX_STR_LEN)] ;
for i in range(0, MAX_STR_LEN) :
for j in range(0, MAX_STR_LEN) :
P[i][j] = False;
Kpal = [0] * MAX_STR_LEN;
def checkSubStrPal(str, n) :
global P, Kpal, MAX_STR_LEN;
for i in range(0, MAX_STR_LEN) :
for j in range(0, MAX_STR_LEN) :
P[i][j] = False;
Kpal[i] = 0;
for i in range(0, n) :
P[i][i] = True;
for i in range(0, n - 1) :
if (str[i] == str[i + 1]) :
P[i][i + 1] = True;
for gap in range(2, n) :
for i in range(0, n - gap) :
j = gap + i;
if (str[i] == str[j] and
P[i + 1][j - 1]) :
P[i][j] = True;
def countKPalindromes(i, j, k) :
global Kpal, P;
if (i == j) :
Kpal[k] = Kpal[k] + 1;
return;
if (P[i][j] == False) :
return;
Kpal[k] = Kpal[k] + 1;
mid = int((i + j) / 2);
if ((j - i + 1) % 2 == 1) :
mid = mid - 1;
countKPalindromes(i, mid, k + 1);
def printKPalindromes(s) :
global P, Kpal, MAX_STR_LEN;
n = len(s);
checkSubStrPal(s, n);
for i in range(0, n) :
for j in range(0, n - i) :
countKPalindromes(j, j + i, 1);
for i in range(1, n + 1) :
print (Kpal[i], end=" ");
print();
s = "abacaba";
printKPalindromes(s);
|
C#
using System;
class GFG
{
static int MAX_STR_LEN = 1000;
static bool [,]P = new bool[MAX_STR_LEN,
MAX_STR_LEN];
static int []Kpal = new int[MAX_STR_LEN];
static void checkSubStrPal(string str,
int n)
{
for (int i = 0; i < MAX_STR_LEN; i++)
{
for (int j = 0; j < MAX_STR_LEN; j++)
P[i, j] = false;
Kpal[i] = 0;
}
for (int i = 0; i < n; i++)
P[i, i] = true;
for (int i = 0; i < n - 1; i++)
if (str[i] == str[i + 1])
P[i, i + 1] = true;
for (int gap = 2; gap < n; gap++)
{
for (int i = 0; i < n - gap; i++)
{
int j = gap + i;
if (str[i] == str[j] &&
P[i + 1, j - 1])
P[i, j] = true;
}
}
}
static void countKPalindromes(int i, int j,
int k)
{
if (i == j)
{
Kpal[k]++;
return;
}
if (P[i, j] == false)
return;
Kpal[k]++;
int mid = (i + j) / 2;
if ((j - i + 1) % 2 == 1)
mid--;
countKPalindromes(i, mid, k + 1);
}
static void printKPalindromes(string s)
{
int n = s.Length;
checkSubStrPal(s, n);
for (int i = 0; i < n; i++)
for (int j = 0; j < n - i; j++)
countKPalindromes(j, j + i, 1);
for (int i = 1; i <= n; i++)
Console.Write(Kpal[i] + " ");
Console.WriteLine();
}
static void Main()
{
string s = "abacaba";
printKPalindromes(s);
}
}
|
PHP
<?php
$MAX_STR_LEN = 1000;
$P = array(array());
$Kpal = array_fill(0, $MAX_STR_LEN, 0);
for($i = 0; $i < $MAX_STR_LEN; $i++)
{
for($j = 0; $j < $MAX_STR_LEN; $j++)
$P[$i][$j] = false;
}
function checkSubStrPal($str,
$n)
{
global $P, $Kpal,
$MAX_STR_LEN;
for ($i = 0;
$i < $MAX_STR_LEN; $i++)
{
for ($j = 0;
$j < $MAX_STR_LEN; $j++)
$P[$i][$j] = false;
$Kpal[$i] = 0;
}
for ($i = 0; $i < $n; $i++)
$P[$i][$i] = true;
for ($i = 0; $i < $n - 1; $i++)
if ($str[$i] == $str[$i + 1])
$P[$i][$i + 1] = true;
for ($gap = 2; $gap < $n; $gap++)
{
for ($i = 0;
$i < $n - $gap; $i++)
{
$j = $gap + $i;
if ($str[$i] == $str[$j] &&
$P[$i + 1][$j - 1])
$P[$i][$j] = true;
}
}
}
function countKPalindromes($i, $j, $k)
{
global $Kpal, $P;
if ($i == $j)
{
$Kpal[$k]++;
return;
}
if ($P[$i][$j] == false)
return;
$Kpal[$k]++;
$mid = ($i + $j) / 2;
if (($j - $i + 1) % 2 == 1)
$mid--;
countKPalindromes($i, $mid,
$k + 1);
}
function printKPalindromes($s)
{
global $P, $Kpal,
$MAX_STR_LEN;
$n = strlen($s);
checkSubStrPal($s, $n);
for ($i = 0; $i < $n; $i++)
for ($j = 0; $j < $n - $i; $j++)
countKPalindromes($j, $j +
$i, 1);
for ($i = 1; $i <= $n; $i++)
echo ($Kpal[$i] . " ");
echo("\n");
}
$s = "abacaba";
printKPalindromes($s);
?>
|
Javascript
let MAX_STR_LEN = 1000;
let P = new Array(MAX_STR_LEN);
for(let i = 0; i < MAX_STR_LEN; i++){
P[i] = new Array(MAX_STR_LEN);
}
let Kpal = new Array(MAX_STR_LEN);
function checkSubStrPal(str, n)
{
for(let i = 0; i < P.length; i++){
for(let j = 0; j < P[0].length; j++){
P[i][j] = false;
}
}
for (let i = 0; i < n; i++)
P[i][i] = true;
for (let i = 0; i < n - 1; i++)
if (str[i] == str[i + 1])
P[i][i + 1] = true;
for (let gap = 2; gap < n; gap++)
{
for (let i = 0; i < n - gap; i++)
{
let j = gap + i;
if (str[i] == str[j] && P[i + 1][j - 1])
P[i][j] = true;
}
}
}
function countKPalindromes(i, j, k)
{
if (i == j)
{
Kpal[k] = Kpal[k] + 1;
return;
}
if (P[i][j] == false)
return;
Kpal[k] = Kpal[k] + 1;
let mid = Math.floor((i + j) / 2);
if ((j - i + 1) % 2 == 1)
mid = mid - 1;
countKPalindromes(i, mid, k + 1);
}
function printKPalindromes(s)
{
for(let i = 0; i < Kpal.length; i++){
Kpal[i] = 0;
}
let n = s.length;
checkSubStrPal(s, n);
for (let i = 0; i < n; i++)
for (let j = 0; j < n - i; j++)
countKPalindromes(j, j + i, 1);
for (let i = 1; i <= n; i++)
console.log(Kpal[i] + " ");
}
let s = "abacaba";
printKPalindromes(s);
|
Complexity Analysis:
- Time Complexity : O(
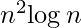 )
) - Auxiliary Space : O(
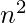 )
)
Share your thoughts in the comments
Please Login to comment...