Count number of trailing zeros in (1^1)*(2^2)*(3^3)*(4^4)*..
Last Updated :
23 Jun, 2022
Given an integer n, the task is to find the number of trailing zeros in the function 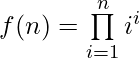 i.e. f(n) = 11 * 22 * 33 * … * nn.
i.e. f(n) = 11 * 22 * 33 * … * nn.
Examples:
Input: n = 5
Output: 5
f(5) = 11 * 22 * 33 * 44 * 55 = 1 * 4 * 27 * 256 * 3125 = 86400000
Input: n = 12
Output: 15
Approach: We know that 5 * 2 = 10 i.e. 1 trailing zero is the result of the multiplication of a single 5 and a single 2. So, if we have x number of 5 and y number of 2 then the number of trailing zeros will be min(x, y).
Now, for every number i in the series, we need to count the number of 2 and 5 in its factors say x and y but the number of 2s and 5s will be x * i and y * i respectively because in the series i is raised to the power itself i.e. ii. Count the number of 2s and 5s in the complete series and print the minimum of them which is the required answer.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int trailing_zeros(int N)
{
int count_of_two = 0, count_of_five = 0;
for (int i = 1; i <= N; i++) {
int val = i;
while (val % 2 == 0 && val > 0) {
val /= 2;
count_of_two += i;
}
while (val % 5 == 0 && val > 0) {
val /= 5;
count_of_five += i;
}
}
int ans = min(count_of_two, count_of_five);
return ans;
}
int main()
{
int N = 12;
cout << trailing_zeros(N);
return 0;
}
|
Java
class GFG
{
static int trailing_zeros(int N)
{
int count_of_two = 0, count_of_five = 0;
for (int i = 1; i <= N; i++)
{
int val = i;
while (val % 2 == 0 && val > 0)
{
val /= 2;
count_of_two += i;
}
while (val % 5 == 0 && val > 0)
{
val /= 5;
count_of_five += i;
}
}
int ans = Math.min(count_of_two, count_of_five);
return ans;
}
public static void main (String[] args)
{
int N = 12;
System.out.println(trailing_zeros(N));
}
}
|
Python3
def trailing_zeros(N):
count_of_two = 0
count_of_five = 0
for i in range(1, N + 1, 1):
val = i
while (val % 2 == 0 and val > 0):
val /= 2
count_of_two += i
while (val % 5 == 0 and val > 0):
val /= 5
count_of_five += i
ans = min(count_of_two, count_of_five)
return ans
if __name__ == '__main__':
N = 12
print(trailing_zeros(N))
|
C#
using System;
class GFG
{
static int trailing_zeros(int N)
{
int count_of_two = 0, count_of_five = 0;
for (int i = 1; i <= N; i++)
{
int val = i;
while (val % 2 == 0 && val > 0)
{
val /= 2;
count_of_two += i;
}
while (val % 5 == 0 && val > 0)
{
val /= 5;
count_of_five += i;
}
}
int ans = Math.Min(count_of_two, count_of_five);
return ans;
}
public static void Main()
{
int N = 12;
Console.WriteLine(trailing_zeros(N));
}
}
|
PHP
<?php
function trailing_zeros($N)
{
$count_of_two = 0;
$count_of_five = 0;
for ($i = 1; $i <= $N; $i++)
{
$val = $i;
while ($val % 2 == 0 && $val > 0)
{
$val /= 2;
$count_of_two += $i;
}
while ($val % 5 == 0 && $val > 0)
{
$val /= 5;
$count_of_five += $i;
}
}
$ans = min($count_of_two, $count_of_five);
return $ans;
}
$N = 12;
echo trailing_zeros($N);
?>
|
Javascript
<script>
function trailing_zeros(N)
{
let count_of_two = 0, count_of_five = 0;
for(let i = 1; i <= N; i++)
{
let val = i;
while (val % 2 == 0 && val > 0)
{
val = parseInt(val / 2);
count_of_two += i;
}
while (val % 5 == 0 && val > 0)
{
val = parseInt(val / 5);
count_of_five += i;
}
}
let ans = Math.min(count_of_two,
count_of_five);
return ans;
}
let N = 12;
document.write(trailing_zeros(N));
</script>
|
Time Complexity: O(N * (log2N + log5N))
Auxiliary Space: O(1), since no extra space has been taken.
Share your thoughts in the comments
Please Login to comment...