Container with Most Water

Given n non-negative integers 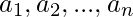where each represents a point at coordinate 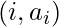. ‘ n ‘ vertical lines are drawn such that the two endpoints of line i is at 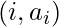and .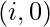 
Find two lines, which together with x-axis forms a container, such that the container contains the most water.
The program should return an integer which corresponds to the maximum area of water that can be contained (maximum area instead of maximum volume sounds weird but this is the 2D plane we are working with for simplicity).

Note: You may not slant the container. 

Examples :

Input: array = [1, 5, 4, 3]
Output: 6
Explanation : 
5 and 3 are distance 2 apart. 
So the size of the base = 2. 
Height of container = min(5, 3) = 3. 
So total area = 3 * 2 = 6

Input: array = [3, 1, 2, 4, 5]
Output: 12
Explanation : 
5 and 3 are distance 4 apart. 
So the size of the base = 4. 
Height of container = min(5, 3) = 3. 
So total area = 4 * 3 = 12

Naive Solution:

• Approach: The idea is quite simple and involves checking every pair of boundaries or array element and find out the maximum area under any pair of boundaries.
• Algorithm:
  1. Create a nested loop, the outer loop traverses the array from 0 to end (index of this loop is i).
  2. The inner loop traverses the array from i + 1 to end (index of this loop is j).
  3. Find the water that can be contained in the container with height of boundaries as array[i] and array[j], i.e area = (j – i)* min(array[i],array[j]), if this area is greater than current maximum, update the current maximum
  4. Print the current maximum.
• Implementation:

C++14

// C++ code for Max
// Water Container
#include <iostream>
using namespace std;

int maxArea(int A[], int len)
{
    int area = 0;
    for (int i = 0; i < len; i++) {
        for (int j = i + 1; j < len; j++) {
            // Calculating the max area
            area = max(area, min(A[j], A[i]) * (j - i));
        }
    }
    return area;
}

// Driver code
int main()
{
    int a[] = { 1, 5, 4, 3 };
    int b[] = { 3, 1, 2, 4, 5 };

    int len1 = sizeof(a) / sizeof(a[0]);
    cout << maxArea(a, len1);

    int len2 = sizeof(b) / sizeof(b[0]);
    cout << endl << maxArea(b, len2);
}

Java

// Java code for Max
// Water Container
import java.io.*;

class GFG{

public static int maxArea(int[] a)
{

    int Area = 0;

    for(int i = 0; i < a.length; i++)
    {
        for(int j = i + 1; j < a.length; j++)
        {
            Area = Math.max(
                Area, Math.min(a[i], a[j]) *
                              (j - i));
        }
    }
    return Area;
}

// Driver code
public static void main(String[] args)
{
    int a[] = { 1, 5, 4, 3 };
    int b[] = { 3, 1, 2, 4, 5 };

    System.out.println(maxArea(a));
    System.out.println(maxArea(b));
}
}

// This code is contributed by mulchandanimanisha5

Python3

# Python3 code for Max
# Water Container
def maxArea(A, Len) :
    area = 0
    for i in range(Len) :
        for j in range(i + 1, Len) :

            # Calculating the max area
            area = max(area, min(A[j], A[i]) * (j - i))
    return area

# Driver code
a = [ 1, 5, 4, 3 ]
b = [ 3, 1, 2, 4, 5 ]

len1 = len(a)
print(maxArea(a, len1))

len2 = len(b)
print(maxArea(b, len2))

# This code is contributed by divyesh072019.

C#

// C# code for Max
// Water Container
using System;
class GFG
{

public static int maxArea(int[] a)
{

    int Area = 0;

    for(int i = 0; i < a.Length; i++)
    {
        for(int j = i + 1; j < a.Length; j++)
        {
            Area = Math.Max(Area, Math.Min(a[i], a[j]) *
                            (j - i));
        }
    }
    return Area;
}

// Driver code
public static void Main(String[] args)
{
    int []a = { 1, 5, 4, 3 };
    int []b = { 3, 1, 2, 4, 5 };

    Console.WriteLine(maxArea(a));
    Console.Write(maxArea(b));
}
}

// This code is contributed by shivanisinghss2110

Javascript

<script>
    // Javascript code for Max
    // Water Container

    function maxArea(A, len)
    {
        let area = 0;
        for (let i = 0; i < len; i++) {
            for (let j = i + 1; j < len; j++) {
                // Calculating the max area
                area = Math.max(area, Math.min(A[j], A[i]) * (j - i));
            }
        }
        return area;
    }

      let a = [ 1, 5, 4, 3 ];
    let b = [ 3, 1, 2, 4, 5 ];

    let len1 = a.length;
    document.write(maxArea(a, len1) + "</br>");

    let len2 = b.length;
    document.write(maxArea(b, len2));

    // This code is contributed by mukesh07.
</script>

Output:

6
12

Complexity Analysis:

• Time Complexity: O(n^2). 
  As nested traversal of the array is required, so time complexity is O(n^2)
• Space Complexity: O(1). 
  As no extra space is required, so space complexity is constant.

Efficient Solution:

• Approach: Given an array of heights of lines of boundaries of the container, find the maximum water that can be stored in a container. So start with the first and last element and check the amount of water that can be contained and store that container. Now the question arises is there any better boundaries or lines that can contain maximum water. So there is a clever way to find that. Initially, there are two indices the first and last index pointing to the first and the last element (which acts as boundaries of the container), if the value of first index is less than the value of last index increase the first index else decrease the last index. As the decrease in width is constant, by following the above process the optimal answer can be reached.
  The GIF below explains the approach

• Algorithm:
  1. Keep two index, first = 0 and last = n-1 and a value max_area that stores the maximum area.
  2. Run a loop until first is less than the last.
  3. Update the max_area with maximum of max_area and min(array[first] , array[last])*(last-first)
  4. if the value at array[first] is greater the array[last] then update last as last – 1 else update first as first + 1
  5. Print the maximum area.
• Implementation:

C++

// C++ code for Max
// Water Container
#include<iostream>
using namespace std;

int maxArea(int A[], int len)
{
    int l = 0;
    int r = len -1;
    int area = 0;

    while (l < r)
    {
        // Calculating the max area
        area = max(area, min(A[l],
                        A[r]) * (r - l));

            if (A[l] < A[r])
                l += 1;

            else
                r -= 1;
    }
    return area;
}

// Driver code
int main()
{
    int a[] = {1, 5, 4, 3};
    int b[] = {3, 1, 2, 4, 5};

    int len1 = sizeof(a) / sizeof(a[0]);
    cout << maxArea(a, len1);

    int len2 = sizeof(b) / sizeof(b[0]);
    cout << endl << maxArea(b, len2);
}

// This code is contributed by Smitha Dinesh Semwal

Java

// Java code for Max
// Water Container
import java.util.*;

class Area{

    public static int maxArea(int A[], int len)
    {
        int l = 0;
        int r = len -1;
        int area = 0;

        while (l < r)
        {
            // Calculating the max area
            area = Math.max(area,
                        Math.min(A[l], A[r]) * (r - l));

            if (A[l] < A[r])
                l += 1;

            else
                r -= 1;
        }
        return area;
    }

    public static void main(String[] args)
    {
        int a[] = {1, 5, 4, 3};
        int b[] = {3, 1, 2, 4, 5};

        int len1 = 4;
        System.out.print( maxArea(a, len1)+"\n" );

        int len2 = 5;
        System.out.print( maxArea(b, len2) );
    }
}

// This code is contributed by rishabh_jain

Python3

# Python3 code for Max
# Water Container
def maxArea( A):
    l = 0
    r = len(A) -1
    area = 0

    while l < r:
        # Calculating the max area
        area = max(area, min(A[l],
                        A[r]) * (r - l))

        if A[l] < A[r]:
            l += 1
        else:
            r -= 1
    return area

# Driver code
a = [1, 5, 4, 3]
b = [3, 1, 2, 4, 5]

print(maxArea(a))
print(maxArea(b))

C#

// C# code for Max
// Water Container
using System;

class Area{

    public static int maxArea(int []A, int len)
    {
        int l = 0;
        int r = len -1;
        int area = 0;

        while (l < r)
        {
            // Calculating the max area
            area = Math.Max(area,
                        Math.Min(A[l], A[r]) * (r - l));

            if (A[l] < A[r])
                l += 1;

            else
                r -= 1;
        }
        return area;
    }

    // Driver code
    public static void Main()
    {
        int []a = {1, 5, 4, 3};
        int []b = {3, 1, 2, 4, 5};

        int len1 = 4;
        Console.WriteLine( maxArea(a, len1));

        int len2 = 5;
        Console.WriteLine( maxArea(b, len2) );
    }
}

// This code is contributed by Vt_M

PHP

<?php
// PHP code for Max
// Water Container
function maxArea($A, $len)
{
    $l = 0;
    $r = $len -1;
    $area = 0;

    while ($l < $r)
    {
        // Calculating the max area
        $area = max($area, min($A[$l],
                    $A[$r]) * ($r - $l));

            if ($A[$l] < $A[$r])
                $l += 1;

            else
                $r -= 1;
    }
    return $area;
}

// Driver code
$a = array(1, 5, 4, 3);
$b = array(3, 1, 2, 4, 5);

$len1 = sizeof($a) / sizeof($a[0]);
echo maxArea($a, $len1). "\n";

$len2 = sizeof($b) / sizeof($b[0]);
echo maxArea($b, $len2);

// This code is contributed by mits
?>

Javascript

<script>

// Javascript code for Max
// Water Container
function maxArea(A, len)
{
    let l = 0;
    let r = len -1;
    let area = 0;

    while (l < r)
    {

        // Calculating the max area
        area = Math.max(area, Math.min(A[l],
                        A[r]) * (r - l));

        if (A[l] < A[r])
            l += 1;
        else
            r -= 1;
    }
    return area;
}

// Driver code
let a = [ 1, 5, 4, 3 ];
let b = [ 3, 1, 2, 4, 5 ];

let len1 = a.length;
document.write(maxArea(a, len1) + "</br>");

let len2 = b.length;
document.write(maxArea(b, len2));

// This code is contributed by rameshtravel07

</script>

Output

6
12

Complexity Analysis:

• Time Complexity: O(n). 
  As only one traversal of the array is required, so time complexity is O(n).
• Space Complexity: O(1). 
  No extra space is required, so space complexity is constant.

Solution Analysis – Why this solution works?

Everytime, we are moving our pointer i ahead if height of line at ith index is smaller or j pointer if height of line at jth index is smaller. This means whichever line is smaller, we won’t consider it again, because, this line could be the answer only if the other line is larger than it and at maximum width and to be noticed that this is the time when other line is larger as well as max distance apart. So, not considering it makes sense.

In other words, we are required to pair up every line with that line which is greater than it and at maximum distance apart i.e. 

For example -> 8 5 9 1 10 2 6

here, if 8 has to be in the answer then other line that we choose should be 10 as it is the first line from the end that is at maximum distance apart from 8 and longer than 8. Hence, for 8 to be in the answer, other line should be 10.

Now, Lets assume i at 8 and j at 10. Compare it and move the pointer i to 5.

Now, you may ask, ok, you have moved the pointer i to 5 but can it not happen that 5 could pair up with other lines after 10 as we have neglected those lines by moving j pointer to 10.

So, to be noticed that if 5 would have been in the answer then any line after 10 must be >= 5 and if there is any line after 10 whose height is greater than or equal to 5 then its contribution would surely have been calculated while pointer ‘i’ was at 8.

So, for the combinations of lines which we are neglecting, have been already taken care of.