Count elements in an Array that can be represented as difference of two perfect squares
Last Updated :
20 Sep, 2022
Given an array arr[], the task is to count the number of elements in the array that can be represented as in the form of the difference of two perfect square numbers. 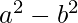
Examples:
Input: arr[] = {1, 2, 3}
Output: 2
Explanation:
There are two such elements that can be represented as
difference of square of two numbers –
Element 1 – 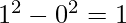
Element 3 – 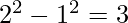
Therefore, Count of such elements is 2.
Input: arr[] = {2, 5, 6}
Output: 1
Explanation:
There is only one such element. That is –
Element 5 – 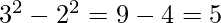
Therefore, Count of such elements is 1.
Approach: The key observation in the problem is numbers which can be represented as the difference of the squares of two numbers never yield 2 as the remainder when divided by 4.
For Example:
N = 4 => 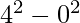
N = 6 => Can’t be represented as 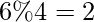
N = 8 => 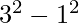
N = 10 => Can’t be represented as 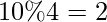
Therefore, iterate over the array and count the number of such elements in the array.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int count_num(int arr[], int n)
{
int count = 0;
for (int i = 0; i < n; i++)
if ((arr[i] % 4) != 2)
count++;
cout << count;
return 0;
}
int main()
{
int arr[] = { 1, 2, 3 };
int n = sizeof(arr) / sizeof(arr[0]);
count_num(arr, n);
return 0;
}
|
Java
class GFG{
static void count_num(int []arr, int n)
{
int count = 0;
for(int i = 0; i < n; i++)
{
if ((arr[i] % 4) != 2)
count++;
}
System.out.println(count);
}
public static void main (String[] args)
{
int arr[] = { 1, 2, 3 };
int n = arr.length;
count_num(arr, n);
}
}
|
Python3
def count_num(arr, n):
count = 0
for i in arr:
if ((i % 4) != 2):
count = count + 1
return count
if __name__ == "__main__":
arr = [1, 2, 3]
n = len(arr)
print(count_num(arr, n))
|
C#
using System;
class GFG{
static void count_num(int []arr, int n)
{
int count = 0;
for(int i = 0; i < n; i++)
{
if ((arr[i] % 4) != 2)
count++;
}
Console.WriteLine(count);
}
public static void Main(string[] args)
{
int []arr = { 1, 2, 3 };
int n = arr.Length;
count_num(arr, n);
}
}
|
Javascript
<script>
function count_num(arr, n)
{
let count = 0;
for (let i = 0; i < n; i++)
if ((arr[i] % 4) != 2)
count++;
document.write(count);
return 0;
}
let arr = [ 1, 2, 3 ];
let n = arr.length;
count_num(arr, n);
</script>
|
Time complexity: O(n) where n is the number of elements in the given array
Auxiliary space: O(1)
Share your thoughts in the comments
Please Login to comment...