Closest perfect square and its distance

Given a positive integer 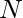. The task is to find the perfect square number closest to N and steps required to reach this number from N.
Note: The closest perfect square to N can be either less than, equal to or greater than N and steps are referred to as the difference between N and the closest perfect square.
Examples:

Input: N = 1500 
Output: Perfect square = 1521, Steps = 21 
For N = 1500 
Closest perfect square greater than N is 1521. 
So steps required is 21. 
Closest perfect square less than N is 1444. 
So steps required is 56. 
The minimum of these two is 1521 with steps 21.
Input: N = 2 
Output: Perfect Square = 1, Steps = 1 
For N = 2 
Closest perfect square greater than N is 4. 
So steps required is 2. 
Closest perfect square less than N is 1. 
So steps required is 1. 
The minimum of these two is 1. 

Approach 1:

• If N is a perfect square then print N and steps as 0.
• Else, find the first perfect square number > N and note its difference with N.
• Then, find the first perfect square number < N and note its difference with N.
• And print the perfect square resulting in the minimum of these two differences obtained and also the difference as the minimum steps.

Below is the implementation of the above approach: 

C++

// CPP program to find the closest perfect square
// taking minimum steps to reach from a number

#include <bits/stdc++.h>
using namespace std;

// Function to check if a number is
// perfect square or not
bool isPerfect(int N)
{
    if ((sqrt(N) - floor(sqrt(N))) != 0)
        return false;
    return true;
}

// Function to find the closest perfect square
// taking minimum steps to reach from a number
void getClosestPerfectSquare(int N)
{
    if (isPerfect(N)) {
        cout << N << " "
             << "0" << endl;
        return;
    }

    // Variables to store first perfect
    // square number
    // above and below N
    int aboveN = -1, belowN = -1;
    int n1;

    // Finding first perfect square
    // number greater than N
    n1 = N + 1;
    while (true) {
        if (isPerfect(n1)) {
            aboveN = n1;
            break;
        }
        else
            n1++;
    }

    // Finding first perfect square
    // number less than N
    n1 = N - 1;
    while (true) {
        if (isPerfect(n1)) {
            belowN = n1;
            break;
        }
        else
            n1--;
    }

    // Variables to store the differences
    int diff1 = aboveN - N;
    int diff2 = N - belowN;

    if (diff1 > diff2)
        cout << belowN << " " << diff2;
    else
        cout << aboveN << " " << diff1;
}

// Driver code
int main()
{
    int N = 1500;

    getClosestPerfectSquare(N);
}
// This code is contributed by
// Surendra_Gangwar

Java

// Java program to find the closest perfect square
// taking minimum steps to reach from a number

class GFG {

    // Function to check if a number is
    // perfect square or not
    static boolean isPerfect(int N)
    {
        if ((Math.sqrt(N) - Math.floor(Math.sqrt(N))) != 0)
            return false;
        return true;
    }

    // Function to find the closest perfect square
    // taking minimum steps to reach from a number
    static void getClosestPerfectSquare(int N)
    {
        if (isPerfect(N)) {
            System.out.println(N + " "
                               + "0");
            return;
        }

        // Variables to store first perfect
        // square number
        // above and below N
        int aboveN = -1, belowN = -1;
        int n1;

        // Finding first perfect square
        // number greater than N
        n1 = N + 1;
        while (true) {
            if (isPerfect(n1)) {
                aboveN = n1;
                break;
            }
            else
                n1++;
        }

        // Finding first perfect square
        // number less than N
        n1 = N - 1;
        while (true) {
            if (isPerfect(n1)) {
                belowN = n1;
                break;
            }
            else
                n1--;
        }

        // Variables to store the differences
        int diff1 = aboveN - N;
        int diff2 = N - belowN;

        if (diff1 > diff2)
            System.out.println(belowN + " " + diff2);
        else
            System.out.println(aboveN + " " + diff1);
    }

    // Driver code
    public static void main(String args[])
    {
        int N = 1500;

        getClosestPerfectSquare(N);
    }
}

Python3

# Python3 program to find the closest
# perfect square taking minimum steps
# to reach from a number

# Function to check if a number is
# perfect square or not
from math import sqrt, floor


def isPerfect(N):
    if (sqrt(N) - floor(sqrt(N)) != 0):
        return False
    return True

# Function to find the closest perfect square
# taking minimum steps to reach from a number


def getClosestPerfectSquare(N):
    if (isPerfect(N)):
        print(N, "0")
        return

    # Variables to store first perfect
    # square number above and below N
    aboveN = -1
    belowN = -1
    n1 = 0

    # Finding first perfect square
    # number greater than N
    n1 = N + 1
    while (True):
        if (isPerfect(n1)):
            aboveN = n1
            break
        else:
            n1 += 1

    # Finding first perfect square
    # number less than N
    n1 = N - 1
    while (True):
        if (isPerfect(n1)):
            belowN = n1
            break
        else:
            n1 -= 1

    # Variables to store the differences
    diff1 = aboveN - N
    diff2 = N - belowN

    if (diff1 > diff2):
        print(belowN, diff2)
    else:
        print(aboveN, diff1)


# Driver code
N = 1500
getClosestPerfectSquare(N)

# This code is contributed
# by sahishelangia

C#

// C# program to find the closest perfect square
// taking minimum steps to reach from a number
using System;

class GFG {

    // Function to check if a number is
    // perfect square or not
    static bool isPerfect(int N)
    {
        if ((Math.Sqrt(N) - Math.Floor(Math.Sqrt(N))) != 0)
            return false;
        return true;
    }

    // Function to find the closest perfect square
    // taking minimum steps to reach from a number
    static void getClosestPerfectSquare(int N)
    {
        if (isPerfect(N)) {
            Console.WriteLine(N + " "
                              + "0");
            return;
        }

        // Variables to store first perfect
        // square number
        // above and below N
        int aboveN = -1, belowN = -1;
        int n1;

        // Finding first perfect square
        // number greater than N
        n1 = N + 1;
        while (true) {
            if (isPerfect(n1)) {
                aboveN = n1;
                break;
            }
            else
                n1++;
        }

        // Finding first perfect square
        // number less than N
        n1 = N - 1;
        while (true) {
            if (isPerfect(n1)) {
                belowN = n1;
                break;
            }
            else
                n1--;
        }

        // Variables to store the differences
        int diff1 = aboveN - N;
        int diff2 = N - belowN;

        if (diff1 > diff2)
            Console.WriteLine(belowN + " " + diff2);
        else
            Console.WriteLine(aboveN + " " + diff1);
    }

    // Driver code
    public static void Main()
    {
        int N = 1500;

        getClosestPerfectSquare(N);
    }
}
// This code is contributed by anuj_67..

PHP

<?php
// PHP program to find the closest perfect
// square taking minimum steps to reach
// from a number

// Function to check if a number is
// perfect square or not
function isPerfect($N)
{
    if ((sqrt($N) - floor(sqrt($N))) != 0)
        return false;
    return true;
}

// Function to find the closest perfect square
// taking minimum steps to reach from a number
function getClosestPerfectSquare($N)
{
    if (isPerfect($N))
    {
        echo $N, " ", "0", "\n";
        return;
    }

    // Variables to store first perfect
    // square number
    // above and below N
    $aboveN = -1;
    $belowN = -1;
    $n1;

    // Finding first perfect square
    // number greater than N
    $n1 = $N + 1;
    while (true)
    {
        if (isPerfect($n1))
        {
            $aboveN = $n1;
            break;
        }
        else
            $n1++;
    }

    // Finding first perfect square
    // number less than N
    $n1 = $N - 1;
    while (true)
    {
        if (isPerfect($n1))
        {
            $belowN = $n1;
            break;
        }
        else
            $n1--;
    }

    // Variables to store the differences
    $diff1 = $aboveN - $N;
    $diff2 = $N - $belowN;

    if ($diff1 > $diff2)
        echo $belowN, " " , $diff2;
    else
        echo $aboveN, " ", $diff1;
}

// Driver code
$N = 1500;
getClosestPerfectSquare($N);

// This code is contributed by ajit.
?>

Javascript

<script>

    // Javascript program to find
    // the closest perfect square
    // taking minimum steps to reach
    // from a number

    // Function to check if a number is
    // perfect square or not
    function isPerfect(N)
    {
        if ((Math.sqrt(N) -
        Math.floor(Math.sqrt(N))) != 0)
            return false;
        return true;
    }

    // Function to find the closest perfect square
    // taking minimum steps to reach from a number
    function getClosestPerfectSquare(N)
    {
        if (isPerfect(N)) {
            document.write(N + " " + "0" + "</br>");
            return;
        }

        // Variables to store first perfect
        // square number
        // above and below N
        let aboveN = -1, belowN = -1;
        let n1;

        // Finding first perfect square
        // number greater than N
        n1 = N + 1;
        while (true) {
            if (isPerfect(n1)) {
                aboveN = n1;
                break;
            }
            else
                n1++;
        }

        // Finding first perfect square
        // number less than N
        n1 = N - 1;
        while (true) {
            if (isPerfect(n1)) {
                belowN = n1;
                break;
            }
            else
                n1--;
        }

        // Variables to store the differences
        let diff1 = aboveN - N;
        let diff2 = N - belowN;

        if (diff1 > diff2)
            document.write(belowN + " " + diff2);
        else
            document.write(aboveN + " " + diff1);
    }

    let N = 1500;

      getClosestPerfectSquare(N);

</script>

Output

1521 21

Time Complexity: O(n), where n is the given number since we are using brute force to find the above and below perfect squares.

Space Complexity: O(1), since no extra space has been taken.

Approach 2:

The above method might take a lot of time for bigger numbers i.e. greater than 10⁶. We would wish to have a faster way to do that.

• Here, we will use maths to solve the above problem in constant time complexity.
• We will first find the square root of the number n. 
• We will check if n was a perfect square, and if it was, we will return 0 there itself.
• Else, we will use its square root to find the just above and below perfect square numbers, and return the one which is at the minimum distance.

Below is the implementation of the above approach: 

C++

// CPP program to find the closest perfect square
// taking minimum steps to reach from a number

#include <bits/stdc++.h>
using namespace std;


// Function to find the closest perfect square
// taking minimum steps to reach from a number
void getClosestPerfectSquare(int N)
{
  int x = sqrt(N);

  //Checking if N is a perfect square
  if((x*x)==N){
    cout<<N<<" "<<0;
    return;
  }

  // If N is not a perfect square,
  // squaring x and x+1 gives us the
  // just below and above perfect squares

    // Variables to store perfect
    // square number just
    // above and below N
    int aboveN = (x+1)*(x+1), belowN = x*x;

    // Variables to store the differences
    int diff1 = aboveN - N;
    int diff2 = N - belowN;

    if (diff1 > diff2)
        cout << belowN << " " << diff2;
    else
        cout << aboveN << " " << diff1;
}

// Driver code
int main()
{
    int N = 1500;

    getClosestPerfectSquare(N);
}
// This code is contributed by
// Rohit Kumar

Python3

# Python3 program to find the closest
# perfect square taking minimum steps
# to reach from a number

from math import sqrt, floor

# Function to find the closest perfect square
# taking minimum steps to reach from a number


def getClosestPerfectSquare(N):
    x = floor(sqrt(N))

    # Checking if N is itself a perfect square
    if (sqrt(N) - floor(sqrt(N)) == 0):
        print(N,0)
        return

    # Variables to store first perfect
    # square number above and below N
    aboveN = (x+1)*(x+1)
    belowN = x*x

    # Variables to store the differences
    diff1 = aboveN - N
    diff2 = N - belowN

    if (diff1 > diff2):
        print(belowN, diff2)
    else:
        print(aboveN, diff1)


# Driver code
N = 1500
getClosestPerfectSquare(N)

# This code is contributed
# by Rohit Kumar

Output

1521 21

Time Complexity: O(1), since we have used only maths here.

Space Complexity: O(1), since no extra space has been taken.