Coplanarity of Two Lines in 3D Geometry
Last Updated :
10 May, 2021
Given two lines L1 and L2, each passing through a point whose position vector are given as (X, Y, Z) and parallel to line whose direction ratios are given as (a, b, c), the task is to check whether line L1 and L2 are coplanar or not.
Coplanar: If two lines are in a same plane then lines can be called as coplanar.
Example:
Input:
L1: (x1, y1, z1) = (-3, 1, 5) and (a1, b1, c1) = (-3, 1, 5)
L2: (x1, y1, z1) = (-1, 2, 5) and (a1, b1, c1) = (-1, 2, 5)
Output: Lines are Coplanar
Input:
L1: (x1, y1, z1) = (1, 2, 3) and (a1, b1, c1) = (2, 4, 6)
L2: (x1, y1, z1) = (-1, -2, -3) and (a1, b1, c1) = (3, 4, 5)
Output: Lines are Non-Coplanar
Approach:
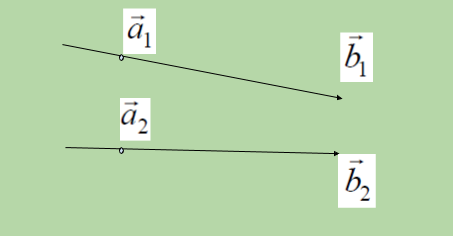
There are two ways to express a line in 3 dimensions:
Vector Form:
The equation of two lines whose coplanarity is to be determined in vector form.
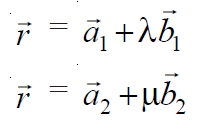
In the above equation of a line, a vector is a point in the 3D plane from which a given line is passing through called as position vector a and b vector is the vector line in the 3D plane to which our given line is parallel. So it can be said that the line(1) passes through the point, say A, with position vector a1 and is parallel to vector b1 and the line(2) passes through the point, say B with position vector a2 and is parallel to vector b2. Therefore:
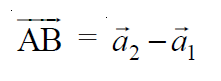
The given lines are coplanar if and only if AB vector is perpendicular to the cross product of vectors b1 and b2 i.e.,
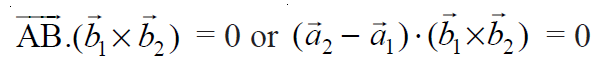
Here the cross product of vectors b1 and b2 will give another vector line that will be perpendicular to both b1 and b2 vector lines. and AB is the line vector joining the position vectors a1 and a2 of two given lines. Now, check whether two lines are coplanar or not by determining above dot product is zero or not.
Cartesian Form:
Let (x1, y1, z1) and (x2, y2, z2) be the coordinates of points A and B respectively.
Let a1, b1, c1, and a2, b2, c2 be the direction ratios of vectors b1 and b2 respectively. Then
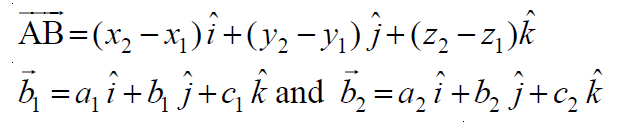
The given lines are coplanar if and only if:
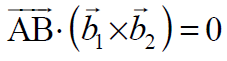
In Cartesian Form it can be expressed as:
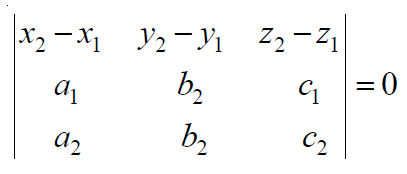
Therefore, for both type of forms needs a position vector a1 and a2 in input as (x1, y1, z1) and (x2, y2, z2) respectively and direction ratios of vectors b1 and b2 as (a1, b1, c1) and (a2, b2, c2) respectively.
Follow the steps below to solve the problem:
- Initialize a 3 X 3 matrix to store the elements of the Determinant shown above.
- Calculate the cross product of b2 and b1 and the dot product of (a2 – a1).
- If the value of the Determinant is 0, the lines are coplanar. Otherwise, they are non-coplanar.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
int det(int d[][3])
{
int Sum = d[0][0] * ((d[1][1] * d[2][2]) - (d[2][1] * d[1][2]));
Sum -= d[0][1] * ((d[1][0] * d[2][2]) - (d[1][2] * d[2][0]));
Sum += d[0][2] * ((d[0][1] * d[1][2]) -(d[0][2] * d[1][1]));
return Sum;
}
int main()
{
int x1 = -3, y1 = 1, z1 = 5;
int a1 = -3, b1 = 1, c1 = 5;
int x2 = -1, y2 = 2, z2 = 5;
int a2 = -1, b2 = 2, c2 = 5;
int det_list[3][3] = { {x2 - x1, y2 - y1, z2 - z1},
{a1, b1, c1}, {a2, b2, c2}};
if(det(det_list) == 0)
{
cout << "Lines are coplanar" << endl;
}
else
{
cout << "Lines are non coplanar" << endl;
}
return 0;
}
|
Java
import java.io.*;
class GFG{
static int det(int[][] d)
{
int Sum = d[0][0] * ((d[1][1] * d[2][2]) -
(d[2][1] * d[1][2]));
Sum -= d[0][1] * ((d[1][0] * d[2][2]) -
(d[1][2] * d[2][0]));
Sum += d[0][2] * ((d[0][1] * d[1][2]) -
(d[0][2] * d[1][1]));
return Sum;
}
public static void main (String[] args)
{
int x1 = -3, y1 = 1, z1 = 5;
int a1 = -3, b1 = 1, c1 = 5;
int x2 = -1, y2 = 2, z2 = 5;
int a2 = -1, b2 = 2, c2 = 5;
int[][] det_list = { {x2 - x1, y2 - y1, z2 - z1},
{a1, b1, c1}, {a2, b2, c2}};
if(det(det_list) == 0)
System.out.print("Lines are coplanar");
else
System.out.print("Lines are non coplanar");
}
}
|
Python3
def det(d):
Sum = d[0][0] * ((d[1][1] * d[2][2])
- (d[2][1] * d[1][2]))
Sum -= d[0][1] * ((d[1][0] * d[2][2])
- (d[1][2] * d[2][0]))
Sum += d[0][2] * ((d[0][1] * d[1][2])
- (d[0][2] * d[1][1]))
return Sum
if __name__ == '__main__':
x1, y1, z1 = -3, 1, 5
a1, b1, c1 = -3, 1, 5
x2, y2, z2 = -1, 2, 5
a2, b2, c2 = -1, 2, 5
det_list = [[x2-x1, y2-y1, z2-z1],
[a1, b1, c1], [a2, b2, c2]]
if(det(det_list) == 0):
print("Lines are coplanar")
else:
print("Lines are non coplanar")
|
C#
using System;
class GFG{
static int det(int[,] d)
{
int Sum = d[0, 0] * ((d[1, 1] * d[2, 2]) -
(d[2, 1] * d[1, 2]));
Sum -= d[0, 1] * ((d[1, 0] * d[2, 2]) -
(d[1, 2] * d[2, 0]));
Sum += d[0, 2] * ((d[0, 1] * d[1, 2]) -
(d[0, 2] * d[1, 1]));
return Sum;
}
public static void Main()
{
int x1 = -3, y1 = 1, z1 = 5;
int a1 = -3, b1 = 1, c1 = 5;
int x2 = -1, y2 = 2, z2 = 5;
int a2 = -1, b2 = 2, c2 = 5;
int[,] det_list = { {x2 - x1, y2 - y1, z2 - z1},
{a1, b1, c1}, {a2, b2, c2}};
if (det(det_list) == 0)
Console.Write("Lines are coplanar");
else
Console.Write("Lines are non coplanar");
}
}
|
Javascript
<script>
function det(d)
{
let Sum = d[0][0] * ((d[1][1] * d[2][2]) -
(d[2][1] * d[1][2]));
Sum -= d[0][1] * ((d[1][0] * d[2][2]) -
(d[1][2] * d[2][0]));
Sum += d[0][2] * ((d[0][1] * d[1][2]) -
(d[0][2] * d[1][1]));
return Sum;
}
let x1 = -3, y1 = 1, z1 = 5;
let a1 = -3, b1 = 1, c1 = 5;
let x2 = -1, y2 = 2, z2 = 5;
let a2 = -1, b2 = 2, c2 = 5;
let det_list = [[x2 - x1, y2 - y1, z2 - z1],
[a1, b1, c1], [a2, b2, c2]];
if(det(det_list) == 0)
document.write("Lines are coplanar");
else
document.write("Lines are non coplanar");
</script>
|
Output:
Lines are coplanar
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...