Find whether only two parallel lines contain all coordinates points or not

Difficulty Level : Hard
Last Updated : 29 Apr, 2021

Given an array that represents the y coordinates of a set of points on a coordinate plane, where (i, arr[i]) represent a single point. Find whether it is possible to draw a pair of parallel lines that includes all the coordinate points given and also both lines must contain a point. Print 1 for possible and 0 if not possible.

Examples:

Input: arr[] = {1, 4, 3, 6, 5};
Output: 1
(1, 1), (3, 3) and (5, 5) lie on one line
where as (2, 4) and (4, 6) lie on another line.
Input: arr[] = {2, 4, 3, 6, 5};
Output: 0
Minimum 3 lines needed to cover all points.

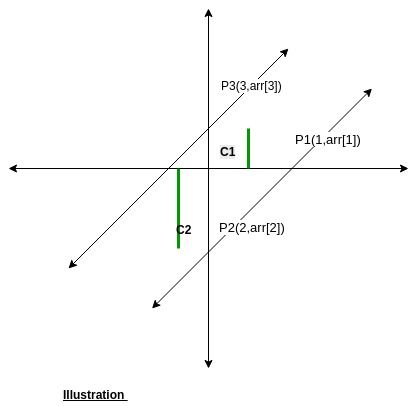
Approach: The slope of a line made by points (x1, y1) and (x2, y2) is y2-y2/x2-x1. As the given array consists of coordinates of points as (i, arr[i]). So, (arr[2]-arr[1]) / (2-1) is slope of line made by (1, arr[i]) and (2, arr[2]). Take in consideration of only three points say P0(0, arr[0]), P1(1, arr[1]), and P2(2, arr[2]) as the requirement is of only two parallel lines this is mandatory that two of these three points lie on the same line. So, three possible cases are:

P0 and P1 are on the same line hence their slope will be arr[1]-arr[0]
P1 and P2 are on the same line hence their slope will be arr[2]-arr[1]
P0 and P2 are on the same line hence their slope will be arr[2]-arr[0]/2

Take one out of three cases, say P0 and P1 lie on the same line, in this case, let m=arr[1]-arr[0] is our slope. For the general point in the array (i, arr[i]) the equation of the line is:

=> (y-y1) = m (x-x1)
=> y-arr[i] = m (x-i)
=> y-mx = arr[i] - mi

Now, as y-mx=c is general equation of straight line here c = arr[i] -mi. Now, if the solution will be possible for a given array then we must have exactly two intercepts (c).
So, if two distinct intercepts exist for any of the above-mentioned three possible, the required solution is possible and print 1 else 0.

Below is the implementation of the above approach:

C++

// C++ implementation of the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Find if slope is good with only two intercept
bool isSlopeGood(double slope, int arr[], int n)
{
    set<double> setOfLines;
    for (int i = 0; i < n; i++)
        setOfLines.insert(arr[i] - slope * (i));
 
    // if set of lines have only two distinct intercept
    return setOfLines.size() == 2;
}
 
// Function to check if required solution exist
bool checkForParallel(int arr[], int n)
{
    // check the result by processing
    // the slope by starting three points
    bool slope1 = isSlopeGood(arr[1] - arr[0], arr, n);
    bool slope2 = isSlopeGood(arr[2] - arr[1], arr, n);
    bool slope3 = isSlopeGood((arr[2] - arr[0]) / 2, arr, n);
 
    return (slope1 || slope2 || slope3);
}
 
// Driver code
int main()
{
    int arr[] = { 1, 6, 3, 8, 5 };
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << (int)checkForParallel(arr, n);
 
    return 0;
}

Java

// Java implementation of the above approach
import java.util.*;
 
class GfG
{
 
// Find if slope is good
// with only two intercept
static boolean isSlopeGood(double slope,
                        int arr[], int n)
{
    Set<Double> setOfLines = new HashSet<Double> ();
    for (int i = 0; i < n; i++)
        setOfLines.add(arr[i] - slope * (i));
 
    // if set of lines have only two distinct intercept
    return setOfLines.size() == 2;
}
 
// Function to check if required solution exist
static boolean checkForParallel(int arr[], int n)
{
    // check the result by processing
    // the slope by starting three points
    boolean slope1 = isSlopeGood(arr[1] - arr[0], arr, n);
    boolean slope2 = isSlopeGood(arr[2] - arr[1], arr, n);
    boolean slope3 = isSlopeGood((arr[2] - arr[0]) / 2, arr, n);
 
    return (slope1 == true || slope2 == true || slope3 == true);
}
 
// Driver code
public static void main(String[] args)
{
    int arr[] = { 1, 6, 3, 8, 5 };
    int n = arr.length;
    if(checkForParallel(arr, n) == true)
    System.out.println("1");
    else
    System.out.println("0");
}
}
 
// This code is contributed by Prerna Saini.

Python3

# Python3 implementation of the
# above approach
 
# Find if slope is good with only
# two intercept
def isSlopeGood(slope, arr, n):
 
    setOfLines = dict()
    for i in range(n):
        setOfLines[arr[i] - slope * (i)] = 1
 
    # if set of lines have only
    # two distinct intercept
    return len(setOfLines) == 2
 
# Function to check if required solution exist
def checkForParallel(arr, n):
     
    # check the result by processing
    # the slope by starting three points
    slope1 = isSlopeGood(arr[1] - arr[0], arr, n)
    slope2 = isSlopeGood(arr[2] - arr[1], arr, n)
    slope3 = isSlopeGood((arr[2] - arr[0]) // 2, arr, n)
 
    return (slope1 or slope2 or slope3)
 
# Driver code
arr = [1, 6, 3, 8, 5 ]
n = len(arr)
if checkForParallel(arr, n):
    print(1)
else:
    print(0)
     
# This code is contributed by Mohit Kumar   

C#

// C# implementation of the above approach
using System;
using System.Collections.Generic;
 
class GfG
{
 
// Find if slope is good
// with only two intercept
static bool isSlopeGood(double slope,
                        int []arr, int n)
{
 
    HashSet<Double> setOfLines = new HashSet<Double> ();
    for (int i = 0; i < n; i++)
        setOfLines.Add(arr[i] - slope * (i));
 
    // if set of lines have only two distinct intercept
    return setOfLines.Count == 2;
}
 
// Function to check if required solution exist
static bool checkForParallel(int []arr, int n)
{
    // check the result by processing
    // the slope by starting three points
    bool slope1 = isSlopeGood(arr[1] - arr[0], arr, n);
    bool slope2 = isSlopeGood(arr[2] - arr[1], arr, n);
    bool slope3 = isSlopeGood((arr[2] - arr[0]) / 2, arr, n);
 
    return (slope1 == true || slope2 == true || slope3 == true);
}
 
// Driver code
public static void Main()
{
    int []arr = { 1, 6, 3, 8, 5 };
    int n = arr.Length;
    if(checkForParallel(arr, n) == true)
        Console.WriteLine("1");
    else
        Console.WriteLine("0");
}
}
 
// This code is contributed by Ryuga.

PHP

<?php
// PHP implementation of the above approach
 
// Find if slope is good with only
// two intercept
function isSlopeGood($slope, $arr, $n)
{
    $setOfLines = array_fill(0, max($arr) * $n, 0);
    for ($i = 0; $i < $n; $i++)
        $setOfLines[$arr[$i] - $slope * $i] = 1;
    $setOfLines = array_unique($setOfLines);
     
    // if set of lines have only two
    // distinct intercept
    return (count($setOfLines) == 2);
}
 
// Function to check if required
// solution exist
function checkForParallel($arr, $n)
{
    // check the result by processing
    // the slope by starting three points
    $slope1 = isSlopeGood($arr[1] - $arr[0],
                                    $arr, $n);
    $slope2 = isSlopeGood($arr[2] - $arr[1],
                                    $arr, $n);
    $slope3 = isSlopeGood((int)(($arr[2] -
                                 $arr[0]) / 2),
                                 $arr, $n);
 
    return ($slope1 || $slope2 || $slope3);
}
 
// Driver code
$arr = array( 1, 6, 3, 8, 5 );
$n = count($arr);
echo (int)checkForParallel($arr, $n) . "\n";
 
// This code is contributed by mits
?>

Javascript

<script>
 
// Javascript implementation of the above approach
 
// Find if slope is good with only two intercept
function isSlopeGood(slope, arr, n)
{
    var setOfLines = new Set();
    for (var i = 0; i < n; i++)
        setOfLines.add(arr[i] - slope * (i));
 
    // if set of lines have only two distinct intercept
    return setOfLines.size == 2;
}
 
// Function to check if required solution exist
function checkForParallel(arr, n)
{
    // check the result by processing
    // the slope by starting three points
    var slope1 = isSlopeGood(arr[1] - arr[0], arr, n);
    var slope2 = isSlopeGood(arr[2] - arr[1], arr, n);
    var slope3 = isSlopeGood(parseInt((arr[2] - arr[0]) / 2), arr, n);
 
    if(slope1 || slope2 || slope3)
    {
        return 1;
    }
    return 0;
}
 
// Driver code
var arr = [ 1, 6, 3, 8, 5 ];
var n = arr.length;
document.write( checkForParallel(arr, n));
 
</script>

Output:

My Personal Notes

Related Articles

Table of Contents

Find whether only two parallel lines contain all coordinates points or not

C++

Java

Python3

C#

PHP

Javascript

Start Your Coding Journey Now!