Common prime factors of two numbers
Last Updated :
06 Jun, 2021
Given two integer 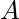 and
and 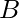 , the task is to find the common prime divisors of these numbers.
, the task is to find the common prime divisors of these numbers.
Examples:
Input: A = 6, B = 12
Output: 2 3
2 and 3 are the only common prime divisors of 6 and 12
Input: A = 4, B = 8
Output: 2
Naive Approach: Iterate from 1 to min(A, B) and check whether i is prime and a factor of both A and B, if yes then display the number.
Efficient Approach is to do following:
- Find Greatest Common Divisor (gcd) of the given numbers.
- Find prime factors of the GCD.
Efficient Approach for multiple queries: The above solution can be further optimized if there are multiple queries for common factors. The idea is based on Prime Factorization using Sieve O(log n) for multiple queries.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define MAXN 100001
bool prime[MAXN];
void SieveOfEratosthenes()
{
memset(prime, true, sizeof(prime));
prime[0] = false;
prime[1] = false;
for (int p = 2; p * p <= MAXN; p++) {
if (prime[p] == true) {
for (int i = p * p; i <= MAXN; i += p)
prime[i] = false;
}
}
}
void common_prime(int a, int b)
{
int gcd = __gcd(a, b);
for (int i = 2; i <= (gcd); i++) {
if (prime[i] && gcd % i == 0) {
cout << i << " ";
}
}
}
int main()
{
SieveOfEratosthenes();
int a = 6, b = 12;
common_prime(a, b);
return 0;
}
|
Java
class GFG {
static final int MAXN = 100001;
static boolean prime[] = new boolean[MAXN];
static void SieveOfEratosthenes()
{
for(int i = 0;i<prime.length;i++)
prime[i]=true;
prime[0] = false;
prime[1] = false;
for (int p = 2; p * p < MAXN; p++) {
if (prime[p] == true) {
for (int i = p * p; i < MAXN; i += p)
prime[i] = false;
}
}
}
static void common_prime(int a, int b)
{
int gcd = (int) __gcd(a, b);
for (int i = 2; i <= (gcd); i++) {
if (prime[i] && gcd % i == 0) {
System.out.print(i + " ");
}
}
}
static long __gcd(long a, long b)
{
if (a == 0)
return b;
return __gcd(b % a, a);
}
public static void main(String[] args) {
SieveOfEratosthenes();
int a = 6, b = 12;
common_prime(a, b);
}
}
|
Python3
from math import gcd, sqrt
prime = [True] * 100001
def SieveOfEratosthenes() :
prime[0] = False
prime[1] = False
for p in range(2, int(sqrt(100001)) + 1) :
if prime[p] == True :
for i in range(p**2, 100001, p) :
prime[i] = False
def common_prime(a, b) :
__gcd = gcd(a, b)
for i in range(2, __gcd + 1) :
if prime[i] and __gcd % i == 0 :
print(i, end = " ")
if __name__ == "__main__" :
SieveOfEratosthenes()
a, b = 6, 12
common_prime(a, b)
|
C#
using System;
public class GFG {
static bool []prime = new bool[100001];
static void SieveOfEratosthenes()
{
for(int i = 0;i<prime.Length;i++)
prime[i]=true;
prime[0] = false;
prime[1] = false;
for (int p = 2; p * p < 100001; p++) {
if (prime[p] == true) {
for (int i = p * p; i < 100001; i += p)
prime[i] = false;
}
}
}
static void common_prime(int a, int b)
{
int gcd = (int) __gcd(a, b);
for (int i = 2; i <= (gcd); i++) {
if (prime[i] && gcd % i == 0) {
Console.Write(i + " ");
}
}
}
static long __gcd(long a, long b)
{
if (a == 0)
return b;
return __gcd(b % a, a);
}
public static void Main() {
SieveOfEratosthenes();
int a = 6, b = 12;
common_prime(a, b);
}
}
|
Javascript
<script>
MAXN = parseInt(100001);
prime = new Array(MAXN);
function __gcd(a, b)
{
if (a == 0)
return b;
return __gcd(b % a, a);
}
function SieveOfEratosthenes()
{
prime.fill(true);
prime[0] = false;
prime[1] = false;
for (var p = 2; p * p <= MAXN; p++) {
if (prime[p] == true) {
for (var i = p * p; i <= MAXN; i += p)
prime[i] = false;
}
}
}
function common_prime( a, b)
{
var gcd = __gcd(a, b);
for (var i = 2; i <= (gcd); i++) {
if (prime[i] && gcd % i == 0) {
document.write( i + " ");
}
}
}
SieveOfEratosthenes();
var a = 6, b = 12;
common_prime(a, b);
</script>
|
Share your thoughts in the comments
Please Login to comment...