Coalitional Game theory

Coalitional game theory has now become the dominant group of game theory which makes sure of the group preference rather than individual actions. It focuses more on the group than an individual agent as the basic modelling unit. More precisely, we will still be modelling the individual preferences of agents, but definitely not their possible actions. Instead, we would be taking a deep interest in the coarser model of the capabilities of different groups.

Coalitional Game theory

Coalitional Game theory focuses on the achievement of groups of agents, rather in an individualistic sense. Given a set of agents, coalitional game theory defines how well each coalition or group can perform and do for itself. In a broader view, it looks for the achievements of the group of agents rather than the choices of the individuals within that particular coalition or their manner of coordination among each other.

In such a case, the payoffs to a coalition may be freely redistributed among its members since we would be looking at the coalition as a whole. Such transferable utility is assumed to be satisfied whenever there is a universal currency used for exchange in the system.

Preliminaries

A coalitional game (N, v) is a set of players N, with let’s say, coalition S which is a group of cooperating players (subset of N).

The payoff v(S) which is the worth of a coalition v, is a real number representing the gain from the coalition S in the game (N, v). Further, v(N) is the worth of forming a coalition of all users, which is said as a grand coalition.

The user payoff x_i is the portion of v(S) that is received by a player i in coalition S.

Coalitional Game Utility

Transferable Utility (TU)

To proceed with Transferable Utility, we follow some basic assumptions.

• The payoffs to the coalition need to be freely distributed among its members, i.e., v(S) can be distributed arbitrarily among the players in the coalition.
• The player should be satisfied whenever there is a universal currency used for the purpose of exchange.
• Each coalition can possibly be assigned a single value as its payoff.

A coalitional game with transferable utility can thus be considered as a pair (N, v), where

• N being the finite set of players, and
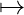
• v : 2^N , which associates with each coalition S 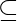N a real-valued payoff v(S) that the coalition’s members can distribute among themselves.

We normally assume v(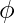) = 0.

Based on the distribution of payoff among its members by the coalition, the coalition of all the agents in N can be said as the Grand Coalition.

Non-Transferable Utility (NTU)

In case of non-transferable utility, we believe that the payoff of the player in the coalition is pre-determined and so the value of the coalition cannot be described by a function.

Thus, for non-transferable utility, we have

v(S) 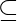^|S|, where v(S) is a set of payoff vectors that the players in the coalition S can achieve.

Example to build coalitional game

Case I

Consider a region with multiple political parties in space, say, A, B, C and D with 45, 25, 15 and 15 members, respectively. They are to vote on particular bill which will decide as to how much amount will they be receiving for the following year. To pass any bill the required majority is of 51 members. They can follow one among the below two approaches.

1. The bill is passed by more than 51 members, thus they receive the amount as was mentioned.
2. The bill doesn’t gets the required majority and thus the party are left with zero to spend.

In such a game, there is a set of coalitions W 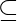2^N as the winning coalitions which are sufficient to pass the bill, where N being the set of agents.

To each coalition S 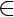W, we would be assigning v(S) = 1 and the others as v(S) = 0.

Case II

Consider a group of cities requiring an airport. They have two choices with them.

1. All the cities can have their individual airport. For this, they will have to incur the expenses their own.
2. The cities can built a common airport sharing the cost. This will depend on the largest aircraft that the runway can accommodate.

This scenario can be modeled as a coalitional game (N, v), where

• N is the group of cities, and
• v(S) is the sum of the costs of building the runway for each city in S minus the cost of largest runway required by any city in S.

Classes of coalitional game

Superadditive games

Superadditivity is said when the coalitions can work without any sort of interference. This includes both within the group and outside of it.

In such a case, the value of any two coalitions will be no less than the sum of their individual values and the grand coalition will be having the highest payoff.

A game G = (N, v) is said as superadditive, if for all S, T 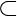N, if

S T = 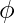, then

v(S T) v(S) + v(T)

Convex games

Convex games are too rare in practice and is a stronger condition than superadditivity.

A game G = (N, v) is said as convex, if for all S, T 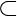N,

v(S T) v(S) + v(T) – v(S T)

Conclusion

Coalitional game theory being a high-level approach describes only the structure, strategies and the payoffs of coalitions. This can be analyzed through the approach of non-cooperative game theory provided all the assumptions are made as to encompass the possible actions each player can move because of the presence of external enforcement. In cases where the resulting model will be of too high complexity, coalitional game theory can provide a simplified approach without having to make any assumption on the bargaining powers.