Rough Set Theory | An Introduction
Last Updated :
06 Jul, 2022
The notion of Rough sets was introduced by Z Pawlak in his seminal paper of 1982 (Pawlak 1982). It is a formal theory derived from fundamental research on logical properties of information systems. Rough set theory has been a methodology of database mining or knowledge discovery in relational databases. In its abstract form, it is a new area of uncertainty mathematics closely related to fuzzy theory. We can use rough set approach to discover structural relationship within imprecise and noisy data. Rough sets and fuzzy sets are complementary generalizations of classical sets. The approximation spaces of rough set theory are sets with multiple memberships, while fuzzy sets are concerned with partial memberships. The rapid development of these two approaches provides a basis for “soft computing, ” initiated by Lotfi A. Zadeh. Soft Computing includes along with rough sets, at least fuzzy logic, neural networks, probabilistic reasoning, belief networks, machine learning, evolutionary computing, and chaos theory.
Basic problems in data analysis solved by Rough Set:
- Characterization of a set of objects in terms of attribute values.
- Finding dependency between the attributes.
- Reduction of superfluous attributes.
- Finding the most significant attributes.
- Decision rule generation.
Goals of Rough Set Theory –
- The main goal of the rough set analysis is the induction of (learning) approximations of concepts. Rough sets constitute a sound basis for KDD. It offers mathematical tools to discover patterns hidden in data.
- It can be used for feature selection, feature extraction, data reduction, decision rule generation, and pattern extraction (templates, association rules) etc.
- Identifies partial or total dependencies in data, eliminates redundant data, gives approach to null values, missing data, dynamic data and others.
Information system –
In Rough Set, data model information is stored in a table. Each row (tuples) represents a fact or an object. Often the facts are not consistent with each other. In Rough Set terminology a data table is called an Information System. Thus, the information table represents input data, gathered from any domain.

Note: Rows of a table are called examples(objects, entities). Information system is a pair (U, A), U is a non-empty finite set of objects and A is a non-empty finite set of attributes. The elements of A are called conditional attributes. An Information table sometimes called decision table when it contains decision attribute/attributes. Decision system is a pair of (U, A union {d}), where d is decision attribute (instead of one we can consider more decision attributes).

Indiscernibility –
Tables may contain many objects having the same features. A way of reducing table size is to store only one representative object for every set of objects with same features. These objects are called indiscernible objects or tuples. With any P subset A there is an associated equivalence relation IND(P): Where IND(P) is called indiscernibility of relation. Here x and y are indiscernible from each other by attribute P.
Where IND(P) is called indiscernibility of relation. Here x and y are indiscernible from each other by attribute P.  In above example,
In above example,
IND({p1}) = {{O1, O2}, {O3, O5, O7, O9, O10}, {O4, O6, O8}} O1 and O2 are characterized by the same values of attribute p1 and the value is 1. O3, O5, O7, O9, O10 are characterized by the same value of attribute p1 and the value is 2. O4, O6, O8 are characterized by the same value of attribute p1 and the value is 0.
The indiscernibility relation is an equivalence relation. Sets that are indiscernible are called elementary sets.
Approximations –
It is a formal approximation of a crisp set defined by its two approximations – Upper approximation and Lower approximation.
- Upper approximation is the set of objects which possibly belong to the target set.

- Lower approximation is the set of objects that positively belong to the target set.

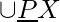 represents the positive region which contains the objects definitely belonging to the target set X.
represents the positive region which contains the objects definitely belonging to the target set X.  represents the negative region which contains the objects that can be definitely ruled out as a member of the target set X.
represents the negative region which contains the objects that can be definitely ruled out as a member of the target set X. 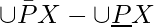 represents the boundary region which contains the objects that may or may not belong to the target set X.
represents the boundary region which contains the objects that may or may not belong to the target set X.
A set is said to be rough if its boundary region is non-empty, otherwise the set is crisp. 
Let’s discuss an example. the previous table is taken as information table. 
References: http://zsi.tech.us.edu.pl/~nowak/bien/w2.pdf https://www.sciencedirect.com/science/article/pii/S2468232216300786 https://www.mimuw.edu.pl/~son/datamining/RSDM/Intro.pdf
Share your thoughts in the comments
Please Login to comment...