Class 8 NCERT Solutions- Chapter 3 Understanding Quadrilaterals – Exercise 3.3
Last Updated :
21 Mar, 2024
Question 1. Given a parallelogram ABCD. Complete each statement along with the definition or property used.
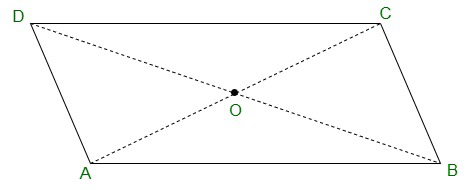
(i) AD = ……
(ii) ∠DCB = ……
(iii) OC = ……
(iv) m ∠DAB + m ∠CDA = ……
Solution:
(i) AD = BC {Opposite sides of a parallelogram are equal}
(ii) ∠DCB = ∠DAB {Opposite angles of a parallelogram are equal}
(iii) OC = OA {Diagonals of a parallelogram are equal}
(iv) m ∠DAB + m ∠CDA = 180°
Question 2. Consider the following parallelograms. Find the values of the unknown x, y, z
Solution:
(i)

y = 100° {opposite angles of a parallelogram}
x + 100° = 180° {Adjacent angles of a parallelogram}
⇒ x = 180° – 100°
⇒ x = 80°
x = z = 80° {opposite angles of a parallelogram}
Therefore,
x = 80°, y = 100° and z = 80°
(ii)

50° + x = 180°
⇒ x = 180° – 50° = 130° {Adjacent angles of a parallelogram}
⇒ x = y = 130° {opposite angles of a parallelogram}
⇒ x = z = 130° {corresponding angle}
(iii)

x = 90° {vertical opposite angles}
x + y + 30° = 180° {angle sum property of a triangle}
⇒ 90° + y + 30° = 180°
⇒ y = 180° – 120° = 60°
also, y = z = 60° {alternate angles}
(iv)

z = 80° {corresponding angle}
z = y = 80° {alternate angles}
x + y = 180° {adjacent angles}
⇒ x + 80° = 180°
⇒ x = 180° – 80° = 100°
(v)

y = 112° {opposite angles of a parallelogram}
x = 180° – (y + 40°) {angle sum property of a triangle}
x = 28°
z = 28° {alternate angles}
Question 3. Can a quadrilateral ABCD be a parallelogram if
(i) ∠D + ∠B = 180°?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
(iii)∠A = 70° and ∠C = 65°?
Solution:
(i) Yes,
The quadrilateral ABCD be a parallelogram if ∠D + ∠B = 180°,
it should also fulfilled some conditions which are:
(a) The sum of the adjacent angles should be 180°.
(b) Opposite angles must be equal.
(ii) No, opposite sides should be of the same length.
Here, AD ≠ BC
(iii) No, opposite angles should be of same measures.
Here, ∠A ≠ ∠C
Question 4. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
Solution:

ABCD is a figure of quadrilateral which is not a parallelogram but has exactly two opposite angles
that is ∠B = ∠D of equal measure. It is not a parallelogram because ∠A ≠ ∠C.
Question 5. The measures of two adjacent angles of a parallelogram are in the ratio 3:2. Find the measure of each of the angles of the parallelogram.
Solution:
Let the measures of two adjacent angles ∠A and ∠B be 3x and 2x respectively in parallelogram ABCD.
∠A + ∠B = 180°
⇒ 3x + 2x = 180°
⇒ 5x = 180°
⇒ x = 36°
As we know opposite sides of a parallelogram are equal.
∠A = ∠C = 3x = 3 × 36° = 108°
∠B = ∠D = 2x = 2 × 36° = 72°
Question 6. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Solution:
Let ABCD be a parallelogram.
The sum of adjacent angles of a parallelogram = 180°
∠A + ∠B = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°
also,
90° + ∠B = 180°
⇒ ∠B = 180° – 90° = 90°
∠A = ∠C = 90°
∠B = ∠D = 90°
Question 7. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y, and z. State the properties you use to find them.

Solution:
y = 40° {alternate interior angle}
∠P = 70° {alternate interior angle}
∠P = ∠H = 70° {opposite angles of a parallelogram}
z = ∠H – 40°= 70° – 40° = 30°
∠H + x = 180°
⇒ 70° + x = 180°
⇒ x = 180° – 70° = 110°
Question 8. The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)
Solution:
(i)

SG = NU and SN = GU {opposite sides of a parallelogram are equal}
3x = 18
x = 18/3
⇒ x =6
3y – 1 = 26 and,
⇒ 3y = 26 + 1
⇒ y = 27/3=9
x = 6 and y = 9
(ii)

20 = y + 7 and 16 = x + y {diagonals of a parallelogram bisect each other}
y + 7 = 20
⇒ y = 20 – 7 = 13 and,
x + y = 16
⇒ x + 13 = 16
⇒ x = 16 – 13 = 3
x = 3 and y = 13
Question 9. In the above figure, both RISK and CLUE are parallelograms. Find the value of x.

Solution:
∠K + ∠R = 180° {adjacent angles of a parallelogram are supplementary}
⇒ 120° + ∠R = 180°
⇒ ∠R = 180° – 120° = 60°
also, ∠R = ∠SIL {corresponding angles}
⇒ ∠SIL = 60°
also,
∠ECR = ∠L = 70° {corresponding angles}
x + 60° + 70° = 180° {angle sum of a triangle}
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
Question 10. Explain how this figure is a trapezium. Which of its two sides is parallel? (Figure)

Solution:
When a transversal line intersects two lines in such a way that the sum of the adjacent angles on the same side of transversal is 180° then, the lines are parallel to each other.
Here we have, ∠M + ∠L = 100° + 80° = 180°
Hence, MN || LK
As the quadrilateral KLMN has one pair of parallel line therefore it is a trapezium.
MN and LK are parallel lines.
Question 11. Find m∠C in Figure if AB || DC?

Solution:
m∠C + m∠B = 180° {angles on the same side of transversal}
⇒ m∠C + 120° = 180°
⇒ m∠C = 180° − 120° = 60°
Question 12. Find the measure of ∠P and ∠S if SP || RQ ? in Figure. (If you find m∠R, is there more than one method to find m∠P?)

Solution:
∠P + ∠Q = 180° {angles on the same side of transversal}
⇒ ∠P + 130° = 180°
⇒ ∠P = 180° – 130° = 50°
also,
∠R + ∠S = 180° {angles on the same side of transversal}
⇒ 90° + ∠S = 180°
⇒ ∠S = 180° – 90° = 90°
Hence, ∠P = 50° and ∠S = 90°
Yes, there are more than one method to find m∠P.
PQRS is a quadrilateral. Sum of measures of all angles of a quadrilateral is 360°.
Thus, as we know the measurement of ∠Q, ∠R and ∠S.
∠Q = 130°, ∠R = 90° and ∠S = 90°
∠P + 130° + 90° + 90° = 360°
⇒ ∠P + 310° = 360°
⇒ ∠P = 360° – 310° = 50°
Share your thoughts in the comments
Please Login to comment...