To check whether a large number is divisible by 7
Last Updated :
14 Aug, 2023
You are given an n-digit large number, you have to check whether it is divisible by 7.
A (r+1)-digit integer n whose digital form is (ar ar-1 ar-2….a2 a1 a0) is divisible by 7 if and only if the alternate series of numbers (a2 a1 a0) – (a5 a4 a3) + (a8 a7 a6) – … is divisible by 7.
The triplets of digits within parenthesis represent a 3-digit number in digital form.
The given number n can be written as a sum of powers of 1000 as follows.
n= (a2 a1 a0) + (a5 a4 a3)*1000 + (a8 a7 a6)*(1000*1000) +….
As 1000 = (-1)(mod 7), 1000 as per congruence relation.
For a positive integer n, two numbers a and b are said to be congruent modulo n, if their difference
(a – b) is an integer multiple of n (that is, if there is an integer k such that a – b = kn). This congruence relation is typically considered when a and b are integers, and is denoted
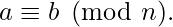
Hence we can write:
n = { (a2a1a0) + (a5a4a3)* (-1) + (a8a7a6)* (-1)*(-1)+…..}(mod 7),
Thus n is divisible by 7 if and if only if the series is divisible by 7.
Examples:
Input : 8955795758
Output : Divisible by 7
Explanation:
We express the number in terms of triplets
of digits as follows.
(008)(955)(795)(758)
Now, 758- 795 + 955 - 8 = 910, which is
divisible by 7
Input : 100000000000
Output : Not Divisible by 7
Explanation:
We express the number in terms of triplets
of digits as follows.
(100)(000)(000)(000)
Now, 000- 000 + 000 - 100 = -100, which is
not divisible by 7
Note that the number of digits in n may not be multiple of 3. In that case, we pass zero(s) on the left side of the remaining digits(s) after taking out all the triplets (from the right side of n) to form the last triplet.
A simple and efficient method is to take input in form of a string (make its length in form of 3*m by adding 0 to left of the number if required) and then you have to add the digits in blocks of three from the right to left until it becomes a 3 digit number to form an alternate series and check whether the series is divisible by 7 or not.
Here the program implementation to check the divisibility of 7 is done.
C++
#include<bits/stdc++.h>
using namespace std;
int isdivisible7(string num)
{
int n = num.length(), gSum=0;
if (n == 0)
return 1;
if (n % 3 == 1) {
num="00" + num;
n += 2;
}
else if (n % 3 == 2) {
num= "0" + num;
n++;
}
int i, GSum = 0, p = 1;
for (i = n - 1; i >= 0; i--) {
int group = 0;
group += num[i--] - '0';
group += (num[i--] - '0') * 10;
group += (num[i] - '0') * 100;
gSum = gSum + group * p;
p *= (-1);
}
return (gSum % 7 == 0);
}
int main()
{
string num= "8955795758";
if (isdivisible7(num))
cout << "Divisible by 7";
else
cout << "Not Divisible by 7";
return 0;
}
|
C
#include <stdio.h>
#include <string.h>
int isdivisible7(char num[])
{
int n = strlen(num), gSum=0;
char final[n+3];
if (n == 0 && num[0] == '\n')
return 1;
if (n % 3 == 1) {
final[0]='0';
final[1]='0';
strcat(final,num);
n += 2;
}
else if (n % 3 == 2) {
final[0]='0';
strcat(final,num);
n++;
}
int i, GSum = 0, p = 1;
for (i = n - 1; i >= 0; i--) {
int group = 0;
group += final[i--] - '0';
group += (final[i--] - '0') * 10;
group += (final[i] - '0') * 100;
gSum = gSum + group * p;
p *= (-1);
}
return (gSum % 7 == 0);
}
int main()
{
char num[] = "8955795758";
if (isdivisible7(num))
printf("Divisible by 7");
else
printf("Not Divisible by 7");
return 0;
}
|
Java
class Test {
static boolean isDivisible7(String num)
{
int n = num.length();
if (n == 0 && num.charAt(0) == '0')
return true;
if (n % 3 == 1)
num = "00" + num;
if (n % 3 == 2)
num = "0" + num;
n = num.length();
int gSum = 0, p = 1;
for (int i = n - 1; i >= 0; i--) {
int group = 0;
group += num.charAt(i--) - '0';
group += (num.charAt(i--) - '0') * 10;
group += (num.charAt(i) - '0') * 100;
gSum = gSum + group * p;
p = p * -1;
}
return (gSum % 7 == 0);
}
public static void main(String args[])
{
String num = "8955795758";
System.out.println(isDivisible7(num) ? "Divisible by 7" : "Not Divisible by 7");
}
}
|
Python3
def isdivisible7(num):
n = len(num)
if (n == 0 and num[0] == '\n'):
return 1
if (n % 3 == 1) :
num = "00" + str(num)
n += 2
elif (n % 3 == 2) :
num = "0" + str(num)
n += 1
GSum = 0
p = 1
i = n-1
while i>=0 :
group = 0
group += ord(num[i]) - ord('0')
i -= 1
group += (ord(num[i]) - ord('0')) * 10
i -= 1
group += (ord(num[i]) - ord('0')) * 100
GSum = GSum + group * p
p *= (-1)
i -= 1
return (GSum % 7 == 0)
if __name__ == "__main__":
num = "8955795758"
if (isdivisible7(num)):
print("Divisible by 7")
else :
print("Not Divisible by 7")
|
C#
using System;
class GFG {
static bool isDivisible7(String num)
{
int n = num.Length;
if (n == 0 && num[0] == '0')
return true;
if (n % 3 == 1)
num = "00" + num;
if (n % 3 == 2)
num = "0" + num;
n = num.Length;
int gSum = 0, p = 1;
for (int i = n - 1; i >= 0; i--) {
int group = 0;
group += num[i--] - '0';
group += (num[i--] - '0') * 10;
group += (num[i] - '0') * 100;
gSum = gSum + group * p;
p = p * -1;
}
return (gSum % 7 == 0);
}
static public void Main()
{
String num = "8955795758";
Console.WriteLine(isDivisible7(num) ? "Divisible by 7" : "Not Divisible by 7");
}
}
|
Javascript
<script>
function isDivisible7(num)
{
let n = num.length;
if (n == 0 && num[0] == '0')
return true;
if (n % 3 == 1)
num = "00" + num;
if (n % 3 == 2)
num = "0" + num;
n = num.length;
gSum = 0 ;
let p = 1;
for(let i = n - 1; i >= 0; i--)
{
group = 0;
group += num[i--] - '0';
group += (num[i--] - '0') * 10;
group += (num[i] - '0') * 100;
gSum = gSum + group * p;
p = p * -1;
}
return (gSum % 7 == 0);
}
let num = "8955795758";
document.write(isDivisible7(num) ?
"Divisible by 7" :
"Not Divisible by 7");
</script>
|
PHP
<?php
function isDivisible7($num)
{
$n = strlen($num) ;
if ($n == 0 && $num[0] == '0')
return true;
if ($n % 3 == 1)
$num = "00" . $num;
if ($n % 3 == 2)
$num = "0". $num;
$n = strlen($num);
$gSum = 0 ;
$p = 1;
for ($i = $n - 1; $i >= 0; $i--)
{
$group = 0;
$group += $num[$i--] - '0';
$group += ($num[$i--] - '0') * 10;
$group += ($num[$i] - '0') * 100;
$gSum = $gSum + $group * $p;
$p = $p * -1;
}
return ($gSum % 7 == 0);
}
$num = "8955795758";
echo (isDivisible7($num) ?
"Divisible by 7" :
"Not Divisible by 7");
?>
|
Time Complexity: O(n), where n is the number of digits in num.
Auxiliary Space: O(1)
Method 2: Checking given number is divisible by 7 or not by using modulo division operator “%”.
C++
#include <iostream>
using namespace std;
int main()
{
long long int n=100000000000;
if (n%7==0)
{
cout << "Yes";
}
else
{
cout << "No";
}
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG
{
public static void main(String[] args)
{
long n=100000000000L;
if ((n)%7==0)
{
System.out.println("Yes");
}
else
{
System.out.println("No");
}
}
}
|
Python3
n=100000000000
if int(n)%7==0:
print("Yes")
else:
print("No")
|
C#
using System;
public class GFG {
public static void Main()
{
long n=100000000000;
if (n%7==0)
{
Console.Write("Yes");
}
else
{
Console.Write("No");
}
}
}
|
Javascript
<script>
var n = 100000000000
if (n % 7 == 0)
document.write("Yes")
else
document.write("No")
</script>
|
PHP
<?php
$n=100000000000;
if ($n%7==0)
{
echo "Yes";
}
else
{
echo "No";
}
?>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Method 3: Checking given String(containing digits 0-9) is divisible by 7 or not by checking each character of the string and taking its modulo % .
Firstly we take first character of the String and take its modulo with 7 .
Then we add the remainder with the next character and take modulo of that and so.. on , until we reach the end of the string .
If at last we have remainder as 0 we get string divisible by 7 otherwise we get it as not divisible by 7 .
C++
#include <bits/stdc++.h>
using namespace std;
bool isDivisibleBySeven(string s)
{
int remainder = 0;
for (int i = 0; i < s.length(); i++) {
int digit = remainder * 10 + (s[i] - '0');
remainder = digit % 7;
}
return remainder == 0;
}
int main()
{
string s = "8955795758";
bool check = isDivisibleBySeven(s);
cout << ((check) ? "String is divisible by 7"
: "String is not divisible by 7");
return 0;
}
|
Java
import java.io.*;
import java.util.Scanner;
class GFG {
public boolean isDivisibleBySeven(String s)
{
int remainder = 0;
for (int i = 0; i < s.length(); i++) {
int digit
= remainder * 10 + (s.charAt(i) - '0');
remainder = digit % 7;
}
return remainder == 0;
}
public static void main(String[] args)
{
GFG obj = new GFG();
String s = "8955795758";
boolean check = obj.isDivisibleBySeven(s);
System.out.print(
(check) ? "String is divisible by 7"
: "String is not divisible by 7");
}
}
|
Python3
def isDivisibleBySeven(s):
remainder = 0
for i in range(len(s)):
digit = remainder * 10 + int(s[i]) - 0
remainder = digit % 7
return remainder == 0
s = "8955795758"
check = isDivisibleBySeven(s)
print("String is divisible by 7" if check else "String is not divisible by 7")
|
C#
using System;
public class GFG {
public bool isDivisibleBySeven(String s)
{
int remainder = 0;
for (int i = 0; i < s.Length; i++) {
int digit = remainder * 10 + (s[i] - '0');
remainder = digit % 7;
}
return remainder == 0;
}
static public void Main()
{
GFG obj = new GFG();
string s = "8955795758";
bool check = obj.isDivisibleBySeven(s);
Console.Write((check)
? "String is divisible by 7"
: "String is not divisible by 7");
}
}
|
Javascript
function isDivisibleBySeven(s) {
let remainder = 0;
for (let i = 0; i < s.length; i++) {
let digit = remainder * 10 + (s.charCodeAt(i) - '0'.charCodeAt(0));
remainder = digit % 7;
}
return remainder === 0;
}
let s = "8955795758";
let check = isDivisibleBySeven(s);
console.log(check ? "String is divisible by 7" : "String is not divisible by 7");
|
OutputString is divisible by 7
Time Complexity: O(n) , n being length of the input string .
Auxiliary Space: O(1)
Method 4:
We can use the following property to check whether a number is divisible by 7 or not:
- If we subtract twice the last digit of the number from the remaining prefix, the resulting number will be divisible by 7 if and only if the original number is divisible by 7.
We can repeatedly apply this property until we are left with a 2-digit number, and then check whether it is divisible by 7 or not.
Steps:
- Initialize the given number as n.
- While n is greater than or equal to 100, do the following:
a. Extract the last digit of n.
b. Update n as n // 10 – 2 * last_digit. - Check whether the remaining 2-digit number is divisible by 7 or not.
- If the remaining 2-digit number is divisible by 7, return “Divisible by 7”, otherwise return “Not divisible by 7”.
C++
#include <iostream>
using namespace std;
string is_divisible_by_7(long long n)
{
while (n >= 100) {
int last_digit = n % 10;
n = n / 10 - 2 * last_digit;
}
return (n % 7 == 0) ? "Divisible by 7"
: "Not divisible by 7";
}
int main()
{
long long number = 8955795758;
cout << is_divisible_by_7(number) << endl;
return 0;
}
|
Java
import java.util.*;
public class Main {
public static String isDivisibleBy7(long n)
{
while (n >= 100) {
int lastDigit = (int)(n % 10);
n = n / 10 - 2 * lastDigit;
}
return (n % 7 == 0) ? "Divisible by 7"
: "Not divisible by 7";
}
public static void main(String[] args)
{
long number = 8955795758L;
System.out.println(isDivisibleBy7(number));
}
}
|
Python3
def is_divisible_by_7(n):
while n >= 100:
last_digit = n % 10
n = n // 10 - 2 * last_digit
return "Divisible by 7" if n % 7 == 0 else "Not divisible by 7"
number = 8955795758
print(is_divisible_by_7(number))
|
C#
using System;
class GFG
{
static string IsDivisibleBy7(long n)
{
while (n >= 100)
{
int lastDigit = (int)(n % 10);
n = n / 10 - 2 * lastDigit;
}
return (n % 7 == 0) ? "Divisible by 7" : "Not divisible by 7";
}
static void Main(string[] args)
{
long number = 8955795758;
Console.WriteLine(IsDivisibleBy7(number));
}
}
|
Javascript
function isDivisibleBy7(n) {
while (n >= 100) {
var lastDigit = n % 10;
n = Math.floor(n / 10) - 2 * lastDigit;
}
return (n % 7 === 0) ? "Divisible by 7" : "Not divisible by 7";
}
var number = 8955795758;
console.log(isDivisibleBy7(number));
|
Time complexity: O(log10 n)
Auxiliary space: O(1)
Share your thoughts in the comments
Please Login to comment...