Check if N can be represented as sum of squares of two consecutive integers

Last Updated : 08 Apr, 2021

Given an integer N, the task is to check whether N can be represented as a sum of squares of two consecutive integers or not.

Examples:

Input: N = 5
Output: Yes
Explanation:
The integer 5 = 1² + 2² where 1 and 2 are consecutive numbers.
Input: 13
Output: Yes
Explanation:
13 = 2² + 3²

Approach: This equation can be represented as:

=> $N = K^{2} + (K - 1)^{2}$
=> $N = 2*K^{2} - 2*K + 1$
=> $K = \frac{2 + \sqrt{8*N - 4}}{2}$

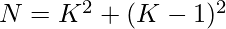
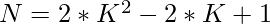
Finally, check the value of computed using this formula is an integer, which means that N can be represented as the sum of squares 2 consecutive integers

Below is the implementation of the above approach:

C++

// C++ implementation to check that
// a number is sum of squares of 2
// consecutive numbers or not
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to check that the
// a number is sum of squares of 2
// consecutive numbers or not
bool isSumSquare(int N)
{
    float n
        = (2 + sqrt(8 * N - 4))
          / 2;
 
    // Condition to check if the
    // a number is sum of squares of 2
    // consecutive numbers or not
    return (n - (int)n) == 0;
}
 
// Driver Code
int main()
{
    int i = 13;
 
    // Function call
    if (isSumSquare(i)) {
        cout << "Yes";
    }
    else {
        cout << "No";
    }
    return 0;
}

Java

// Java implementation to check that
// a number is sum of squares of 2
// consecutive numbers or not
import java.lang.Math;
 
class GFG{
     
// Function to check that the
// a number is sum of squares of 2
// consecutive numbers or not
public static boolean isSumSquare(int N)
{
    double n = (2 + Math.sqrt(8 * N - 4)) / 2;
     
    // Condition to check if the
    // a number is sum of squares of 2
    // consecutive numbers or not
    return(n - (int)n) == 0;
}
 
// Driver code
public static void main(String[] args)
{
    int i = 13;
 
    // Function call
    if (isSumSquare(i))
    {
        System.out.println("Yes");
    }
    else
    {
        System.out.println("No");
    }
}
}
 
// This code is contributed by divyeshrabadiya07

Python3

# Python3 implementation to check that
# a number is sum of squares of 2
# consecutive numbers or not
import math
 
# Function to check that the a
# number is sum of squares of 2
# consecutive numbers or not
def isSumSquare(N):
 
    n = (2 + math.sqrt(8 * N - 4)) / 2
     
    # Condition to check if the a
    # number is sum of squares of
    # 2 consecutive numbers or not
    return (n - int(n)) == 0
 
# Driver code
if __name__=='__main__':
     
    i = 13
     
    # Function call
    if isSumSquare(i):
        print('Yes')
    else :
        print('No')
 
# This code is contributed by rutvik_56

C#

// C# implementation to check that
// a number is sum of squares of 2
// consecutive numbers or not
using System;
class GFG{
     
// Function to check that the
// a number is sum of squares of 2
// consecutive numbers or not
public static bool isSumSquare(int N)
{
    double n = (2 + Math.Sqrt(8 * N - 4)) / 2;
     
    // Condition to check if the
    // a number is sum of squares of 2
    // consecutive numbers or not
    return(n - (int)n) == 0;
}
 
// Driver code
public static void Main(String[] args)
{
    int i = 13;
 
    // Function call
    if (isSumSquare(i))
    {
        Console.WriteLine("Yes");
    }
    else
    {
        Console.WriteLine("No");
    }
}
}
 
// This code is contributed by sapnasingh4991

Javascript

<script>
 
// Javascript implementation to check that
// a number is sum of squares of 2
// consecutive numbers or not
 
// Function to check that the
// a number is sum of squares of 2
// consecutive numbers or not
function isSumSquare(N)
{
    var n = (2 + Math.sqrt(8 * N - 4)) / 2;
 
    // Condition to check if the
    // a number is sum of squares of 2
    // consecutive numbers or not
    return (n - parseInt( n)) == 0;
}
 
// Driver code
var i = 13;
 
// Function call
if (isSumSquare(i))
{
    document.write("Yes");
}
else
{
    document.write("No");
}
 
// This code is contributed by todaysgaurav
 
</script>

Output:

Yes

Note: In order to print the integers, we can easily solve the above equation to get the roots.

Time Complexity: O(1)

Auxiliary Space: O(1)

Attention reader! Don’t stop learning now. Get hold of all the important mathematical concepts for competitive programming with the Essential Maths for CP Course at a student-friendly price. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

My Personal Notes

Related Articles

Check if N can be represented as sum of squares of two consecutive integers

C++

Java

Python3

C#

Javascript