Check if a graphs has a cycle of odd length
Last Updated :
20 Feb, 2023
Given a graph, the task is to find if it has a cycle of odd length or not.


The idea is based on an important fact that a graph does not contain a cycle of odd length if and only if it is Bipartite, i.e., it can be colored with two colors.
It is obvious that if a graph has an odd length cycle then it cannot be Bipartite. In Bipartite graph there are two sets of vertices such that no vertex in a set is connected with any other vertex of the same set). For a cycle of odd length, two vertices must of the same set be connected which contradicts Bipartite definition.
Let us understand converse, if a graph has no odd cycle then it must be Bipartite. Below is a induction based proof of this taken from http://infohost.nmt.edu/~math/faculty/barefoot/Math321Spring98/BipartiteGraphsAndEvenCycles.html
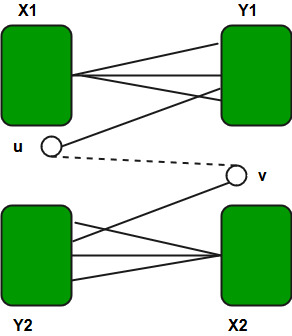
Assume that (X, Y) is a bipartition of G and let C = u1, u2, . . . , uk be a cycle of G, where u1 is in the vertex set X (abbreviated u1 ? X). If u1 ?X then u2 ? Y, . . . and, in general, u2j+1 ?X and u2i ?Y. Since C is a cycle, uk ?Y, so that k = 2s for some positive integer s. Therefore cycle C is even.
Assume that graph G has no odd cycles. It will be shown that such a graph is bipartite. The proof is induction on the number of edges. The assertion is clearly true for a graph with at most one edge. Assume that every graph with no odd cycles and at most q edges is bipartite and let G be a graph with q + 1 edges and with no odd cycles. Let e = uv be an edge of G and consider the graph H = G – uv. By induction, H has a bipartition (X, Y). If e has one end in X and the other end in Y then (X, Y) is a bipartition of G. Hence, assume that u and v are in X. If there were a path, P, between u and v in H then the length of P would be even. Thus, P + uv would be an odd cycle of G. Therefore, u and v must be in lie in different “pieces” or components of H. Thus, we have:

where X = X1 & X2 and Y = Y1 ? Y2. In this case it is clear that (X1 ? Y2, X2 ? Y1) is a bipartition of G.
Therefore we conclude that every graph with no odd cycles is bipartite. One can construct a bipartition as follows:
- Choose an arbitrary vertex x0 and set X0 = {x0}.
- Let Y0 be the set of all vertices adjacent to x0 and iterate steps 3-4.
- Let Xk be the set of vertices not chosen that are adjacent to a vertex of Yk-1.
- Let Yk be the set of vertices not chosen that are adjacent to a vertex of Xk-1.
- If all vertices of G have been chosen then
X = X0 ? X1 ? X2 ?. . . and Y = Y0 ? Y1 ? Y2 ? . . .
Below is code to check if a graph has odd cycle or not. The code basically checks whether graph is Bipartite.
C++
#include <bits/stdc++.h>
#define V 4
using namespace std;
bool containsOdd(int G[][V], int src)
{
int colorArr[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
colorArr[src] = 1;
queue <int> q;
q.push(src);
while (!q.empty())
{
int u = q.front();
q.pop();
if (G[u][u] == 1)
return true;
for (int v = 0; v < V; ++v)
{
if (G[u][v] && colorArr[v] == -1)
{
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
else if (G[u][v] && colorArr[v] == colorArr[u])
return true;
}
}
return false;
}
int main()
{
int G[][V] = {{0, 1, 0, 1},
{1, 0, 1, 0},
{0, 1, 0, 1},
{1, 0, 1, 0}
};
containsOdd(G, 0) ? cout << "Yes" : cout << "No";
return 0;
}
|
Java
import java.util.*;
class GFG {
public static int V =4;
public static boolean containsOdd(int G[][], int src)
{
int colorArr[] = new int[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
colorArr[src] = 1;
LinkedList<Integer> q = new LinkedList<Integer>();
q.add(src);
while (!q.isEmpty())
{
int u = q.peek();
q.pop();
if (G[u][u] == 1)
return true;
for (int v = 0; v < V; ++v)
{
if (G[u][v] == 1 && colorArr[v] == -1)
{
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
else if (G[u][v] == 1 && colorArr[v] ==
colorArr[u])
return true;
}
}
return false;
}
public static void main(String[] args)
{
int G[][] = {{0, 1, 0, 1},
{1, 0, 1, 0},
{0, 1, 0, 1},
{1, 0, 1, 0}};
if (containsOdd(G, 0))
System.out.println("Yes") ;
else
System.out.println("No");
}
}
|
Python3
import queue
def containsOdd(G, src):
global V
colorArr = [-1] * V
colorArr[src] = 1
q = queue.Queue()
q.put(src)
while (not q.empty()):
u = q.get()
if (G[u][u] == 1):
return True
for v in range(V):
if (G[u][v] and colorArr[v] == -1):
colorArr[v] = 1 - colorArr[u]
q.put(v)
elif (G[u][v] and
colorArr[v] == colorArr[u]):
return True
return False
V = 4
G = [[0, 1, 0, 1],
[1, 0, 1, 0],
[0, 1, 0, 1],
[1, 0, 1, 0]]
if containsOdd(G, 0):
print("Yes")
else:
print("No")
|
C#
using System;
using System.Collections.Generic;
class GFG
{
public static int V = 4;
public static bool containsOdd(int [,]G, int src)
{
int []colorArr = new int[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
colorArr[src] = 1;
Queue<int> q = new Queue<int>();
q.Enqueue(src);
while (q.Count != 0)
{
int u = q.Peek();
q.Dequeue();
if (G[u, u] == 1)
return true;
for (int v = 0; v < V; ++v)
{
if (G[u, v] == 1 && colorArr[v] == -1)
{
colorArr[v] = 1 - colorArr[u];
q.Enqueue(v);
}
else if (G[u,v] == 1 && colorArr[v] ==
colorArr[u])
return true;
}
}
return false;
}
public static void Main()
{
int [,]G = {{0, 1, 0, 1},
{1, 0, 1, 0},
{0, 1, 0, 1},
{1, 0, 1, 0}};
if (containsOdd(G, 0))
Console.WriteLine("Yes") ;
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
var V = 4;
function containsOdd(G, src)
{
var colorArr = Array(V).fill(-1);
colorArr[src] = 1;
var q = [];
q.push(src);
while (q.length != 0)
{
var u = q[0];
q.shift();
if (G[u][u] == 1)
return true;
for (var v = 0; v < V; ++v)
{
if (G[u][v] == 1 && colorArr[v] == -1)
{
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
else if (G[u][v] == 1 && colorArr[v] ==
colorArr[u])
return true;
}
}
return false;
}
var G = [[0, 1, 0, 1],
[1, 0, 1, 0],
[0, 1, 0, 1],
[1, 0, 1, 0]];
if (containsOdd(G, 0))
document.write("Yes") ;
else
document.write("No");
</script>
|
Time complexity: O(V^2),The time complexity of the algorithm is O(V^2) as the outer loop runs V times and the inner loop runs V times for every iteration of the outer loop.
Space complexity: O(V),The space complexity is O(V) as we use an array of size V to store the color of the vertices.
The above algorithm works only if the graph is strongly connected. We can extend it for the cases when graph is not strongly connected (Please refer this for details). In the above code, we always start with source 0 and assume that vertices are visited from it. One important observation is a graph with no edges is also Bipartite. Note that the Bipartite condition says all edges should be from one set to another.
Share your thoughts in the comments
Please Login to comment...