Calculate area and height of an isosceles triangle whose sides are radii of a circle
Last Updated :
14 Apr, 2021
Given integers R and 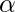 representing the radius of a circle and the angle formed at the center O by the sector AB (as shown in the figure below), the task is to find the height and area of the triangle formed by connecting the points A, B, and O if possible. Otherwise, print “Not possible”.
representing the radius of a circle and the angle formed at the center O by the sector AB (as shown in the figure below), the task is to find the height and area of the triangle formed by connecting the points A, B, and O if possible. Otherwise, print “Not possible”.

Examples:
Input: R = 5, 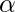 = 120
= 120
Output:
Height of the triangle is 2.5
Area of triangle is 10.8253
Explanation: The given area and height can be calculated using the equations:
Height = 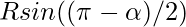
Area = 
Input: R = 12, 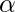 = 240
= 240
Output: Not possible
Approach: The given problem can be solved based on the following observations:
Observations:

- Suppose a perpendicular is drawn on chord AB from point O and the perpendicular cuts the chord at point D. Then the height of the triangle will be OD.>
- According to property of circle the point D divides the chord AB in two equal parts and triangle AOD and BOD will be similar triangle.>
- The angles ?OAB and ?OBA are also equal as triangle AOD and BOD are similar and is equal to
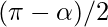
- The height of the triangle OAB can be calculated using the formula:
- The area of the triangle can be calculated as:
Follow the steps below to solve the problem:>
- Check if the angle is greater than 180 or is equal to 0 then print “Not possible”.
- Now convert the angle in radian.
- Calculate the angle ?OAB and ?OBA as
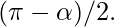
- Now print the height and area of triangle OAB after calculating it using the above-discussed formula.
Below is the implementation of the above approach:>
C++
#include <bits/stdc++.h>
using namespace std;
double Convert(double degree)
{
double pi = 3.14159265359;
return (degree * (pi / 180));
}
void areaAndHeightOfTraingle(
double radius,
double a)
{
if (a >= 180 || a == 0) {
cout << "Not possible";
return;
}
double base_angle = (180 - a) / 2;
double radians = Convert(base_angle);
double height = sin(radians) * radius;
cout << "Height of triangle "
<< height << endl;
double base = cos(radians) * radius;
double area = base * height;
cout << "Area of triangle "
<< area << endl;
}
int main()
{
double R = 5, angle = 120;
areaAndHeightOfTraingle(R, angle);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static double Convert(double degree)
{
double pi = 3.14159265359;
return (degree * (pi / 180));
}
static void areaAndHeightOfTraingle(
double radius, double a)
{
if (a >= 180 || a == 0)
{
System.out.println("Not possible");
return;
}
double base_angle = (180 - a) / 2;
double radians = Convert(base_angle);
double height = Math.sin(radians) * radius;
System.out.println("Height of triangle " + height);
double Base = Math.cos(radians) * radius;
double area = Base * height;
System.out.println("Area of triangle " + area);
}
public static void main(String[] args)
{
double R = 5, angle = 120;
areaAndHeightOfTraingle(R, angle);
}
}
|
Python3
from math import sin,cos
def Convert(degree):
pi = 3.14159265359
return (degree * (pi / 180))
def areaAndHeightOfTraingle(radius, a):
if (a >= 180 or a == 0):
print("Not possible")
return
base_angle = (180 - a) / 2
radians = Convert(base_angle)
height = sin(radians) * radius
print("Height of triangle ", round(height, 1))
base = cos(radians) * radius
area = base * height
print("Area of triangle ", round(area, 4))
if __name__ == '__main__':
R , angle = 5, 120
areaAndHeightOfTraingle(R, angle)
|
C#
using System;
public class GFG
{
static double Convert(double degree)
{
double pi = 3.14159265359;
return (degree * (pi / 180));
}
static void areaAndHeightOfTraingle(
double radius, double a)
{
if (a >= 180 || a == 0)
{
Console.WriteLine("Not possible");
return;
}
double base_angle = (180 - a) / 2;
double radians = Convert(base_angle);
double height = Math.Sin(radians) * radius;
Console.WriteLine("Height of triangle " + height);
double Base = Math.Cos(radians) * radius;
double area = Base * height;
Console.WriteLine("Area of triangle " + area);
}
static public void Main ()
{
double R = 5, angle = 120;
areaAndHeightOfTraingle(R, angle);
}
}
|
Javascript
<script>
function Convert(degree)
{
var pi = 3.14159265359;
return (degree * (pi / 180));
}
function areaAndHeightOfTraingle(radius, a)
{
if (a >= 180 || a == 0)
{
document.write("Not possible");
return;
}
var base_angle = (180 - a) / 2;
var radians = Convert(base_angle);
var height = Math.sin(radians) * radius;
document.write("Height of triangle " + height + "<br>");
var Base = Math.cos(radians) * radius;
var area = Base * height;
document.write("Area of triangle " + area);
}
var R = 5, angle = 120;
areaAndHeightOfTraingle(R, angle);
</script>
|
Output: Height of triangle 2.5
Area of triangle 10.8253
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...