Program to find area of a triangle
Last Updated :
16 Feb, 2023
Given the sides of a triangle, the task is to find the area of this triangle.
Examples :
Input : a = 5, b = 7, c = 8
Output : Area of a triangle is 17.320508
Input : a = 3, b = 4, c = 5
Output : Area of a triangle is 6.000000
Approach: The area of a triangle can simply be evaluated using following formula.
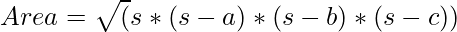
where a, b and c are lengths of sides of triangle, and
s = (a+b+c)/2

Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float findArea(float a, float b, float c)
{
if (a < 0 || b < 0 || c < 0 ||
(a + b <= c) || a + c <= b ||
b + c <= a)
{
cout << "Not a valid triangle";
exit(0);
}
float s = (a + b + c) / 2;
return sqrt(s * (s - a) *
(s - b) * (s - c));
}
int main()
{
float a = 3.0;
float b = 4.0;
float c = 5.0;
cout << "Area is " << findArea(a, b, c);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
float findArea(float a, float b, float c)
{
if (a < 0 || b < 0 || c <0 || (a+b <= c) ||
a+c <=b || b+c <=a)
{
printf("Not a valid triangle");
exit(0);
}
float s = (a+b+c)/2;
return sqrt(s*(s-a)*(s-b)*(s-c));
}
int main()
{
float a = 3.0;
float b = 4.0;
float c = 5.0;
printf("Area is %f", findArea(a, b, c));
return 0;
}
|
Java
class Test
{
static float findArea(float a, float b, float c)
{
if (a < 0 || b < 0 || c <0 || (a+b <= c) ||
a+c <=b || b+c <=a)
{
System.out.println("Not a valid triangle");
System.exit(0);
}
float s = (a+b+c)/2;
return (float)Math.sqrt(s*(s-a)*(s-b)*(s-c));
}
public static void main(String[] args)
{
float a = 3.0f;
float b = 4.0f;
float c = 5.0f;
System.out.println("Area is " + findArea(a, b, c));
}
}
|
Python3
def findArea(a,b,c):
if (a < 0 or b < 0 or c < 0 or (a+b <= c) or (a+c <=b) or (b+c <=a) ):
print('Not a valid triangle')
return
s = (a + b + c) / 2
area = (s * (s - a) * (s - b) * (s - c)) ** 0.5
print('Area of a triangle is %f' %area)
a = 3.0
b = 4.0
c = 5.0
findArea(a,b,c)
|
C#
using System;
class Test {
static float findArea(float a, float b,
float c)
{
if (a < 0 || b < 0 || c <0 ||
(a + b <= c) || a + c <=b ||
b + c <=a)
{
Console.Write("Not a valid triangle");
System.Environment.Exit(0);
}
float s = (a + b + c) / 2;
return (float)Math.Sqrt(s * (s - a) *
(s - b) * (s - c));
}
public static void Main()
{
float a = 3.0f;
float b = 4.0f;
float c = 5.0f;
Console.Write("Area is " + findArea(a, b, c));
}
}
|
PHP
<?php
function findArea($a, $b, $c)
{
if ($a < 0 or $b < 0 or
$c < 0 or ($a + $b <= $c) or
$a + $c <= $b or $b + $c <= $a)
{
echo "Not a valid triangle";
exit(0);
}
$s = ($a + $b + $c) / 2;
return sqrt($s * ($s - $a) *
($s - $b) * ($s - $c));
}
$a = 3.0;
$b = 4.0;
$c = 5.0;
echo "Area is ", findArea($a, $b, $c);
?>
|
Javascript
<script>
function findArea( a, b, c)
{
if (a < 0 || b < 0 || c < 0 ||
(a + b <= c) || a + c <= b ||
b + c <= a)
{
document.write( "Not a valid triangle");
return;
}
let s = (a + b + c) / 2;
return Math.sqrt(s * (s - a) *
(s - b) * (s - c));
}
let a = 3.0;
let b = 4.0;
let c = 5.0;
document.write( "Area is " + findArea(a, b, c));
</script>
|
Time Complexity: O(log2n)
Auxiliary Space: O(1), since no extra space has been taken.
Given the coordinates of the vertices of a triangle, the task is to find the area of this triangle.
Approach: If given coordinates of three corners, we can apply the Shoelace formula for the area below.
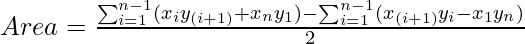
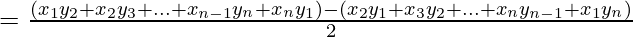
C++
#include <bits/stdc++.h>
using namespace std;
double polygonArea(double X[], double Y[], int n)
{
double area = 0.0;
int j = n - 1;
for (int i = 0; i < n; i++)
{
area += (X[j] + X[i]) * (Y[j] - Y[i]);
j = i;
}
return abs(area / 2.0);
}
int main()
{
double X[] = {0, 2, 4};
double Y[] = {1, 3, 7};
int n = sizeof(X)/sizeof(X[0]);
cout << polygonArea(X, Y, n);
}
|
Java
import java.io.*;
import java.math.*;
class GFG {
static double polygonArea(double X[], double Y[], int n)
{
double area = 0.0;
int j = n - 1;
for (int i = 0; i < n; i++)
{
area += (X[j] + X[i]) * (Y[j] - Y[i]);
j = i;
}
return Math.abs(area / 2.0);
}
public static void main (String[] args)
{
double X[] = {0, 2, 4};
double Y[] = {1, 3, 7};
int n = X.length;
System.out.println(polygonArea(X, Y, n));
}
}
|
Python3
def polygonArea(X,Y, n) :
area = 0.0
j = n - 1
for i in range( 0, n) :
area = area + (X[j] + X[i]) * (Y[j] - Y[i])
j = i
return abs(area // 2.0)
X = [0, 2, 4]
Y = [1, 3, 7]
n = len(X)
print(polygonArea(X, Y, n))
|
C#
using System;
class GFG {
static double polygonArea(double []X,
double []Y, int n)
{
double area = 0.0;
int j = n - 1;
for (int i = 0; i < n; i++)
{
area += (X[j] + X[i]) *
(Y[j] - Y[i]);
j = i;
}
return Math.Abs(area / 2.0);
}
public static void Main ()
{
double []X = {0, 2, 4};
double []Y = {1, 3, 7};
int n = X.Length;
Console.WriteLine(
polygonArea(X, Y, n));
}
}
|
PHP
<?php
function polygonArea( $X, $Y, $n)
{
$area = 0.0;
$j = $n - 1;
for ( $i = 0; $i < $n; $i++)
{
$area += ($X[$j] + $X[$i]) *
($Y[$j] - $Y[$i]);
$j = $i;
}
return abs($area / 2.0);
}
$X = array(0, 2, 4);
$Y = array(1, 3, 7);
$n = count($X);
echo polygonArea($X, $Y, $n);
?>
|
Javascript
<script>
function polygonArea(X, Y, n)
{
let area = 0.0;
let j = n - 1;
for (let i = 0; i < n; i++)
{
area += (X[j] + X[i]) * (Y[j] - Y[i]);
j = i;
}
return Math.abs(area / 2.0);
}
let X = [0, 2, 4];
let Y = [1, 3, 7];
let n = X.length;
document.write(polygonArea(X, Y, n));
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...