Axiomatic Probability in R

Axiomatic probability, also known as the measure-theoretic or Kolmogorov’s probability, is a foundational approach to probability theory that establishes a rigorous mathematical framework for understanding random events and uncertainty. It was developed by the Russian mathematician Andrey Kolmogorov in the 1930s and has become the standard framework for modern probability theory.

Key Concepts in Axiomatic Probability:

Sample Space (Ω): Axiomatic probability begins with the concept of a sample space, denoted by Ω. The sample space represents the set of all possible outcomes of a random experiment.

For example, if you’re rolling a six-sided die, Ω would be {1, 2, 3, 4, 5, 6}.

Event: An event is a subset of the sample space Ω. It represents a specific outcome or a collection of outcomes of the random experiment. Events are denoted by capital letters, such as A, B, or C.

Tossing two dice: We have

S = {1,2,3,4,5,6}²

Event: We define

E =(Sum of dice is equal to 7)

Mathematical Explanation :

The axioms of Kolmogorov.

Let S denote an event set with a probability measure P defined over it, such that probability of any event A ⊂ S is given by P(A). Then, the probability measure obeys the following axioms:

1. Non Negative Axiom: P(A) ≥ 0 ∀ A
2. Normalisation: P(S) = 1,
3. Finite Additivity: If {A1,A2,…Aj,…} is a sequence of mutually exclusive events such that Ai ∩ Aj = ∅ for all i, j, then P(A1 ∪ A2 ∪···∪Aj ∪···) = P(A1)+P(A2)+···+P(Aj)+···.

The axioms are supplemented by two definitions:

1. The conditional probability of A given B is defined by

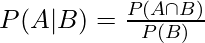
2. The events A, B are said to be statistically independent if

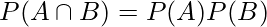
In the R programming language, axiomatic probability itself is not a particular idea or function. The preceding response explained axiomatic probability mathematically. It gives a collection of axioms—basic ideas—upon which probability theory may be constructed. Non-negativity, normalisation, and additivity are among these axioms, which was previously mentioned.

Working with probability distributions and performing probabilistic computations in R need the application of axiomatic probability concepts. Numerous functions and packages are available in R for probability and statistics, including distributions for specifying probability distributions, p functions for computing cumulative probabilities, and q functions for quantiles, among others.

Demonstrating Axiomatic Probability Axioms with a Six-Sided Fair Die

Axiomatic probability, grounded in mathematical principles, is the foundation of probability theory. We’ll demonstrate this concept in R using a simple example involving a six-sided fair die. The three axioms of probability—non-negativity, normalization, and additivity—are key to understanding this.

R

# Sample space S for a six-sided fair die
sample_space <- 1:6

# Probability of each outcome
prob_each_outcome <- rep(1/6, 6)

# Non-Negativity Axiom (already satisfied)

# Normalization Axiom
sum_of_probabilities <- sum(prob_each_outcome)
cat("Sum of probabilities in the sample space S:", sum_of_probabilities, "\n")

# Additivity Axiom
# Let's consider two events: rolling an even number and rolling an odd number
event_even <- c(2, 4, 6)
event_odd <- c(1, 3, 5)

# Probability of the union of two events
probability_union <- sum(prob_each_outcome[event_even]) +
    sum(prob_each_outcome[event_odd])
cat("Probability of rolling an even or an odd number:", probability_union, "\n")

Output :

Sum of probabilities in the sample space S: 1 
Probability of rolling an even or an odd number: 1 

In this code, we define a sample space for a fair six-sided die and assign equal probabilities to each outcome, satisfying the non-negativity and normalization axioms. Then, we calculate the probability of rolling an even or an odd number, demonstrating the additivity axiom. The output shows that the sum of probabilities equals 1, as per the normalization axiom, and the probability of the union of the two events equals 1, consistent with the additivity axiom.

The line “Sum of probabilities in the sample space S: 1” demonstrates that the probabilities assigned to each outcome in the sample space (a fair six-sided die) sum up to 1, satisfying the normalization axiom.

The line “Probability of rolling an even or an odd number: 1” shows that when we calculate the probability of rolling either an even or an odd number (two mutually exclusive events), the result is 1, fulfilling the additivity axiom.

Examples of Axiomatic Probability in R :

Probability of Tossing a Fair Coin

Let’s calculate the probability of getting heads (H) when tossing a fair coin.

R

# Define the sample space
sample_space_coin <- c("H", "T")

# Define the event of getting heads
event_H <- "H"

# Calculate the probability of getting heads
P_H <- length(event_H) / length(sample_space_coin)

cat("Probability of getting heads:", P_H, "\n")

Output :

Probability of getting heads: 0.5 

In this code, we have a sample space representing the outcomes of a coin toss (H for heads and T for tails). We calculate the probability of getting heads (event_H) by dividing the number of favourable outcomes by the total number of outcomes.

Probability of Drawing Cards

Suppose you have a standard deck of 52 playing cards. Calculate the probability of drawing a red card (hearts or diamonds).

R

# Define the sample space for a deck of cards
suits <- c("Hearts", "Diamonds", "Clubs", "Spades")
ranks <- c(2:10, "Jack", "Queen", "King", "Ace")
sample_space_cards <- expand.grid(Suit = suits, Rank = ranks)

# Define the event of drawing a red card
red_suits <- c("Hearts", "Diamonds")
event_red_card <- sample_space_cards[sample_space_cards$Suit %in% red_suits, ]

# Calculate the probability of drawing a red card
P_red_card <- nrow(event_red_card) / nrow(sample_space_cards)

cat("Probability of drawing a red card:", P_red_card, "\n")

Output:

Probability of drawing a red card: 0.5 

Here, we define the sample space to represent a standard deck of cards. The event of drawing a red card consists of cards with suits Hearts and Diamonds. We calculate the probability of drawing a red card by dividing the number of red cards by the total number of cards in the deck.

Probability of Rolling a Prime Number on a Fair Six-Sided Die

In this example, we’ll calculate the probability of rolling a prime number (2, 3, or 5) on a fair six-sided die.

R

# Define the sample space for rolling a fair six-sided die
sample_space_die <- 1:6

# Define the event of rolling a prime number
event_prime <- c(2, 3, 5)

# Calculate the probability of rolling a prime number
P_prime <- length(event_prime) / length(sample_space_die)

cat("Probability of rolling a prime number:", P_prime, "\n")

Output:

Probability of rolling a prime number: 0.5 

This code defines the sample space for rolling a fair six-sided die, identifies the event of rolling a prime number, and calculates the probability of rolling a prime number on the die. It should run successfully in most online R compilers, and the expected output will be the probability of rolling a prime number.

Conclusion

Axiomatic probability, introduced by Kolmogorov, underpins modern probability theory. This article explains key concepts and demonstrates their use in R. It covers defining distributions, calculating probabilities, and offers practical examples, empowering data analysis across domains.