Probability Theorems | Theorems and Examples

Last Updated : 29 Sep, 2023

What is Probability?

Probability can be defined as the possibility of occurrence of an event. Probability is the likelihood or the chances that an uncertain event will occur. The probability of an event always lies between 0 and 1.

$Probability(P)=\frac{Favourable~Outcomes}{Total~Outcomes}$

$P(A)=\frac{n(A)}{n(S)}$

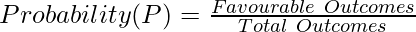
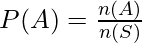
Where,

P(A) represents the probability of event A,

n(A) represents the number of favourable outcomes, and

n(S) represents total outcomes in sample space.

Terminologies associated with probability
1. Event: Each outcome of an experiment or trial that is conducted is termed an event.

2. Sample Space: The set of all the possible outcomes of an experiment is called the sample space of that experiment and is generally represented as S.

3. Sure Event: An event that will always occur is called a sure event. A sure event has a probability of 1.

4. Impossible Event: An event that will never occur is called an impossible event. An impossible event has a probability of 0.

5. Favorable Outcome: An event that produces the desired result in an experiment is called a favourable outcome for that experiment.

6. Independent Events: Two events are said to be independent if the occurrence of one event does not depend upon the other.

7. Mutually Exclusive Events: Two events are said to be mutually exclusive if they cannot occur together or simultaneously.

8. Overlapping Events: The events that can happen individually as well as jointly are said to be overlapping events.

Probability Theorems

I. Theorem of Complementary Events

Two events are said to be complementary events if the sum of their probability is 1. Thus, if A is an event and the probability of A is given by P(A) then this theorem states that

P(A’) = 1 – P(A)

where P(A’) is the probability of the complementary event of A; i.e., A’. In such cases, events A and A’ are said to be mutually exhaustive also.

Example:

Consider an event A that 3 will appear on rolling a dice. Calculate the probability of not getting a 3.

Solution:

Probability of getting a 3 on dice = 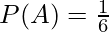$P(A)=\frac{1}{6}$

The probability of A’ which is the probability of not getting a 3 is calculated using the theorem of complementary events as follows:

P(A’) = 1 – P(A)

$P(A')=1-\frac{1}{6}$

$P(A')=\frac{5}{6}$

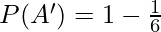
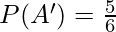
II. Theorem of Addition

Theorem of Addition is used when one has to determine the probability of occurrence of two or more events. In simple terms, this theorem is used to calculate the probability of union of two or more than two events. For instance, there are two events E₁ and E₂ of a given sample space. By using the theorem of addition, we can determine the probability that either E₁ or E₂ will occur. However, to determine the probability, first of all, we have to find out whether the events are mutually exclusive or overlapping, after that only the required probability is calculated using the correct rule or formula.

Theorem of Addition has two cases:

1. When the events are Mutually Exclusive

If A and B are mutually exclusive events then according to this theorem:

P(E₁⋃ E₂) = P(E₁) + P(E₂)

where, (E₁ ⋃ E₂) means either E₁ or E₂

If there are more than two events, then

P(E₁ ⋃ E₂ ⋃ …….. E_n) = P(E₁) + P(E₂) + ……… + P(E_n)

If these events are collectively exhaustive, then

P(E₁ ⋃ E₂ ⋃ …….. E_n) = P(E₁) + P(E₂) + ……… + P(E_n) = 1

This rule is known as the Theorem of Addition for Mutually Exclusive Events.

Example:

If A and B are events of occurrence of 2 and occurrence of 3 on a dice respectively, then calculate the probability of occurrence of A or B; i.e., getting 2 or 3 on dice.

Solution:

$Probability~of~getting~2=P(A)=\frac{1}{6}$

$Probability~of~getting~3=P(B)=\frac{1}{6}$

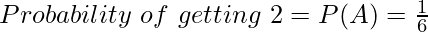
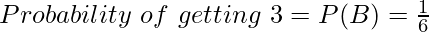
As A and B are independent and mutually exclusive events, using the theorem of addition,

P(A⋃B) = P(A) + P(B)

P(A⋃B)=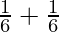 $\frac{1}{6}+\frac{1}{6}$

P(A⋃B)=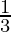 $\frac{1}{3}$

2. When the Events are Overlapping

When the events are overlapping, the theorem of addition determines the probability that one or more events would occur in a single trial.

If E₁ and E₂ are overlapping events then according to this theorem:

P(E₁ ⋃ E₂) = P(E₁) + P(E₂) – P(E₁⋂ E₂)

where, P(E₁ ⋃ E₂) is the probability that either E₁ or E₂ or both events will occur, and P(E₁ ⋂ E₂) is the joint probability that indicates the probability of occurrence of both E₁ and E₂.

If there are three events E₁, E₂, and E₃, then

P(E₁ ⋃ E₂ ⋃ E₃) = P(E₁) + P(E₂) + P(E₃) – P(E₁ ⋂ E₂) – P(E₁ ⋂ E₃) – P(E₂ ⋂ E₃) + P(E₁ ⋂ E₂ ⋂ E₃)

where P(E₁ ⋃ E₂ ⋃ E₃) gives the probability of occurrence of at least one of the events; E₁, E₂, and E₃.

Example:

Consider a class with 20 students. 10 students passed in Maths, 15 in English, and 13 in both. What is the probability that a student passed in either Math or English?

Solution:

Total students = 20

P(A) = Probability that a student passed in Maths = 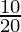$\frac{10}{20}$

P(B) = Probability that a student passed in English = 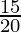$\frac{15}{20}$

P(A⋂B) = Probability that a student passed in both Math and English = 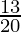$\frac{13}{20}$

This is a case of overlapping events as some students who passed in Math may have passed in English too and some students who passed in English may have passed in Math too. Thus we need to remove these common students from the sum of students who passed in Math and English. Thus, using the theorem of addition for overlapping events, we get:

The probability that a student passed either in Maths or in English = P(A⋃B)

P(A⋃B) = P(A) + P(B) – P(A⋂B)

P(A⋃B) = 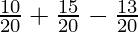$\frac{10}{20}+\frac{15}{20}-\frac{13}{20}$

P(A⋃B) = 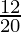$\frac{12}{20}$

P(A⋃B) = 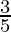$\frac{3}{5}$

III. Theorem of Multiplication

When we have to determine the probability of joint occurrence or occurrence in unison of two or more than two events, the theorem of multiplication is used. For instance, the probability of getting the same number on two dice tossed simultaneously, drawing different coloured balls from a box having red, blue, and green balls.

There are 2 cases in theorem of multiplication:

1. When events are Independent

If E₁ and E₂ are independent events with P(E₁) ≠ 0 and P(E₂) ≠ 0, then according to this theorem of probability:

P(E₁⋂ E₂) = P(E₁).P(E₂) $\text{[math]}$

This means that the probability of intersection of two events E₁ and E₂ is equal to the product of the individual probabilities of events E₁ and E₂.

If there are more than two events; say, E₁, E₂, and E₃, then,

P(E₁ ⋂ E₂ ⋂ E₃) = P(E₁).P(E₂).P(E₃)

Example:

A statistics problem is given to two students, say A and B. Their chances of solving it correctly are known to be 0.5 and 0.3, respectively. Find the probability that both of them solve it.

Solution:

Let E₁ be the event of A solving the problem and E₂ is the event of B solving the problem. Here event E₁ and E₂ are independent.

$P(E_1)=0.5$

$P(E_2)=0.3$

$P(E_1⋂E_2)=P(E_1)×P(E_2)$

$P(E_1⋂E_2)=0.5\times0.3$

$P(E_1⋂E_2)=0.15$

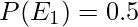
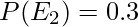
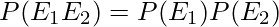
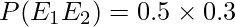
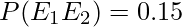
Therefore, the chances of both A and B solving the problem is 15%.

2. When Events are not Independent

If the events are not independent, then multiplication theorem states that the joint probability of the events E₁ and E₂ is given by the probability of event E₁ multiplied by the probability of event E₂ given that event E₁ has occurred and vice-versa. Simply put, the rule uses the concept of conditional probability when the events are known to be dependent or non-independent. According to this theorem, if E₁ and E₂ are two events where P(E₁) ≠ 0 and P(E₂) ≠ 0, and if E₁ and E₂ are not independent events, then:

P(E₁⋂ E₂) = P(E₁).P(E₂/E₁)

P(E₁ ⋂ E₂) = P(E₂).P(E₁/E₂)

Similarly, if there are three dependent events E₁, E₂, and E₃, then,

P(E₁ ⋂ E₂ ⋂ E₃) = P(E₁).P(E₂/E₁).P(E₃/E₁⋂E₂)

Example:

A large company employs 70 engineers, of whom 36 are males and the remaining are females. Of the female engineers. 14 are under 35 years of age, 15 are between 35 and 45 years of age, and the remaining are over 45 years of age. What is the probability of randomly selected engineer who is a female and under the age of 35 years of age?

Solution:

Let E₁ represent the event that an engineer selected at random is a female and E₂ is the event that a female engineer selected is under 35 years of age.

Since there are 36 males out of 70 engineers, it means that the number of female engineers is 34.

P(E₁) = 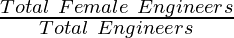$\frac{Total~Female~Engineers}{Total~Engineers}$

P(E₁) = 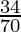$\frac{34}{70}$

$P(\frac{E_2}{E_1})=\frac{14}{34}$

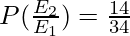
Therefore, P(E₁⋂E₂) = 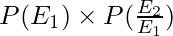$P(E_1)\times P(\frac{E_2}{E_1})$

P(E1⋂E2) = $\frac{34}{70}\times\frac{14}{34}$

P(E1⋂E2) = $\frac{1}{5}$

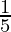
IV. Statistical Independence

If joint probability of two events E₁ and E₂ is equal to the product of marginal probability of E₁ and E₂, then E₁ and E₂ are said to be statistically independent. Mathematically, two events E₁ and E₂ are statistically independent if:

P(E₁⋂E₂) = P(E₁).P(E₂)

If this relationship does not hold true, events E₁ and E₂ are statistically not independent.

Example:

A number is selected randomly from the first n natural numbers. Let E₁ be the event that it is divisible by 2, and E₂ be the event that it is divisible by 3. Show that the events are statistically independent if n=96.

Solution:

When n=96,

$P(E_1)=\frac{48}{96}=\frac{1}{2}$

$P(E_2)=\frac{32}{96}=\frac{1}{3}$

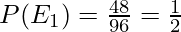
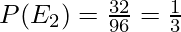
and 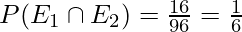$P(E_1\cap E_2)=\frac{16}{96}=\frac{1}{6}$

Here, 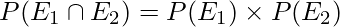$P(E_1\cap E_2)=P(E_1)\times P(E_2)$

as 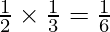$\frac{1}{2}\times\frac{1}{3}=\frac{1}{6}$

Hence, events E₁ and E₂ are statistically independent.

V. Theorem of Total Probability

The theorem of total probability, also known as Theorem of Elimination, is employed to calculate the probability of an event whose occurrence is dependent on the occurrence (or non-occurrence) of some intermediate events in the experimental process. If an event E is associated with other intermediate, mutually exclusive events H₁, H₂, …., H_n, then the total probability of its occurrence will be,

P(E) = P(H₁⋂ E) + P(H₂⋂ E) + …. + P(H_n⋂ E)

P(E) = P(H₁) x P(E/H₁) + P(H₂) x P(E/H₂) + ……… + P(H_n) x P(E/H_n)

Example:

Suppose that the accounting manager of a company wants to introduce a new policy of assessment of employees of the company for their promotion and the policy is subject to clearance from the general manager (GM). At present, the post of GM is vacant and is likely to be filled soon by appointing one of the three deputy GMs. The chances of policy in question being implemented are dependent on who is appointed the GM. Now, the chances of managers A, B, and C being appointed GM are 0.4, 0.5, and 0.1 respectively. While the likelihood of policy implementation is 0.2, 0.6, and 0.4, respectively, with the three. What is the probability that the policy will eventually be implemented?

Solution:

Let’s say H₁, H₂, and H₃ represent the respective events that A, B, and C are promoted, and E be the event that policy is implemented. Now,

P(H₁) = 0.4

P(H₂) = 0.5

P(H₃) = 0.1

P(E/H₁) = 0.2

P(E/H₂) = 0.6

P(E/H₃) = 0.4

Now, P(E) = P(H₁⋂E) + P(H₂⋂E) + P(H₃⋂E)

P(E) = P(H₁).P(E/H₁) + P(H₂).P(E/H₂) + P(H₃).P(E/H₃)

P(E) = (0.4)(0.2) + (0.5)(0.6) + (0.1)(0.4)

P(E) = 0.08 + 0.3 + 0.04

P(E) = 0.42

Therefore, the overall chances that the policy will be introduced are 42%.

Suggest improvement

Probability Theory

Share your thoughts in the comments

Probability Theorems | Theorems and Examples

What is Probability?

Terminologies associated with probability

Table of Content

Probability Theorems

I. Theorem of Complementary Events

Example:

Solution:

II. Theorem of Addition

1. When the events are Mutually Exclusive

Example:

Solution:

2. When the Events are Overlapping

Example:

Solution:

III. Theorem of Multiplication

1. When events are Independent

Example:

Solution:

2. When Events are not Independent

Example:

Solution:

IV. Statistical Independence

Example:

Solution:

V. Theorem of Total Probability

Example:

Solution:

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?