Auto-associative Neural Networks

Auto associative Neural networks are the types of neural networks whose input and output vectors are identical. These are special kinds of neural networks that are used to simulate and explore the associative process. Association in this architecture comes from the instruction of a set of simple processing elements called units which are connected through weighted connections.

In these networks, we performed training to store the vector either bipolar or binary. A stored vector can be retrieved from a distorted or noisy vector if the input is similar to it.

Architecture 

AANN contains five-layer perceptron feed-forward network, that can be divided into two neural networks of 3 layers each connected in series (similar to autoencoder architecture). The network consists of an input layer followed by a hidden layer and bottleneck layer. This bottleneck layer is common between both the network and a key component of the network. It provides data compression to the input and topology with powerful feature extraction capabilities. The bottleneck layer is followed by a second non-linear hidden layer and the output layer of the second network.

Auto-Associative NN architecture

The first network compresses the information of the n-dimensional vector to smaller dimension vectors that contain a smaller number of characteristic variables and represent the whole process. The second network works opposite to the first and uses compressed information to regenerate the original n redundant measures. 

Algorithm

We will be using Hebb Rule in the algorithm for setting weights because input and output vectors are perfectly correlated since the input and output both have the same number of output units and input units.

Hebb Rule:

• when A and B are positively correlated, then increase the strength of the connection between them.
• when A and B are negatively correlated, then decrease the strength of the connection between them.
• In practice, we use following formula to set the weights:

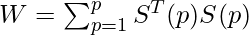
• where, W = weighted matrix
• T= Learning Rate
• S(p) : p-distinct n-dimensional prototype patterns

Training Algorithm

1. Initialize all weights for i= 1,2,3 …n and j= 1,2,3 …n such that: w_ij=0.
2. For each vector to be stored repeat the following steps:
3. Set activation for each input unit i= 1 to n: x_i = s_i.
4. Set activation for each output unit j= 1 to n: y_j = s_j.
5. Update the weights for i= 1,2,3 …n and j= 1,2,3 …n such that : w_ij (new) = w_ij (old) + x_iy_j

Testing / Inference Algorithm:

For testing whether the input is ‘known’ and ‘unknown’ to the model, we need to perform the following steps:

1. Take the weights that were generated during the training phase using Hebb’s rule.
2. For each input vector perform the following steps:
3. Set activation in the input units equal to input vectors.
4. Set activation in output units for j= 1,2,3 …n: 
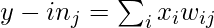
5. Apply activation function for j= 1, 2, 3 … n:

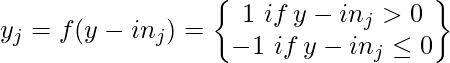
AANN recognizes the input vector to be known if the output unit after activation generated same pattern as one stored in it.

Storage Capacity

• One of the important features of AANN is the number of patterns that can be stored before the network begins to forget.
• The number of vectors that can be stored in the network is called the capacity of the network.
• The capacity of the vectors depends upon the relationship between them i.e more vectors can be stored if they are mutually orthogonal. Generally, n-1 mutually orthogonal vectors with n components can be stored.

Applications

Auto-associative Neural Networks can be used in many fields:

• Pattern Recognition
• Bio-informatics
• Voice Recognition
• Signal Validation etc.

References:

• RIT Presentation on Auto-Associative