Program for array left rotation by d positions.

Given an array of integers arr[] of size N and an integer, the task is to rotate the array elements to the left by d positions.

Examples:

Input: 
arr[] = {1, 2, 3, 4, 5, 6, 7}, d = 2
Output: 3 4 5 6 7 1 2

Input: arr[] = {3, 4, 5, 6, 7, 1, 2}, d=2
Output: 5 6 7 1 2 3 4

Approach 1 (Using temp array): This problem can be solved using the below idea:

After rotating d positions to the left, the first d elements become the last d elements of the array

• First store the elements from index d to N-1 into the temp array.
• Then store the first d elements of the original array into the temp array.
• Copy back the elements of the temp array into the original array

Illustration:

Suppose the give array is arr[] = [1, 2, 3, 4, 5, 6, 7], d = 2.

First Step:
    => Store the elements from 2nd index to the last.
    => temp[] = [3, 4, 5, 6, 7]

Second Step:
    => Now store the first 2 elements into the temp[] array.
    => temp[] = [3, 4, 5, 6, 7, 1, 2]

Third Steps:
    => Copy the elements of the temp[] array into the original array.
    => arr[] = temp[] So arr[] = [3, 4, 5, 6, 7, 1, 2]

Follow the steps below to solve the given problem. 

• Initialize a temporary array(temp[n]) of length same as the original array
• Initialize an integer(k) to keep a track of the current index
• Store the elements from the position d to n-1 in the temporary array
• Now, store 0 to d-1 elements of the original array in the temporary array
• Lastly, copy back the temporary array to the original array

Below is the implementation of the above approach : 

C++

#include <bits/stdc++.h>
using namespace std;

// Function to rotate array
void Rotate(int arr[], int d, int n)
{
    // Storing rotated version of array
    int temp[n];

    // Keeping track of the current index
    // of temp[]
    int k = 0;

    // Storing the n - d elements of
    // array arr[] to the front of temp[]
    for (int i = d; i < n; i++) {
        temp[k] = arr[i];
        k++;
    }

    // Storing the first d elements of array arr[]
    //  into temp
    for (int i = 0; i < d; i++) {
        temp[k] = arr[i];
        k++;
    }

    // Copying the elements of temp[] in arr[]
    // to get the final rotated array
    for (int i = 0; i < n; i++) {
        arr[i] = temp[i];
    }
}

// Function to print elements of array
void PrintTheArray(int arr[], int n)
{
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
}

// Driver code
int main()
{
    int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
    int N = sizeof(arr) / sizeof(arr[0]);
    int d = 2;

    // Function calling
    Rotate(arr, d, N);
    PrintTheArray(arr, N);

    return 0;
}

Java

/*package whatever //do not write package name here */

import java.io.*;

class GFG {


// Function to rotate array
static void Rotate(int arr[], int d, int n)
{
    // Storing rotated version of array
    int temp[] = new int[n];

    // Keeping track of the current index
    // of temp[]
    int k = 0;

    // Storing the n - d elements of
    // array arr[] to the front of temp[]
    for (int i = d; i < n; i++) {
        temp[k] = arr[i];
        k++;
    }

    // Storing the first d elements of array arr[]
    //  into temp
    for (int i = 0; i < d; i++) {
        temp[k] = arr[i];
        k++;
    }

    // Copying the elements of temp[] in arr[]
    // to get the final rotated array
    for (int i = 0; i < n; i++) {
        arr[i] = temp[i];
    }
}

// Function to print elements of array
static void PrintTheArray(int arr[], int n)
{
    for (int i = 0; i < n; i++) {
        System.out.print(arr[i]+" ");
    }
}
    public static void main (String[] args) {
        int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
        int N = arr.length;
        int d = 2;

        // Function calling
        Rotate(arr, d, N);
        PrintTheArray(arr, N);
    }
}

// This code is contributed by ishankhandelwals.

Python3

def rotate(L, d, n):
    k = L.index(d)
    new_lis = []
    new_lis = L[k+1:]+L[0:k+1]
    return new_lis


if __name__ == '__main__':
    arr = [1, 2, 3, 4, 5, 6, 7]
    d = 2
    N = len(arr)

    # Function call
    arr = rotate(arr, d, N)
    for i in arr:
        print(i, end=" ")

C#

// Include namespace system
using System;

public class GFG
{
  // Function to rotate array
  public static void Rotate(int[] arr, int d, int n)
  {
    // Storing rotated version of array
    int[] temp = new int[n];

    // Keeping track of the current index
    // of temp[]
    var k = 0;
    // Storing the n - d elements of
    // array arr[] to the front of temp[]
    for (int i = d; i < n; i++)
    {
      temp[k] = arr[i];
      k++;
    }

    // Storing the first d elements of array arr[]
    //  into temp
    for (int i = 0; i < d; i++)
    {
      temp[k] = arr[i];
      k++;
    }

    // Copying the elements of temp[] in arr[]
    // to get the final rotated array
    for (int i = 0; i < n; i++)
    {
      arr[i] = temp[i];
    }
  }
  // Function to print elements of array
  public static void PrintTheArray(int[] arr, int n)
  {
    for (int i = 0; i < n; i++)
    {
      Console.Write(arr[i].ToString() + " ");
    }
  }
  public static void Main(String[] args)
  {
    int[] arr = {1, 2, 3, 4, 5, 6, 7};
    var N = arr.Length;
    var d = 2;

    // Function calling
    GFG.Rotate(arr, d, N);
    GFG.PrintTheArray(arr, N);
  }
}

// This code is contributed by ishankhandelwals.

Javascript

function Rotate_and_Print(arr,d,n)
 {
     //Initializing array temp with size n
     var temp=new Array(n);

    let k = 0;

    // Storing the n - d elements of
    // array arr[] to the front of temp[]
    for (let i = d; i < n; i++) {
        temp[k] = arr[i];
        k++;
    }

    // Storing the first d elements of array arr[]
    //  into temp
    for (let i = 0; i < d; i++) {
        temp[k] = arr[i];
        k++;
    }
    //Printing the temp array which stores the result
    for (let i = 0; i < n; i++) {
        console.log(temp[i]+" ");
    }
 }

let arr = [ 1, 2, 3, 4, 5, 6, 7 ];
let n = arr.length;
let d = 2; //number of times rotating the array
Rotate_and_Print(arr, d, n);

//contributed by keerthikarathan123

Output

3 4 5 6 7 1 2 

Time complexity: O(N) 
Auxiliary Space: O(N)

Approach 2 (Rotate one by one): This problem can be solved using the below idea:

• At each iteration, shift the elements by one position to the left circularly (i.e., first element becomes the last).
• Perform this operation d times to rotate the elements to the left by d position.

Illustration:

Let us take arr[] = [1, 2, 3, 4, 5, 6, 7], d = 2.

First Step:
        => Rotate to left by one position.
        => arr[] = {2, 3, 4, 5, 6, 7, 1}

Second Step:
        => Rotate again to left by one position
        => arr[] = {3, 4, 5, 6, 7, 1, 2}

Rotation is done by 2 times.
So the array becomes arr[] = {3, 4, 5, 6, 7, 1, 2}

Follow the steps below to solve the given problem.

• Rotate the array to left by one position. For that do the following:
  • Store the first element of the array in a temporary variable.
  • Shift the rest of the elements in the original array by one place.
  • Update the last index of the array with the temporary variable.
• Repeat the above steps for the number of left rotations required.

Below is the implementation of the above approach:

C++

// C++ program to rotate an array by
// d elements
#include <bits/stdc++.h>
using namespace std;

/*Function to left rotate arr[] of size n by d*/
void Rotate(int arr[], int d, int n)
{
    int p = 1;
    while (p <= d) {
        int last = arr[0];
        for (int i = 0; i < n - 1; i++) {
            arr[i] = arr[i + 1];
        }
        arr[n - 1] = last;
        p++;
    }
}

// Function to print an array
void printArray(int arr[], int size)
{
    for (int i = 0; i < size; i++)
        cout << arr[i] << " ";
}

// Driver code
int main()
{
    int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
    int N = sizeof(arr) / sizeof(arr[0]);
    int d = 2;

    // Function calling
    Rotate(arr, d, N);
    printArray(arr, N);

    return 0;
}

Java

/*package whatever //do not write package name here */

import java.io.*;

class GFG {

    public static void rotate(int arr[], int d, int n)
    {
        int p = 1;
        while (p <= d) {
            int last = arr[0];
            for (int i = 0; i < n - 1; i++) {
                arr[i] = arr[i + 1];
            }
            arr[n - 1] = last;
            p++;
        }

        for (int i = 0; i < n; i++) {
            System.out.print(arr[i] + " ");
        }
    }

    public static void main(String[] args)
    {
        int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
        int N = arr.length;
        // Rotate 2 times
        int d = 2;

        // Function call
        rotate(arr, d, N);
    }
}
// contributed by keerthikarathan123

Python3

# Python program to rotate an array by d elements

# Function to left rotate arr[] of size n by d
def Rotate(arr, d, n):
  p = 1
  while(p <= d):
    last = arr[0]
    for i in range (n - 1):
      arr[i] = arr[i + 1]
    arr[n - 1] = last
    p = p + 1

# Function to print an array
def printArray(arr, size):
  for i in range (size):
    print(arr[i] ,end = " ")

# Driver code
arr = [1, 2, 3, 4, 5, 6, 7]
N = len(arr)
d = 2

# Function calling
Rotate(arr, d, N)
printArray(arr, N)

# This code is contributed by Atul_kumar_Shrivastava

C#

// Include namespace system
using System;


public class GFG
{
    public static void rotate(int[] arr, int d, int n)
    {
        var p = 1;
        while (p <= d)
        {
            var last = arr[0];
            for (int i = 0; i < n - 1; i++)
            {
                arr[i] = arr[i + 1];
            }
            arr[n - 1] = last;
            p++;
        }
        for (int i = 0; i < n; i++)
        {
            Console.Write(arr[i].ToString() + " ");
        }
    }
    public static void Main(String[] args)
    {
        int[] arr = {1, 2, 3, 4, 5, 6, 7};
        var N = arr.Length;
        // Rotate 2 times
        var d = 2;
        // Function call
        GFG.rotate(arr, d, N);
    }
}

Javascript

function printArray(arr,n,d)
{
    let p = 1;
        while (p <= d) {
            let last = arr[0];
            for (let i = 0; i < n - 1; i++) {
                arr[i] = arr[i + 1];
            }
            arr[n - 1] = last;
            p++;
        }

        for (let i = 0; i < n; i++) {
            console.log(arr[i] + " ");
        }
}
let arr = [ 1, 2, 3, 4, 5, 6, 7 ];
let n = arr.length;
let d=2; //number of times rotating the array

// Function calling
printArray(arr, n,d);

//contributed by keerthikarathan123

Output

3 4 5 6 7 1 2 

Time Complexity: O(N * d)
Auxiliary Space: O(1)

Approach 3 (A Juggling Algorithm): This is an extension of method 2. 

Instead of moving one by one, divide the array into different sets where the number of sets is equal to the GCD of N and d (say X. So the elements which are X distance apart are part of a set) and rotate the elements within sets by 1 position to the left. 

• Calculate the GCD between the length and the distance to be moved.
• The elements are only shifted within the sets.
• We start with temp = arr[0] and keep moving arr[I+d] to arr[I] and finally store temp at the right place.

Follow the below illustration for a better understanding

Illustration:

Each steps looks like following:

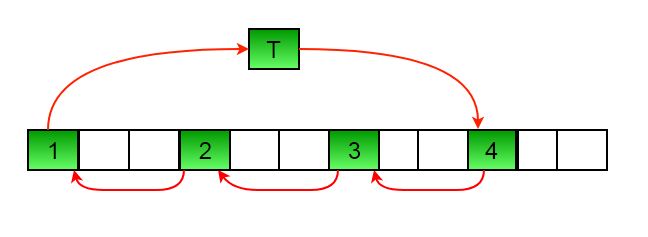
Let arr[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14} and d = 10

First step:
       => First set is {0, 5, 10}.
       => Rotate this set by d position in cyclic order
       => arr[0] = arr[0+10]
       => arr[10] = arr[(10+10)%15]
       => arr[5] = arr[0]
       => This set becomes {10,0,5}
       => Array arr[] = {10, 1, 2, 3, 4, 0, 6, 7, 8, 9, 5, 11, 12, 13, 14}

Second step:
       => Second set is {1, 6, 11}.
       => Rotate this set by d position in cyclic order.
       => This set becomes {11, 1, 6}
       => Array arr[] =  {10, 11, 2, 3, 4, 0, 1, 7, 8, 9, 5, 6, 12, 13, 14}

Third step:
       => Second set is {2, 7, 12}.
       => Rotate this set by d position in cyclic order.
       => This set becomes {12, 2, 7}
       => Array arr[] =  {10, 11, 12, 3, 4, 0, 1, 2, 8, 9, 5, 6, 7, 13, 14}

Fourth step:
       => Second set is {3, 8, 13}.
       => Rotate this set by d position in cyclic order.
       => This set becomes {13, 3, 8}
       => Array arr[] =  {10, 11, 12, 13, 4, 0, 1, 2, 3, 9, 5, 6, 7, 8, 14}

Fifth step:
       => Second set is {4, 9, 14}.
       => Rotate this set by d position in cyclic order.
       => This set becomes {14, 4, 9}
       => Array arr[] =  {10, 11, 12, 13, 14, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Follow the steps below to solve the given problem.

• Perform d%n in order to keep the value of d within the range of the array where d is the number of times the array is rotated and N is the size of the array.
• Calculate the GCD(N, d) to divide the array into sets.
• Run a for loop from 0 to the value obtained from GCD.
  • Store the value of arr[i] in a temporary variable (the value of i denotes the set number).
  • Run a while loop to update the values according to the set.
• After exiting the while loop assign the value of arr[j] as the value of the temporary variable (the value of j denotes the last element of the i^th set).

Below is the implementation of the above approach :

C++

// C++ program to rotate an array by
// d elements
#include <bits/stdc++.h>
using namespace std;

/*Function to get gcd of a and b*/
int gcd(int a, int b)
{
    if (b == 0)
        return a;

    else
        return gcd(b, a % b);
}

/*Function to left rotate arr[] of size n by d*/
void leftRotate(int arr[], int d, int n)
{
    /* To handle if d >= n */
    d = d % n;
    int g_c_d = gcd(d, n);
    for (int i = 0; i < g_c_d; i++) {
        /* move i-th values of blocks */
        int temp = arr[i];
        int j = i;

        while (1) {
            int k = j + d;
            if (k >= n)
                k = k - n;

            if (k == i)
                break;

            arr[j] = arr[k];
            j = k;
        }
        arr[j] = temp;
    }
}

// Function to print an array
void printArray(int arr[], int size)
{
    for (int i = 0; i < size; i++)
        cout << arr[i] << " ";
}

/* Driver program to test above functions */
int main()
{
    int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
    int n = sizeof(arr) / sizeof(arr[0]);

    // Function calling
    leftRotate(arr, 2, n);
    printArray(arr, n);

    return 0;
}

C

// C program to rotate an array by
// d elements
#include <stdio.h>

/* function to print an array */
void printArray(int arr[], int size);

/*Function to get gcd of a and b*/
int gcd(int a, int b);

/*Function to left rotate arr[] of size n by d*/
void leftRotate(int arr[], int d, int n)
{
    int i, j, k, temp;
    /* To handle if d >= n */
    d = d % n;
    int g_c_d = gcd(d, n);
    for (i = 0; i < g_c_d; i++) {
        /* move i-th values of blocks */
        temp = arr[i];
        j = i;
        while (1) {
            k = j + d;
            if (k >= n)
                k = k - n;
            if (k == i)
                break;
            arr[j] = arr[k];
            j = k;
        }
        arr[j] = temp;
    }
}

/*UTILITY FUNCTIONS*/
/* function to print an array */
void printArray(int arr[], int n)
{
    int i;
    for (i = 0; i < n; i++)
        printf("%d ", arr[i]);
}

/*Function to get gcd of a and b*/
int gcd(int a, int b)
{
    if (b == 0)
        return a;
    else
        return gcd(b, a % b);
}

/* Driver program to test above functions */
int main()
{
    int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
    leftRotate(arr, 2, 7);
    printArray(arr, 7);
    getchar();
    return 0;
}

Java

// Java program to rotate an array by
// d elements
import java.io.*;
class RotateArray {
    /*Function to left rotate arr[] of size n by d*/
    void leftRotate(int arr[], int d, int n)
    {
        /* To handle if d >= n */
        d = d % n;
        int i, j, k, temp;
        int g_c_d = gcd(d, n);
        for (i = 0; i < g_c_d; i++) {
            /* move i-th values of blocks */
            temp = arr[i];
            j = i;
            while (true) {
                k = j + d;
                if (k >= n)
                    k = k - n;
                if (k == i)
                    break;
                arr[j] = arr[k];
                j = k;
            }
            arr[j] = temp;
        }
    }

    /*UTILITY FUNCTIONS*/

    /* function to print an array */
    void printArray(int arr[], int size)
    {
        int i;
        for (i = 0; i < size; i++)
            System.out.print(arr[i] + " ");
    }

    /*Function to get gcd of a and b*/
    int gcd(int a, int b)
    {
        if (b == 0)
            return a;
        else
            return gcd(b, a % b);
    }

    // Driver program to test above functions
    public static void main(String[] args)
    {
        RotateArray rotate = new RotateArray();
        int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
        rotate.leftRotate(arr, 2, 7);
        rotate.printArray(arr, 7);
    }
}

// This code has been contributed by Mayank Jaiswal

Python3

# Python3 program to rotate an array by
# d elements
# Function to left rotate arr[] of size n by d


def leftRotate(arr, d, n):
    d = d % n
    g_c_d = gcd(d, n)
    for i in range(g_c_d):

        # move i-th values of blocks
        temp = arr[i]
        j = i
        while 1:
            k = j + d
            if k >= n:
                k = k - n
            if k == i:
                break
            arr[j] = arr[k]
            j = k
        arr[j] = temp

# UTILITY FUNCTIONS
# function to print an array


def printArray(arr, size):
    for i in range(size):
        print("% d" % arr[i], end=" ")

# Function to get gcd of a and b


def gcd(a, b):
    if b == 0:
        return a
    else:
        return gcd(b, a % b)


# Driver program to test above functions
arr = [1, 2, 3, 4, 5, 6, 7]
n = len(arr)
d = 2
leftRotate(arr, d, n)
printArray(arr, n)

# This code is contributed by Shreyanshi Arun

C#

// C# program for array rotation
using System;

class GFG {
    /* Function to left rotate arr[]
    of size n by d*/
    static void leftRotate(int[] arr, int d, int n)
    {
        int i, j, k, temp;
        /* To handle if d >= n */
        d = d % n;
        int g_c_d = gcd(d, n);
        for (i = 0; i < g_c_d; i++) {
            /* move i-th values of blocks */
            temp = arr[i];
            j = i;
            while (true) {
                k = j + d;
                if (k >= n)
                    k = k - n;
                if (k == i)
                    break;
                arr[j] = arr[k];
                j = k;
            }
            arr[j] = temp;
        }
    }

    /*UTILITY FUNCTIONS*/
    /* Function to print an array */
    static void printArray(int[] arr, int size)
    {
        for (int i = 0; i < size; i++)
            Console.Write(arr[i] + " ");
    }

    /* Function to get gcd of a and b*/
    static int gcd(int a, int b)
    {
        if (b == 0)
            return a;
        else
            return gcd(b, a % b);
    }

    // Driver code
    public static void Main()
    {
        int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
        leftRotate(arr, 2, 7);
        printArray(arr, 7);
    }
}

// This code is contributed by Sam007

Javascript

<script>

// JavaScript program to rotate an array by
// d elements

/*Function to get gcd of a and b*/
function gcd( a, b){
    if (b == 0)
        return a;
    else
        return gcd(b, a % b);
}

/*Function to left rotate arr[] of size n by d*/
function leftRotate(arr, d, n){
    /* To handle if d >= n */
    d = d % n;
    let g_c_d = gcd(d, n);
    for (let i = 0; i < g_c_d; i++) {
        /* move i-th values of blocks */
        let temp = arr[i];
        let j = i;

        while (1) {
            let k = j + d;
            if (k >= n)
                k = k - n;

            if (k == i)
                break;

            arr[j] = arr[k];
            j = k;
        }
        arr[j] = temp;
    }
}

// Function to print an array
function printArray(arr, size){
    for (let i = 0; i < size; i++)
        document.write(arr[i] +" ");
}

/* Driver program to test above functions */
let arr = [ 1, 2, 3, 4, 5, 6, 7 ];
let n = arr.length;
// Function calling
leftRotate(arr, 2, n);
printArray(arr, n);

</script>

Output

3 4 5 6 7 1 2 

Time complexity : O(N) 
Auxiliary Space : O(1)

Please see the following posts for other methods of array rotation: 
Block swap algorithm for array rotation
Reversal algorithm for array rotation
Please write comments if you find any bugs in the above programs/algorithms.