Affine space
Last Updated :
21 Sep, 2021
Affine spaces

Affine space
Affine space is the set E with vector space \vec{E} and a transitive and free action of the additive \vec{E} on set E. The elements of space A are called points. The vector space \vec{E} that is associated with affine space is known as free vectors and the action +: E * \vec{E} \rightarrow E satisfying the following conditions:
- Right Identity: a + 0 = a
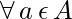
- Associativity:
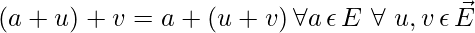
- For any two points a,b \epsilon E, there is unique u such that :
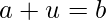
where u \epsilon \vec{E} and can be denoted ab or \vec{ab} or sometimes b-a. Therefore , we can write above equation
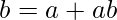
Example:
. Consider the subset L of 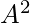 consisting of all points (x, y) satisfying the equation:
consisting of all points (x, y) satisfying the equation:
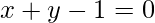
L is the line having slope -1 passing through the point (1,0) and (0,1). The line L can be an affine space by defining the action +: L * R \rightarrow L of R on L defined such that every point (x, 1-x) on L and any u \epsilon R.
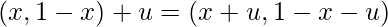
Now, for any two points a =(a_1, 1- a_1) and b = (b_1, 1-b_1) on L, the unique vector u \epsilon R such that b = a+u is u = b_1 – a_1. Note that vector space R isomorphic to the line of equation x + y = 0 passing through the origin.
Chasles’s Identity

Given any three points 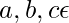 , since c = a + ac, b = a + ab, and c = b + bc, we get
, since c = a + ac, b = a + ab, and c = b + bc, we get
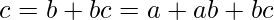
By applying the above properties 2 and 3,
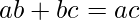
THe above equation is known as chasles Identity. Since
a = a + aa
and by using property 1 we,get
a = a+ 0
Thus, by using property 3, we get:
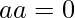
Replacing a in place of c in Chasles Identity, we get:
ba =-ab
Now, For 4 points a,b,c,d \epsilon E. The chasles identity can be given as:
ad+bc = ad+ dc = ac
Affine combinations/ Barycentres
Similar to linear combination in linear algebra, the corresponding concept in affine geometry is that of an affine combination, also called a barycenter
Consider 2-dimensional space as an affine space, with origin O= (0,0) and basis vectors (1,0) and (0,1). Given any two points a =(a1, a2) and b =(b1, b2) there can be a natural combination such that \lambda a+ \mu b or:
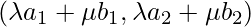
when a = (-1, -1) and b = (2, 2), thus a+b can be given as: c = (1,1).
Now, consider the new coordinate system with respect to the origin c = (1, 1). Now, the co-ordinates of a = (-2, -2), the co-ordinates of b are (1, 1), and the point of d = (-1, -1). However, point d is identical to the origin O = (0, 0) of the first coordinate system.
Thus, a + b corresponds to two different points depending on which coordinate system is used for its computation. This means that we need extra conditions are required for affine computations. It turns out the scalars sum up 1. This helps us define the Barycentres
For any family of points (a_i)_{i\epsilon I} in E, for any family of scalars such that 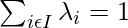 and for any
and for any 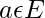 , the point
, the point
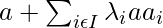 is called the barycentres of the points a_i assigned the weights
is called the barycentres of the points a_i assigned the weights 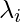 and is denoted by:
and is denoted by:
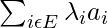 .
.
Barycentres is conveniently denoted by the notations 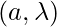 , whereas
, whereas 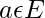 is a point and
is a point and 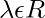 is called a scalar.
is called a scalar.
Affine Subspace
Given an affine space 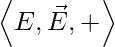 , a subset V of E is an affine subspace of
, a subset V of E is an affine subspace of 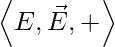 , if for every family of weighted points
, if for every family of weighted points 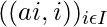 in V such that
in V such that 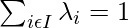 , the barycenter
, the barycenter 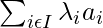 belongs to V .
belongs to V .
References:
Share your thoughts in the comments
Please Login to comment...