Search, Insert, and Delete in an Sorted Array | Array Operations
Last Updated :
05 Jul, 2023
How to Search in a Sorted Array?
In a sorted array, the search operation can be performed by using binary search.
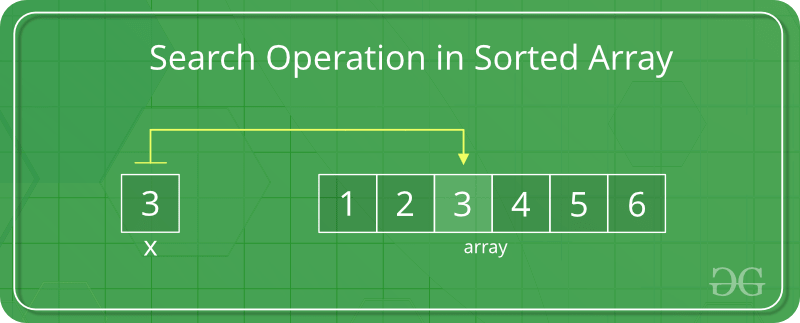
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int binarySearch(int arr[], int low, int high, int key)
{
if (high < low)
return -1;
int mid = (low + high) / 2;
if (key == arr[mid])
return mid;
if (key > arr[mid])
return binarySearch(arr, (mid + 1), high, key);
return binarySearch(arr, low, (mid - 1), key);
}
int main()
{
int arr[] = { 5, 6, 7, 8, 9, 10 };
int n, key;
n = sizeof(arr) / sizeof(arr[0]);
key = 10;
cout << "Index: " << binarySearch(arr, 0, n - 1, key)
<< endl;
return 0;
}
|
C
#include <stdio.h>
int binarySearch(int arr[], int low, int high, int key)
{
if (high < low)
return -1;
int mid = (low + high) / 2;
if (key == arr[mid])
return mid;
if (key > arr[mid])
return binarySearch(arr, (mid + 1), high, key);
return binarySearch(arr, low, (mid - 1), key);
}
int main()
{
int arr[] = { 5, 6, 7, 8, 9, 10 };
int n, key;
n = sizeof(arr) / sizeof(arr[0]);
key = 10;
printf("Index: %d\n", binarySearch(arr, 0, n - 1, key));
return 0;
}
|
Java
class Main {
static int binarySearch(int arr[], int low, int high,
int key)
{
if (high < low)
return -1;
int mid = (low + high) / 2;
if (key == arr[mid])
return mid;
if (key > arr[mid])
return binarySearch(arr, (mid + 1), high, key);
return binarySearch(arr, low, (mid - 1), key);
}
public static void main(String[] args)
{
int arr[] = { 5, 6, 7, 8, 9, 10 };
int n, key;
n = arr.length - 1;
key = 10;
System.out.println("Index: "
+ binarySearch(arr, 0, n, key));
}
}
|
Python3
def binarySearch(arr, low, high, key):
mid = (low + high)/2
if (key == arr[int(mid)]):
return mid
if (key > arr[int(mid)]):
return binarySearch(arr,
(mid + 1), high, key)
if (key < arr[int(mid)]):
return binarySearch(arr, low, (mid-1), key)
return 0
if __name__ == "__main__":
arr = [5, 6, 7, 8, 9, 10]
n = len(arr)
key = 10
print("Index:", int(binarySearch(arr, 0, n-1, key)))
|
C#
using System;
public class GFG {
public static int binarySearch(int[] arr, int low,
int high, int key)
{
if (high < low) {
return -1;
}
int mid = (low + high) / 2;
if (key == arr[mid]) {
return mid;
}
if (key > arr[mid]) {
return binarySearch(arr, (mid + 1), high, key);
}
return binarySearch(arr, low, (mid - 1), key);
}
public static void Main(string[] args)
{
int[] arr = new int[] { 5, 6, 7, 8, 9, 10 };
int n, key;
n = arr.Length;
key = 10;
Console.WriteLine(
"Index: " + binarySearch(arr, 0, n - 1, key));
}
}
|
PHP
<?php
function binarySearch($arr, $low,
$high, $key)
{
if ($high < $low)
return -1;
$mid = (int)($low + $high) / 2;
if ($key == $arr[(int)$mid])
return $mid;
if ($key > $arr[(int)$mid])
return binarySearch($arr, ($mid + 1),
$high, $key);
return (binarySearch($arr, $low,
($mid -1), $key));
}
$arr = array(5, 6, 7, 8, 9, 10);
$n = count($arr);
$key = 10;
echo "Index: ", (int)binarySearch($arr, 0,
$n-1, $key);
?>
|
Javascript
<script>
function binarySearch( arr, low, high, key)
{
if (high < low)
return -1;
let mid = Math.trunc((low + high) / 2);
if (key == arr[mid])
return mid;
if (key > arr[mid])
return binarySearch(arr, (mid + 1), high, key);
return binarySearch(arr, low, (mid - 1), key);
}
let arr = [ 5, 6, 7, 8, 9, 10 ];
let n, key;
n = arr.length;
key = 10;
document.write( "Index: " + binarySearch(arr, 0, n - 1, key)
+ "</br>");
</script>
|
Time Complexity: O(log(n)) Using Binary Search
Auxiliary Space: O(log(n)) due to recursive calls, otherwise iterative version uses Auxiliary Space of O(1).
How to Insert in a Sorted Array?
In a sorted array, a search operation is performed for the possible position of the given element by using Binary search, and then an insert operation is performed followed by shifting the elements. And in an unsorted array, the insert operation is faster as compared to the sorted array because we don’t have to care about the position at which the element is placed.

Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int insertSorted(int arr[], int n, int key, int capacity)
{
if (n >= capacity)
return n;
int i;
for (i = n - 1; (i >= 0 && arr[i] > key); i--)
arr[i + 1] = arr[i];
arr[i + 1] = key;
return (n + 1);
}
int main()
{
int arr[20] = { 12, 16, 20, 40, 50, 70 };
int capacity = sizeof(arr) / sizeof(arr[0]);
int n = 6;
int i, key = 26;
cout << "\nBefore Insertion: ";
for (i = 0; i < n; i++)
cout << arr[i] << " ";
n = insertSorted(arr, n, key, capacity);
cout << "\nAfter Insertion: ";
for (i = 0; i < n; i++)
cout << arr[i] << " ";
return 0;
}
|
C
#include <stdio.h>
int insertSorted(int arr[], int n, int key, int capacity)
{
if (n >= capacity)
return n;
int i;
for (i = n - 1; (i >= 0 && arr[i] > key); i--)
arr[i + 1] = arr[i];
arr[i + 1] = key;
return (n + 1);
}
int main()
{
int arr[20] = { 12, 16, 20, 40, 50, 70 };
int capacity = sizeof(arr) / sizeof(arr[0]);
int n = 6;
int i, key = 26;
printf("\nBefore Insertion: ");
for (i = 0; i < n; i++)
printf("%d ", arr[i]);
n = insertSorted(arr, n, key, capacity);
printf("\nAfter Insertion: ");
for (i = 0; i < n; i++)
printf("%d ", arr[i]);
return 0;
}
|
Java
class Main {
static int insertSorted(int arr[], int n, int key,
int capacity)
{
if (n >= capacity)
return n;
int i;
for (i = n - 1; (i >= 0 && arr[i] > key); i--)
arr[i + 1] = arr[i];
arr[i + 1] = key;
return (n + 1);
}
public static void main(String[] args)
{
int arr[] = new int[20];
arr[0] = 12;
arr[1] = 16;
arr[2] = 20;
arr[3] = 40;
arr[4] = 50;
arr[5] = 70;
int capacity = arr.length;
int n = 6;
int key = 26;
System.out.print("\nBefore Insertion: ");
for (int i = 0; i < n; i++)
System.out.print(arr[i] + " ");
n = insertSorted(arr, n, key, capacity);
System.out.print("\nAfter Insertion: ");
for (int i = 0; i < n; i++)
System.out.print(arr[i] + " ");
}
}
|
Python3
def insertSorted(arr, n, key, capacity):
if (n >= capacity):
return n
i = n - 1
while i >= 0 and arr[i] > key:
arr[i + 1] = arr[i]
i -= 1
arr[i + 1] = key
return (n + 1)
if __name__ == "__main__":
arr = [12, 16, 20, 40, 50, 70]
for i in range(20):
arr.append(0)
capacity = len(arr)
n = 6
key = 26
print("Before Insertion: ", end=" ")
for i in range(n):
print(arr[i], end=" ")
n = insertSorted(arr, n, key, capacity)
print("\nAfter Insertion: ", end="")
for i in range(n):
print(arr[i], end=" ")
|
C#
using System;
public class GFG {
public static int insertSorted(int[] arr, int n,
int key, int capacity)
{
if (n >= capacity) {
return n;
}
int i;
for (i = n - 1; (i >= 0 && arr[i] > key); i--) {
arr[i + 1] = arr[i];
}
arr[i + 1] = key;
return (n + 1);
}
public static void Main(string[] args)
{
int[] arr = new int[20];
arr[0] = 12;
arr[1] = 16;
arr[2] = 20;
arr[3] = 40;
arr[4] = 50;
arr[5] = 70;
int capacity = arr.Length;
int n = 6;
int key = 26;
Console.Write("\nBefore Insertion: ");
for (int i = 0; i < n; i++) {
Console.Write(arr[i] + " ");
}
n = insertSorted(arr, n, key, capacity);
Console.Write("\nAfter Insertion: ");
for (int i = 0; i < n; i++) {
Console.Write(arr[i] + " ");
}
}
}
|
Javascript
<script>
function insertSorted( arr, n, key, capacity)
{
if (n >= capacity)
return n;
var i;
for (i = n - 1; (i >= 0 && arr[i] > key); i--)
arr[i + 1] = arr[i];
arr[i + 1] = key;
return (n + 1);
}
var arr = new Array(20);
arr[0] = 12;
arr[1] = 16;
arr[2] = 20;
arr[3] = 40;
arr[4] = 50;
arr[5] = 70;
var capacity = arr.length;
var n = 6;
var key = 26;
document.write("\nBefore Insertion: ");
for (var i = 0; i < n; i++)
document.write(arr[i] + " ");
n = insertSorted(arr, n, key, capacity);
document.write("<br>" +"\nAfter Insertion: ");
for (var i = 0; i < n; i++)
document.write(arr[i] + " ");
</script>
|
Output
Before Insertion: 12 16 20 40 50 70
After Insertion: 12 16 20 26 40 50 70
Time Complexity: O(N) [In the worst case all elements may have to be moved]
Auxiliary Space: O(1)
How to Delete in a Sorted Array?
In the delete operation, the element to be deleted is searched using binary search, and then the delete operation is performed followed by shifting the elements.
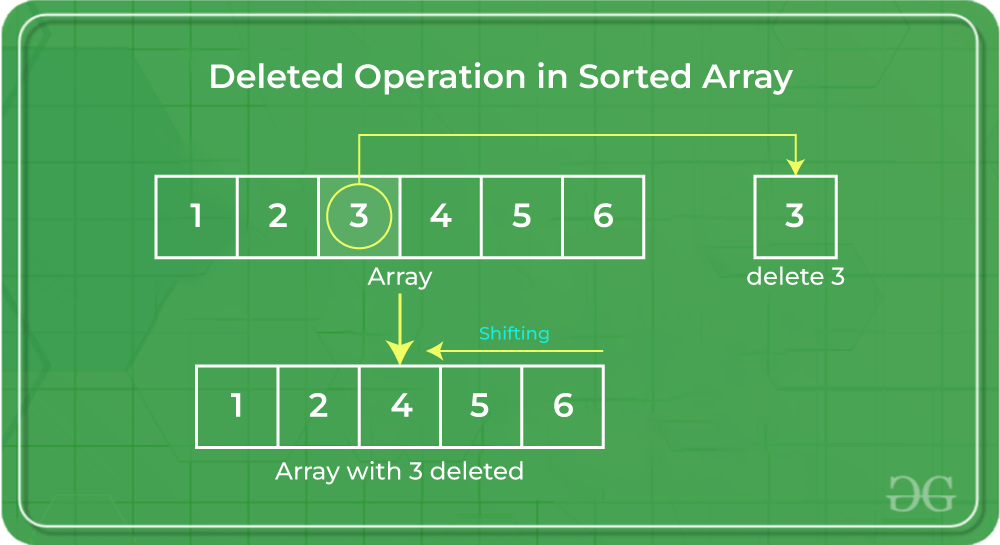
Performing delete operation
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int binarySearch(int arr[], int low, int high, int key);
int deleteElement(int arr[], int n, int key)
{
int pos = binarySearch(arr, 0, n - 1, key);
if (pos == -1) {
cout << "Element not found";
return n;
}
int i;
for (i = pos; i < n - 1; i++)
arr[i] = arr[i + 1];
return n - 1;
}
int binarySearch(int arr[], int low, int high, int key)
{
if (high < low)
return -1;
int mid = (low + high) / 2;
if (key == arr[mid])
return mid;
if (key > arr[mid])
return binarySearch(arr, (mid + 1), high, key);
return binarySearch(arr, low, (mid - 1), key);
}
int main()
{
int i;
int arr[] = { 10, 20, 30, 40, 50 };
int n = sizeof(arr) / sizeof(arr[0]);
int key = 30;
cout << "Array before deletion\n";
for (i = 0; i < n; i++)
cout << arr[i] << " ";
n = deleteElement(arr, n, key);
cout << "\n\nArray after deletion\n";
for (i = 0; i < n; i++)
cout << arr[i] << " ";
}
|
C
#include <stdio.h>
int binarySearch(int arr[], int low, int high, int key);
int deleteElement(int arr[], int n, int key)
{
int pos = binarySearch(arr, 0, n - 1, key);
if (pos == -1) {
printf("Element not found");
return n;
}
int i;
for (i = pos; i < n - 1; i++)
arr[i] = arr[i + 1];
return n - 1;
}
int binarySearch(int arr[], int low, int high, int key)
{
if (high < low)
return -1;
int mid = (low + high) / 2;
if (key == arr[mid])
return mid;
if (key > arr[mid])
return binarySearch(arr, (mid + 1), high, key);
return binarySearch(arr, low, (mid - 1), key);
}
int main()
{
int i;
int arr[] = { 10, 20, 30, 40, 50 };
int n = sizeof(arr) / sizeof(arr[0]);
int key = 30;
printf("Array before deletion\n");
for (i = 0; i < n; i++)
printf("%d ", arr[i]);
n = deleteElement(arr, n, key);
printf("\n\nArray after deletion\n");
for (i = 0; i < n; i++)
printf("%d ", arr[i]);
}
|
Java
class Main {
static int binarySearch(int arr[], int low, int high,
int key)
{
if (high < low)
return -1;
int mid = (low + high) / 2;
if (key == arr[mid])
return mid;
if (key > arr[mid])
return binarySearch(arr, (mid + 1), high, key);
return binarySearch(arr, low, (mid - 1), key);
}
static int deleteElement(int arr[], int n, int key)
{
int pos = binarySearch(arr, 0, n - 1, key);
if (pos == -1) {
System.out.println("Element not found");
return n;
}
int i;
for (i = pos; i < n - 1; i++)
arr[i] = arr[i + 1];
return n - 1;
}
public static void main(String[] args)
{
int i;
int arr[] = { 10, 20, 30, 40, 50 };
int n = arr.length;
int key = 30;
System.out.print("Array before deletion:\n");
for (i = 0; i < n; i++)
System.out.print(arr[i] + " ");
n = deleteElement(arr, n, key);
System.out.print("\n\nArray after deletion:\n");
for (i = 0; i < n; i++)
System.out.print(arr[i] + " ");
}
}
|
Python3
def deleteElement(arr, n, key):
pos = binarySearch(arr, 0, n - 1, key)
if (pos == -1):
print("Element not found")
return n
for i in range(pos, n - 1):
arr[i] = arr[i + 1]
return n - 1
def binarySearch(arr, low, high, key):
if (high < low):
return -1
mid = (low + high) // 2
if (key == arr[mid]):
return mid
if (key > arr[mid]):
return binarySearch(arr, (mid + 1), high, key)
return binarySearch(arr, low, (mid - 1), key)
if __name__ == "__main__":
arr = [10, 20, 30, 40, 50]
n = len(arr)
key = 30
print("Array before deletion")
for i in range(n):
print(arr[i], end=" ")
n = deleteElement(arr, n, key)
print("\n\nArray after deletion")
for i in range(n):
print(arr[i], end=" ")
|
C#
using System;
public class GFG {
static int binarySearch(int[] arr, int low, int high,
int key)
{
if (high < low)
return -1;
int mid = (low + high) / 2;
if (key == arr[mid])
return mid;
if (key > arr[mid])
return binarySearch(arr, (mid + 1), high, key);
return binarySearch(arr, low, (mid - 1), key);
}
static int deleteElement(int[] arr, int n, int key)
{
int pos = binarySearch(arr, 0, n - 1, key);
if (pos == -1) {
Console.WriteLine("Element not found");
return n;
}
int i;
for (i = pos; i < n - 1; i++)
arr[i] = arr[i + 1];
return n - 1;
}
public static void Main()
{
int i;
int[] arr = { 10, 20, 30, 40, 50 };
int n = arr.Length;
int key = 30;
Console.Write("Array before deletion:\n");
for (i = 0; i < n; i++)
Console.Write(arr[i] + " ");
n = deleteElement(arr, n, key);
Console.Write("\n\nArray after deletion:\n");
for (i = 0; i < n; i++)
Console.Write(arr[i] + " ");
}
}
|
Javascript
<script>
function binarySearch(arr, low, high, key)
{
if (high < low)
return -1;
let mid = (low + high) / 2;
if (key == arr[mid])
return mid;
if (key > arr[mid])
return binarySearch(arr, (mid + 1), high, key);
return binarySearch(arr, low, (mid - 1), key);
}
function deleteElement( arr, n, key)
{
let pos = binarySearch(arr, 0, n - 1, key);
if (pos == -1) {
document.write("Element not found");
return n;
}
let i;
for (i = pos; i < n - 1; i++)
arr[i] = arr[i + 1];
return n - 1;
}
let i;
let arr = [ 10, 20, 30, 40, 50 ];
let n = arr.length;
let key = 30;
document.write("Array before deletion:\n");
for (i = 0; i < n; i++)
document.write(arr[i] + " ");
n = deleteElement(arr, n, key);
document.write("<br>"+"Array after deletion:\n");
for (i = 0; i < n; i++)
document.write(arr[i] + " ");
</script>
|
Output
Array before deletion
10 20 30 40 50
Array after deletion
10 20 40 50
Time Complexity: O(N). In the worst case all elements may have to be moved
Auxiliary Space: O(log N). An implicit stack will be used
Share your thoughts in the comments
Please Login to comment...