Euler’s Totient function Φ(n) for an input n is the count of numbers in {1, 2, 3, …, n-1} that are relatively prime to n, i.e., the numbers whose GCD (Greatest Common Divisor) with n is 1.
Examples :
Φ(1) = 1
gcd(1, 1) is 1
Φ(2) = 1
gcd(1, 2) is 1, but gcd(2, 2) is 2.
Φ(3) = 2
gcd(1, 3) is 1 and gcd(2, 3) is 1
Φ(4) = 2
gcd(1, 4) is 1 and gcd(3, 4) is 1
Φ(5) = 4
gcd(1, 5) is 1, gcd(2, 5) is 1,
gcd(3, 5) is 1 and gcd(4, 5) is 1
Φ(6) = 2
gcd(1, 6) is 1 and gcd(5, 6) is 1,
How to compute Φ(n) for an input n?
A simple solution is to iterate through all numbers from 1 to n-1 and count numbers with gcd with n as 1. Below is the implementation of the simple method to compute Euler’s Totient function for an input integer n.
C
// A simple C program to calculate Euler's Totient Function
#include <stdio.h>
// Function to return gcd of a and b
int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate Euler Totient Function
int phi(unsigned int n)
{
unsigned int result = 1;
for (int i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver program to test above function
int main()
{
int n;
for (n = 1; n <= 10; n++)
printf("phi(%d) = %d\n", n, phi(n));
return 0;
}
// A simple java program to calculate
// Euler's Totient Function
import java.io.*;
class GFG {
// Function to return GCD of a and b
static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate
// Euler Totient Function
static int phi(int n)
{
int result = 1;
for (int i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver code
public static void main(String[] args)
{
int n;
for (n = 1; n <= 10; n++)
System.out.println("phi(" + n + ") = " + phi(n));
}
}
// This code is contributed by sunnusingh
# A simple Python3 program
# to calculate Euler's
# Totient Function
# Function to return
# gcd of a and b
def gcd(a, b):
if (a == 0):
return b
return gcd(b % a, a)
# A simple method to evaluate
# Euler Totient Function
def phi(n):
result = 1
for i in range(2, n):
if (gcd(i, n) == 1):
result+=1
return result
# Driver Code
for n in range(1, 11):
print("phi(",n,") = ",
phi(n), sep = "")
# This code is contributed
# by Smitha
// A simple C# program to calculate
// Euler's Totient Function
using System;
class GFG {
// Function to return GCD of a and b
static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate
// Euler Totient Function
static int phi(int n)
{
int result = 1;
for (int i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver code
public static void Main()
{
for (int n = 1; n <= 10; n++)
Console.WriteLine("phi(" + n + ") = " + phi(n));
}
}
// This code is contributed by nitin mittal
<script>
// Javascript program to calculate
// Euler's Totient Function
// Function to return
// gcd of a and b
function gcd(a, b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate
// Euler Totient Function
function phi(n)
{
let result = 1;
for (let i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver Code
for (let n = 1; n <= 10; n++)
document.write(`phi(${n}) = ${phi(n)} <br>`);
// This code is contributed by _saurabh_jaiswal
</script>
<Φphp
// PHP program to calculate
// Euler's Totient Function
// Function to return
// gcd of a and b
function gcd($a, $b)
{
if ($a == 0)
return $b;
return gcd($b % $a, $a);
}
// A simple method to evaluate
// Euler Totient Function
function phi($n)
{
$result = 1;
for ($i = 2; $i < $n; $i++)
if (gcd($i, $n) == 1)
$result++;
return $result;
}
// Driver Code
for ($n = 1; $n <= 10; $n++)
echo "phi(" .$n. ") =" . phi($n)."\n";
// This code is contributed by Sam007
Φ>
// A simple C++ program to calculate
// Euler's Totient Function
#include <iostream>
using namespace std;
// Function to return gcd of a and b
int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate Euler Totient Function
int phi(unsigned int n)
{
unsigned int result = 1;
for (int i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver program to test above function
int main()
{
int n;
for (n = 1; n <= 10; n++)
cout << "phi("<<n<<") = " << phi(n) << endl;
return 0;
}
// This code is contributed by SHUBHAMSINGH10
Outputphi(1) = 1
phi(2) = 1
phi(3) = 2
phi(4) = 2
phi(5) = 4
phi(6) = 2
phi(7) = 6
phi(8) = 4
phi(9) = 6
phi(10) = 4
The above code calls gcd function O(n) times. The time complexity of the gcd function is O(h) where “h” is the number of digits in a smaller number of given two numbers. Therefore, an upper bound on the time complexity of the above solution is O(N^2 log N) [How Φ there can be at most Log10n digits in all numbers from 1 to n]
Auxiliary Space: O(log N)
Below is a Better Solution. The idea is based on Euler’s product formula which states that the value of totient functions is below the product overall prime factors p of n.
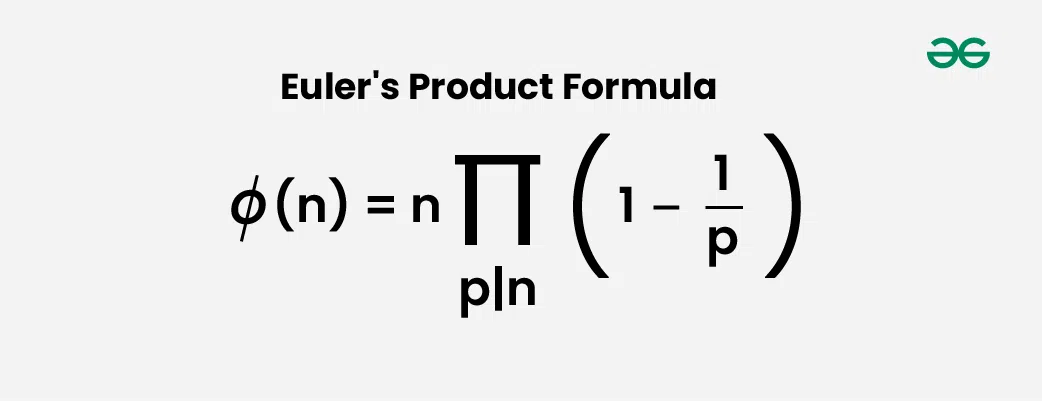
The formula basically says that the value of Φ(n) is equal to n multiplied by-product of (1 – 1/p) for all prime factors p of n. For example value of Φ(6) = 6 * (1-1/2) * (1 – 1/3) = 2.
We can find all prime factors using the idea used in this post.
1) Initialize : result = n
2) Run a loop from 'p' = 2 to sqrt(n), do following for every 'p'.
a) If p divides n, then
Set: result = result * (1.0 - (1.0 / (float) p));
Divide all occurrences of p in n.
3) Return result
Below is the implementation of Euler’s product formula.
C++
// C++ program to calculate Euler's
// Totient Function using Euler's
// product formula
#include <bits/stdc++.h>
using namespace std;
int phi(int n)
{
// Initialize result as n
float result = n;
// Consider all prime factors of n
// and for every prime factor p,
// multiply result with (1 - 1/p)
for(int p = 2; p * p <= n; ++p)
{
// Check if p is a prime factor.
if (n % p == 0)
{
// If yes, then update n and result
while (n % p == 0)
n /= p;
result *= (1.0 - (1.0 / (float)p));
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result -= result / n;
//Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
//if n is a prime number
return (int)result;
}
// Driver code
int main()
{
int n;
for(n = 1; n <= 10; n++)
{
cout << "Phi" << "("
<< n << ")" << " = "
<< phi(n) <<endl;
}
return 0;
}
// This code is contributed by koulick_sadhu
// C program to calculate Euler's Totient Function
// using Euler's product formula
#include <stdio.h>
int phi(int n)
{
float result = n; // Initialize result as n
// Consider all prime factors of n and for every prime
// factor p, multiply result with (1 - 1/p)
for (int p = 2; p * p <= n; ++p) {
// Check if p is a prime factor.
if (n % p == 0) {
// If yes, then update n and result
while (n % p == 0)
n /= p;
result *= (1.0 - (1.0 / (float)p));
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result -= result / n;
//Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
//if n is a prime number
return (int)result;
}
// Driver program to test above function
int main()
{
int n;
for (n = 1; n <= 10; n++)
printf("phi(%d) = %d\n", n, phi(n));
return 0;
}
// Java program to calculate Euler's Totient
// Function using Euler's product formula
import java.io.*;
class GFG {
static int phi(int n)
{
// Initialize result as n
float result = n;
// Consider all prime factors of n and for
// every prime factor p, multiply result
// with (1 - 1/p)
for (int p = 2; p * p <= n; ++p) {
// Check if p is a prime factor.
if (n % p == 0) {
// If yes, then update n and result
while (n % p == 0)
n /= p;
result *= (1.0 - (1.0 / (float)p));
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result -= result / n;
//Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
//if n is a prime number
return (int)result;
}
// Driver program to test above function
public static void main(String args[])
{
int n;
for (n = 1; n <= 10; n++)
System.out.println("phi(" + n + ") = " + phi(n));
}
}
// This code is contributed by Nikita Tiwari.
# Python 3 program to calculate
# Euler's Totient Function
# using Euler's product formula
def phi(n) :
result = n # Initialize result as n
# Consider all prime factors
# of n and for every prime
# factor p, multiply result with (1 - 1 / p)
p = 2
while p * p<= n :
# Check if p is a prime factor.
if n % p == 0 :
# If yes, then update n and result
while n % p == 0 :
n = n // p
result = result * (1.0 - (1.0 / float(p)))
p = p + 1
# If n has a prime factor
# greater than sqrt(n)
# (There can be at-most one
# such prime factor)
if n > 1 :
result -= result // n
#Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
#if n is a prime number
return int(result)
# Driver program to test above function
for n in range(1, 11) :
print("phi(", n, ") = ", phi(n))
# This code is contributed
# by Nikita Tiwari.
// C# program to calculate Euler's Totient
// Function using Euler's product formula
using System;
class GFG {
static int phi(int n)
{
// Initialize result as n
float result = n;
// Consider all prime factors
// of n and for every prime
// factor p, multiply result
// with (1 - 1 / p)
for (int p = 2; p * p <= n; ++p)
{
// Check if p is a prime factor.
if (n % p == 0)
{
// If yes, then update
// n and result
while (n % p == 0)
n /= p;
result *= (float)(1.0 - (1.0 / (float)p));
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if (n > 1)
result -= result / n;
//Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
//if n is a prime number
return (int)result;
}
// Driver Code
public static void Main()
{
int n;
for (n = 1; n <= 10; n++)
Console.WriteLine("phi(" + n + ") = " + phi(n));
}
}
// This code is contributed by nitin mittal.
// Javascript program to calculate
// Euler's Totient Function
// using Euler's product formula
function phi(n)
{
// Initialize result as n
let result = n;
// Consider all prime factors
// of n and for every prime
// factor p, multiply result
// with (1 - 1/p)
for (let p = 2; p * p <= n; ++p)
{
// Check if p is
// a prime factor.
if (n % p == 0)
{
// If yes, then update
// n and result
while (n % p == 0)
n /= p;
result *= (1.0 - (1.0 / p));
}
}
// If n has a prime factor greater
// than sqrt(n) (There can be at-most
// one such prime factor)
if (n > 1)
result -= result / n;
//Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
//if n is a prime number
return parseInt(result);
}
// Driver Code
for (let n = 1; n <= 10; n++)
document.write(`phi(${n}) = ${phi(n)} <br>`);
// This code is contributed by _saurabh_jaiswal
<Φphp
// PHP program to calculate
// Euler's Totient Function
// using Euler's product formula
function phi($n)
{
// Initialize result as n
$result = $n;
// Consider all prime factors
// of n and for every prime
// factor p, multiply result
// with (1 - 1/p)
for ($p = 2; $p * $p <= $n; ++$p)
{
// Check if p is
// a prime factor.
if ($n % $p == 0)
{
// If yes, then update
// n and result
while ($n % $p == 0)
$n /= $p;
$result *= (1.0 - (1.0 / $p));
}
}
// If n has a prime factor greater
// than sqrt(n) (There can be at-most
// one such prime factor)
if ($n > 1)
$result -= $result / $n;
//Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
//if n is a prime number
return intval($result);
}
// Driver Code
for ($n = 1; $n <= 10; $n++)
echo "phi(" .$n. ") =" . phi($n)."\n";
// This code is contributed by Sam007
Φ>
OutputPhi(1) = 1
Phi(2) = 1
Phi(3) = 2
Phi(4) = 2
Phi(5) = 4
Phi(6) = 2
Phi(7) = 6
Phi(8) = 4
Phi(9) = 6
Phi(10) = 4
Time Complexity: O(Φ n log n)
Auxiliary Space: O(1)
We can avoid floating-point calculations in the above method. The idea is to count all prime factors and their multiples and subtract this count from n to get the totient function value (Prime factors and multiples of prime factors won’t have gcd as 1)
1) Initialize result as n
2) Consider every number 'p' (where 'p' varies from 2 to Φ(n)).
If p divides n, then do following
a) Subtract all multiples of p from 1 to n [all multiples of p
will have gcd more than 1 (at least p) with n]
b) Update n by repeatedly dividing it by p.
3) If the reduced n is more than 1, then remove all multiples
of n from result.
Below is the implementation of the above algorithm.
C++
// C++ program to calculate Euler's
// Totient Function
#include <bits/stdc++.h>
using namespace std;
int phi(int n)
{
// Initialize result as n
int result = n;
// Consider all prime factors of n
// and subtract their multiples
// from result
for(int p = 2; p * p <= n; ++p)
{
// Check if p is a prime factor.
if (n % p == 0)
{
// If yes, then update n and result
while (n % p == 0)
n /= p;
result -= result / p;
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result -= result / n;
return result;
}
// Driver code
int main()
{
int n;
for(n = 1; n <= 10; n++)
{
cout << "Phi" << "("
<< n << ")" << " = "
<< phi(n) << endl;
}
return 0;
}
// This code is contributed by koulick_sadhu
// C program to calculate Euler's Totient Function
#include <stdio.h>
int phi(int n)
{
int result = n; // Initialize result as n
// Consider all prime factors of n and subtract their
// multiples from result
for (int p = 2; p * p <= n; ++p) {
// Check if p is a prime factor.
if (n % p == 0) {
// If yes, then update n and result
while (n % p == 0)
n /= p;
result -= result / p;
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result -= result / n;
return result;
}
// Driver program to test above function
int main()
{
int n;
for (n = 1; n <= 10; n++)
printf("phi(%d) = %d\n", n, phi(n));
return 0;
}
// Java program to calculate
// Euler's Totient Function
import java.io.*;
class GFG
{
static int phi(int n)
{
// Initialize result as n
int result = n;
// Consider all prime factors
// of n and subtract their
// multiples from result
for (int p = 2; p * p <= n; ++p)
{
// Check if p is
// a prime factor.
if (n % p == 0)
{
// If yes, then update
// n and result
while (n % p == 0)
n /= p;
result -= result / p;
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if (n > 1)
result -= result / n;
return result;
}
// Driver Code
public static void main (String[] args)
{
int n;
for (n = 1; n <= 10; n++)
System.out.println("phi(" + n +
") = " + phi(n));
}
}
// This code is contributed by ajit
# Python3 program to calculate
# Euler's Totient Function
def phi(n):
# Initialize result as n
result = n;
# Consider all prime factors
# of n and subtract their
# multiples from result
p = 2;
while(p * p <= n):
# Check if p is a
# prime factor.
if (n % p == 0):
# If yes, then
# update n and result
while (n % p == 0):
n = int(n / p);
result -= int(result / p);
p += 1;
# If n has a prime factor
# greater than sqrt(n)
# (There can be at-most
# one such prime factor)
if (n > 1):
result -= int(result / n);
return result;
# Driver Code
for n in range(1, 11):
print("phi(",n,") =", phi(n));
# This code is contributed
# by mits
// C# program to calculate
// Euler's Totient Function
using System;
class GFG
{
static int phi(int n)
{
// Initialize result as n
int result = n;
// Consider all prime
// factors of n and
// subtract their
// multiples from result
for (int p = 2;
p * p <= n; ++p)
{
// Check if p is
// a prime factor.
if (n % p == 0)
{
// If yes, then update
// n and result
while (n % p == 0)
n /= p;
result -= result / p;
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if (n > 1)
result -= result / n;
return result;
}
// Driver Code
static public void Main ()
{
int n;
for (n = 1; n <= 10; n++)
Console.WriteLine("phi(" + n +
") = " +
phi(n));
}
}
// This code is contributed
// by akt_mit
// Javascript program to calculate
// Euler's Totient Function
function phi(n)
{
// Initialize
// result as n
let result = n;
// Consider all prime
// factors of n and subtract
// their multiples from result
for (let p = 2;
p * p <= n; ++p)
{
// Check if p is
// a prime factor.
if (n % p == 0)
{
// If yes, then
// update n and result
while (n % p == 0)
n = parseInt(n / p);
result -= parseInt(result / p);
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if (n > 1)
result -= parseInt(result / n);
return result;
}
// Driver Code
for (let n = 1; n <= 10; n++)
document.write(`phi(${n}) = ${phi(n)} <br>`);
// This code is contributed
// by _saurabh_jaiswal
<Φphp
// PHP program to calculate
// Euler's Totient Function
function phi($n)
{
// Initialize
// result as n
$result = $n;
// Consider all prime
// factors of n and subtract
// their multiples from result
for ($p = 2;
$p * $p <= $n; ++$p)
{
// Check if p is
// a prime factor.
if ($n % $p == 0)
{
// If yes, then
// update n and result
while ($n % $p == 0)
$n = (int)$n / $p;
$result -= (int)$result / $p;
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if ($n > 1)
$result -= (int)$result / $n;
return $result;
}
// Driver Code
for ($n = 1; $n <= 10; $n++)
echo "phi(", $n,") =",
phi($n), "\n";
// This code is contributed
// by ajit
Φ>
OutputPhi(1) = 1
Phi(2) = 1
Phi(3) = 2
Phi(4) = 2
Phi(5) = 4
Phi(6) = 2
Phi(7) = 6
Phi(8) = 4
Phi(9) = 6
Phi(10) = 4
Time Complexity: O(Φ n log n)
Auxiliary Space: O(1)
Let us take an example to understand the above algorithm.
n = 10.
Initialize: result = 10
2 is a prime factor, so n = n/i = 5, result = 5
3 is not a prime factor.
The for loop stops after 3 as 4*4 is not less than or equal
to 10.
After for loop, result = 5, n = 5
Since n > 1, result = result - result/n = 4
Some Interesting Properties of Euler’s Totient Function
1) For a prime number p, [Tex]\phi(p) = p – 1[/Tex]
Proof :
[Tex]\phi(p) = p - 1[/Tex] , where p is any prime numberWe know that [Tex]gcd(p, k) = 1[/Tex] where k is any random number and [Tex]k \neq p[/Tex][Tex]\\[/Tex]Total number from 1 to p = p Number for which [Tex]gcd(p, k) = 1[/Tex] is [Tex]1[/Tex], i.e the number p itself, so subtracting 1 from p [Tex]\phi(p) = p - 1[/Tex]
Examples :
[Tex]\phi(5) = 5 - 1 = 4[/Tex][Tex]\\[/Tex][Tex]\phi(13) = 13 - 1 = 12[/Tex][Tex]\\[/Tex][Tex]\phi(29) = 29 - 1 = 28[/Tex]
2) For two prime numbers a and b[Tex] \phi(a \cdot b) = \phi(a) \cdot \phi(b) = (a – 1) \cdot (b – 1) [/Tex], used in RSA Algorithm
Proof :
[Tex]\phi(a\cdot b) = \phi(a) \cdot \phi(b)[/Tex], where a and b are prime numbers[Tex]\phi(a) = a - 1[/Tex] , [Tex]\phi(b) = b - 1[/Tex][Tex]\\[/Tex]Total number from 1 to ab = ab Total multiples of a from 1 to ab = [Tex]\frac{a \cdot b} {a}[/Tex] = [Tex]b[/Tex]Total multiples of b from 1 to ab = [Tex]\frac{a \cdot b} {b}[/Tex] = [Tex]a[/Tex]Example:a = 5, b = 7, ab = 35Multiples of a = [Tex]\frac {35} {5}[/Tex] = 7 {5, 10, 15, 20, 25, 30, 35}Multiples of b = [Tex]\frac {35} {7}[/Tex] = 5 {7, 14, 21, 28, 35}[Tex]\\[/Tex]Can there be any double counting ?(watch above example carefully, try with other prime numbers also for more grasp)Ofcourse, we have counted [Tex]ab[/Tex] twice in multiples of a and multiples of b so, Total multiples = a + b - 1 (with which [Tex]gcd \neq 1[/Tex] with [Tex]ab[/Tex])[Tex]\\[/Tex][Tex]\phi(ab) = ab - (a + b - 1)[/Tex] , removing all number with [Tex]gcd \neq 1[/Tex] with [Tex]ab[/Tex] [Tex]\phi(ab) = a(b - 1) - (b - 1)[/Tex][Tex]\phi(ab) = (a - 1) \cdot (b - 1)[/Tex][Tex]\phi(ab) = \phi(a) \cdot \phi(b)[/Tex]
Examples :
[Tex]\phi(5 \cdot 7) = \phi(5) \cdot \phi(7) = (5 - 1) \cdot (7 - 1) = 24[/Tex][Tex]\\[/Tex][Tex]\phi(3 \cdot 5) = \phi(3) \cdot \phi(5) = (3 - 1) \cdot (5 - 1) = 8[/Tex][Tex]\\[/Tex][Tex]\phi(3 \cdot 7) = \phi(3) \cdot \phi(7) = (3 - 1) \cdot (7 - 1) = 12[/Tex]
3) For a prime number p, [Tex]\phi(p ^ k) = p ^ k – p ^ {k – 1}[/Tex]
Proof :
[Tex]\phi(p^k) = p ^ k - p ^{k - 1}[/Tex] , where p is a prime number[Tex]\\[/Tex]Total numbers from 1 to [Tex]p ^ k = p ^ k[/Tex] Total multiples of [Tex]p = \frac {p ^ k} {p} = p ^ {k - 1}[/Tex]Removing these multiples as with them [Tex]gcd \neq 1[/Tex][Tex]\\[/Tex]Example : p = 2, k = 5, [Tex]p ^ k[/Tex] = 32Multiples of 2 (as with them [Tex]gcd \neq 1[/Tex]) = 32 / 2 = 16 {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32}[Tex]\\[/Tex][Tex]\phi(p ^ k) = p ^ k - p ^ {k - 1}[/Tex]
Examples :
[Tex]\phi(2 ^ 5) = 2 ^ 5 - 2 ^ {5 - 1} = 32 - 16 = 16[/Tex][Tex]\\[/Tex][Tex]\phi(5 ^ 3) = 5 ^ 3 - 5 ^ {3 - 1} = 125 - 25 = 100[/Tex][Tex]\\[/Tex][Tex]\phi(3 ^ 5) = 3 ^ 5 - 3 ^ {5 - 1} = 243 - 81 = 162[/Tex]
4) For two number a and b [Tex]\phi(a \cdot b) [/Tex] [Tex]= \phi(a) \cdot \phi(b) [/Tex] [Tex]\cdot \frac {gcd(a, b)} {\phi(gcd(a, b))}[/Tex]
Special Case : gcd(a, b) = 1
[Tex]\phi(a \cdot b) = \phi(a) \cdot \phi(b) \cdot \frac {1} {\phi(1)} = \phi(a) \cdot \phi(b)[/Tex]
Examples :
Special Case : [Tex]gcd(a, b) = 1[/Tex], [Tex]\phi(a \cdot b) = \phi(a) \cdot \phi(b)[/Tex] [Tex]\phi(2 \cdot 9) = \phi(2) \cdot \phi(9) = 1 \cdot 6 = 6[/Tex][Tex]\\[/Tex][Tex]\phi(8 \cdot 9) = \phi(8) \cdot \phi(9) = 4 \cdot 6 = 24[/Tex][Tex]\\[/Tex][Tex]\phi(5 \cdot 6) = \phi(5) \cdot \phi(6) = 4 \cdot 2 = 8[/Tex] [Tex]\\[/Tex][Tex]\\[/Tex]Normal Case : [Tex]gcd(a, b) \neq 1[/Tex], [Tex]\phi(a \cdot b) = \phi(a) \cdot \phi(b) \cdot \frac {gcd(a, b)} {\phi(gcd(a, b))}[/Tex][Tex]\\[/Tex][Tex]\phi(4 \cdot 6) = \phi(4) \cdot \phi(6) \cdot \frac {gcd(4, 6)} {\phi(gcd(4, 6))}[/Tex] [Tex]= 2 \cdot 2 \cdot \frac{2}{1}[/Tex] [Tex]= 2 \cdot 2 \cdot 2 = 8[/Tex][Tex]\\[/Tex][Tex]\phi(4 \cdot 8) = \phi(4) \cdot \phi(8) \cdot \frac {gcd(4, 8)} {\phi(gcd(4, 8))} = 2 \cdot 4 \cdot \frac{4}{2} = 2 \cdot 4 \cdot 2 = 16[/Tex][Tex]\\[/Tex][Tex]\phi(6 \cdot 8) = \phi(6) \cdot \phi(8) \cdot \frac {gcd(6, 8)} {\phi(gcd(6, 8))} = 2 \cdot 4 \cdot \frac{2}{1} = 2 \cdot 4 \cdot 2 = 16[/Tex]
5) Sum of values of totient functions of all divisors of n is equal to n.

Examples :
n = 6
factors = {1, 2, 3, 6}
n = [Tex]\phi(1) + \phi(2) + \phi(3) + \phi(6)[/Tex] = 1 + 1 + 2 + 2 = 6[Tex]\\[/Tex]n = 8factors = {1, 2, 4, 8}n = [Tex]\phi(1) + \phi(2) + \phi(4) + \phi(8)[/Tex] = 1 + 1 + 2 + 4 = 8[Tex]\\[/Tex]n = 10factors = {1, 2, 5, 10}n = [Tex]\phi(1) + \phi(2) + \phi(5) + \phi(10)[/Tex] = 1 + 1 + 4 + 4 = 10
6) The most famous and important feature is expressed in Euler’s theorem :
The theorem states that if n and a are coprime
(or relatively prime) positive integers, then
aΦ(n) Φ 1 (mod n)
The RSA cryptosystem is based on this theorem:
In the particular case when m is prime say p, Euler’s theorem turns into the so-called Fermat’s little theorem :
ap-1 Φ 1 (mod p)
7) Number of generators of a finite cyclic group under modulo n addition is Φ(n).
Related Article:
Euler’s Totient function for all numbers smaller than or equal to n
Optimized Euler Totient Function for Multiple Evaluations
References:
http://e-maxx.ru/algo/euler_function
http://en.wikipedia.org/wiki/Euler%27s_totient_function
https://cp-algorithms.com/algebra/phi-function.html
http://mathcenter.oxford.memory.edu/site/math125/chineseRemainderTheorem/
Share your thoughts in the comments
Please Login to comment...