Count number of paths with at-most k turns

Given a “m x n” matrix, count number of paths to reach bottom right from top left with maximum k turns allowed. What is a turn? A movement is considered turn, if we were moving along row and now move along column. OR we were moving along column and now move along row.

There are two possible scenarios when a turn can occur
at point (i, j):

Turns Right: (i-1, j)  ->  (i, j)  ->  (i, j+1)
                      Down        Right

Turns Down:  (i, j-1)  ->  (i, j)  ->  (i+1, j)
                     Right        Down

Examples:

Input:  m = 3, n = 3, k = 2
Output: 4

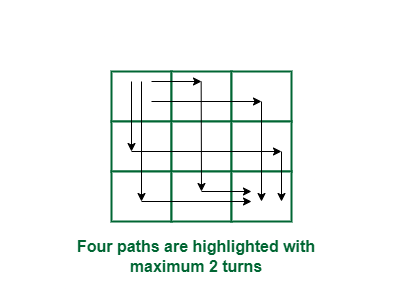
Example: For m = 3, n = 3, k = 2

See below diagram for four paths with 
maximum 2 turns.

Input:  m = 3, n = 3, k = 1
Output: 2 

This problem can be recursively computed using below recursive formula.

countPaths(i, j, k): Count of paths to reach (i,j) from (0, 0)
countPathsDir(i, j, k, 0): Count of paths if we reach (i, j) 
                           along row. 
countPathsDir(i, j, k, 1): Count of paths if we reach (i, j) 
                           along column. 
The fourth parameter in countPathsDir() indicates direction.

Value of countPaths() can be written as:
countPaths(i, j, k) = countPathsDir(i, j, k, 0) + 
                      countPathsDir(i, j, k, 1) 

And value of  countPathsDir() can be recursively defined as:

// Base cases

// If current direction is along row
If (d == 0) 
  // Count paths for two cases
  // 1) We reach here through previous row.
  // 2) We reach here through previous column, so number of 
  //    turns k reduce by 1.
  countPathsDir(i, j, k, d) = countPathsUtil(i, j-1, k, d) +
                              countPathsUtil(i-1, j, k-1, !d);

// If current direction is along column
Else 
  // Similar to above
  countPathsDir(i, j, k, d) =  countPathsUtil(i-1, j, k, d) +
                               countPathsUtil(i, j-1, k-1, !d);

We can solve this problem in Polynomial Time using Dynamic Programming. The idea is to use a 4-dimensional table dp[m][n][k][d] where m is number of rows, n is number of columns, k is number of allowed turns and d is the direction.

Below is the Dynamic Programming-based implementation. 

C++14

// C++ program to count number of paths with maximum
// k turns allowed
#include<bits/stdc++.h>
using namespace std;
#define MAX 100

// table to store results of subproblems
int dp[MAX][MAX][MAX][2];

// Returns count of paths to reach (i, j) from (0, 0)
// using at-most k turns. d is current direction
// d = 0 indicates along row, d = 1 indicates along
// column.
int countPathsUtil(int i, int j, int k, int d)
{
    // If invalid row or column indexes
    if (i < 0 || j < 0)
        return 0;

    // If current cell is top left itself
    if (i == 0 && j == 0)
        return 1;

    // If 0 turns left
    if (k == 0)
    {
        // If direction is row, then we can reach here
        // only if direction is row and row is 0.
        if (d == 0 && i == 0) return 1;

        // If direction is column, then we can reach here
        // only if direction is column and column is 0.
        if (d == 1 && j == 0) return 1;

        return 0;
    }

    // If this subproblem is already evaluated
    if (dp[i][j][k][d] != -1)
        return dp[i][j][k][d];

    // If current direction is row, then count paths for two cases
    // 1) We reach here through previous row.
    // 2) We reach here through previous column, so number of
    //    turns k reduce by 1.
    if (d == 0)
      return dp[i][j][k][d] = countPathsUtil(i, j-1, k, d) +
                              countPathsUtil(i-1, j, k-1, !d);

    // Similar to above if direction is column
    return dp[i][j][k][d] =  countPathsUtil(i-1, j, k, d) +
                             countPathsUtil(i, j-1, k-1, !d);
}

// This function mainly initializes 'dp' array as -1 and calls
// countPathsUtil()
int countPaths(int i, int j, int k)
{
    // If (0, 0) is target itself
    if (i == 0 && j == 0)
          return 1;

    // Initialize 'dp' array
    memset(dp, -1, sizeof dp);

    // Recur for two cases: moving along row and along column
    return countPathsUtil(i-1, j, k, 1) +  // Moving along row
           countPathsUtil(i, j-1, k, 0); // Moving along column
}

// Driver program
int main()
{
    int m = 3, n = 3, k = 2;
    cout << "Number of paths is "
         << countPaths(m-1, n-1, k) << endl;
    return 0;
}

Java

// Java program to count number of paths
// with maximum k turns allowed
import java.util.*;
class GFG
{
static int MAX = 100;

// table to store results of subproblems
static int [][][][]dp = new int[MAX][MAX][MAX][2];

// Returns count of paths to reach (i, j) from (0, 0)
// using at-most k turns. d is current direction
// d = 0 indicates along row, d = 1 indicates along
// column.
static int countPathsUtil(int i, int j, int k, int d)
{
    // If invalid row or column indexes
    if (i < 0 || j < 0)
        return 0;

    // If current cell is top left itself
    if (i == 0 && j == 0)
        return 1;

    // If 0 turns left
    if (k == 0)
    {
        // If direction is row, then we can reach here
        // only if direction is row and row is 0.
        if (d == 0 && i == 0) return 1;

        // If direction is column, then we can reach here
        // only if direction is column and column is 0.
        if (d == 1 && j == 0) return 1;

        return 0;
    }

    // If this subproblem is already evaluated
    if (dp[i][j][k][d] != -1)
        return dp[i][j][k][d];

    // If current direction is row,
    // then count paths for two cases
    // 1) We reach here through previous row.
    // 2) We reach here through previous column,
    // so number of turns k reduce by 1.
    if (d == 0)
    return dp[i][j][k][d] = countPathsUtil(i, j - 1, k, d) +
                            countPathsUtil(i - 1, j, k - 1, d == 1 ? 0 : 1);

    // Similar to above if direction is column
    return dp[i][j][k][d] = countPathsUtil(i - 1, j, k, d) +
                            countPathsUtil(i, j - 1, k - 1, d == 1 ? 0 : 1);
}

// This function mainly initializes 'dp' array
// as -1 and calls countPathsUtil()
static int countPaths(int i, int j, int k)
{
    // If (0, 0) is target itself
    if (i == 0 && j == 0)
        return 1;

    // Initialize 'dp' array
    for(int p = 0; p < MAX; p++)
    {
        for(int q = 0; q < MAX; q++)
        {
            for(int r = 0; r < MAX; r++)
                for(int s = 0; s < 2; s++)
                    dp[p][q][r][s] = -1;
        }
    }

    // Recur for two cases: moving along row and along column
    return countPathsUtil(i - 1, j, k, 1) + // Moving along row
        countPathsUtil(i, j - 1, k, 0); // Moving along column
}

// Driver Code
public static void main(String[] args)
{
    int m = 3, n = 3, k = 2;
    System.out.println("Number of paths is " +
                 countPaths(m - 1, n - 1, k));
}
}

// This code is contributed by Princi Singh

Python3

# Python3 program to count number of paths
# with maximum k turns allowed
MAX = 100

# table to store results of subproblems
dp = [[[[-1 for col in range(2)]
            for col in range(MAX)]
            for row in range(MAX)]
            for row in range(MAX)]

# Returns count of paths to reach
# (i, j) from (0, 0) using at-most k turns.
# d is current direction, d = 0 indicates
# along row, d = 1 indicates along column.
def countPathsUtil(i, j, k, d):

    # If invalid row or column indexes
    if (i < 0 or j < 0):
        return 0

    # If current cell is top left itself
    if (i == 0 and j == 0):
        return 1

    # If 0 turns left
    if (k == 0):

        # If direction is row, then we can reach here
        # only if direction is row and row is 0.
        if (d == 0 and i == 0):
            return 1

        # If direction is column, then we can reach here
        # only if direction is column and column is 0.
        if (d == 1 and j == 0):
            return 1

        return 0

    # If this subproblem is already evaluated
    if (dp[i][j][k][d] != -1):
        return dp[i][j][k][d]

    # If current direction is row,
    # then count paths for two cases
    # 1) We reach here through previous row.
    # 2) We reach here through previous column,
    # so number of turns k reduce by 1.
    if (d == 0):
        dp[i][j][k][d] = countPathsUtil(i, j - 1, k, d) + \
                         countPathsUtil(i - 1, j, k - 1, not d)
        return dp[i][j][k][d]

    # Similar to above if direction is column
    dp[i][j][k][d] = countPathsUtil(i - 1, j, k, d) + \
                     countPathsUtil(i, j - 1, k - 1, not d)
    return dp[i][j][k][d]

# This function mainly initializes 'dp' array
# as -1 and calls countPathsUtil()
def countPaths(i, j, k):

    # If (0, 0) is target itself
    if (i == 0 and j == 0):
        return 1

    # Recur for two cases: moving along row
    # and along column
    return countPathsUtil(i - 1, j, k, 1) +\
           countPathsUtil(i, j - 1, k, 0)

# Driver Code
if __name__ == '__main__':
    m = 3
    n = 3
    k = 2
    print("Number of paths is",
           countPaths(m - 1, n - 1, k))

# This code is contributed by Ashutosh450

C#

// C# program to count number of paths
// with maximum k turns allowed
using System;

class GFG
{
static int MAX = 100;

// table to store to store results of subproblems
static int [,,,]dp = new int[MAX, MAX, MAX, 2];

// Returns count of paths to reach (i, j) from (0, 0)
// using at-most k turns. d is current direction
// d = 0 indicates along row, d = 1 indicates along
// column.
static int countPathsUtil(int i, int j, int k, int d)
{
    // If invalid row or column indexes
    if (i < 0 || j < 0)
        return 0;

    // If current cell is top left itself
    if (i == 0 && j == 0)
        return 1;

    // If 0 turns left
    if (k == 0)
    {
        // If direction is row, then we can reach here
        // only if direction is row and row is 0.
        if (d == 0 && i == 0) return 1;

        // If direction is column, then we can reach here
        // only if direction is column and column is 0.
        if (d == 1 && j == 0) return 1;

        return 0;
    }

    // If this subproblem is already evaluated
    if (dp[i, j, k, d] != -1)
        return dp[i, j, k, d];

    // If current direction is row,
    // then count paths for two cases
    // 1) We reach here through previous row.
    // 2) We reach here through previous column,
    // so number of turns k reduce by 1.
    if (d == 0)
    return dp[i, j, k, d] = countPathsUtil(i, j - 1, k, d) +
                            countPathsUtil(i - 1, j, k - 1,
                                            d == 1 ? 0 : 1);

    // Similar to above if direction is column
    return dp[i, j, k, d] = countPathsUtil(i - 1, j, k, d) +
                            countPathsUtil(i, j - 1, k - 1,
                                            d == 1 ? 0 : 1);
}

// This function mainly initializes 'dp' array
// as -1 and calls countPathsUtil()
static int countPaths(int i, int j, int k)
{
    // If (0, 0) is target itself
    if (i == 0 && j == 0)
        return 1;

    // Initialize 'dp' array
    for(int p = 0; p < MAX; p++)
    {
        for(int q = 0; q < MAX; q++)
        {
            for(int r = 0; r < MAX; r++)
                for(int s = 0; s < 2; s++)
                    dp[p, q, r, s] = -1;
        }
    }

    // Recur for two cases: moving along row and along column
    return countPathsUtil(i - 1, j, k, 1) + // Moving along row
           countPathsUtil(i, j - 1, k, 0); // Moving along column
}

// Driver Code
public static void Main(String[] args)
{
    int m = 3, n = 3, k = 2;
    Console.WriteLine("Number of paths is " +
                countPaths(m - 1, n - 1, k));
}
}

// This code is contributed by PrinciRaj1992

Javascript

<script>

// JavaScript program to count number of paths
// with maximum k turns allowed
const MAX = 100

// table to store results of subproblems
let dp = new Array(MAX)
for(let i = 0; i < MAX; i++){
   dp[i] = new Array(MAX)
   for(let j = 0; j < MAX; j++){
      dp[i][j] = new Array(MAX)
      for(let k = 0; k < MAX; k++){
         dp[i][j][k] = new Array(2).fill(-1)
      }
   }
}

// Returns count of paths to reach
// (i, j) from (0, 0) using at-most k turns.
// d is current direction, d = 0 indicates
// along row, d = 1 indicates along column.
function countPathsUtil(i, j, k, d){

    // If invalid row or column indexes
    if (i < 0 || j < 0)
        return 0

    // If current cell is top left itself
    if (i == 0 && j == 0)
        return 1

    // If 0 turns left
    if (k == 0){

        // If direction is row, then we can reach here
        // only if direction is row && row is 0.
        if (d == 0 && i == 0)
            return 1

        // If direction is column, then we can reach here
        // only if direction is column && column is 0.
        if (d == 1 && j == 0)
            return 1

        return 0
   }

    // If this subproblem is already evaluated
    if (dp[i][j][k][d] != -1)
        return dp[i][j][k][d]

    // If current direction is row,
    // then count paths for two cases
    // 1) We reach here through previous row.
    // 2) We reach here through previous column,
    // so number of turns k reduce by 1.
    if (d == 0){
        dp[i][j][k][d] = countPathsUtil(i, j - 1, k, d) +
                        countPathsUtil(i - 1, j, k - 1, d^1)
        return dp[i][j][k][d]
   }

    // Similar to above if direction is column
    dp[i][j][k][d] = countPathsUtil(i - 1, j, k, d) +
                    countPathsUtil(i, j - 1, k - 1, d^1)
    return dp[i][j][k][d]
}

// This function mainly initializes 'dp' array
// as -1 && calls countPathsUtil()
function countPaths(i, j, k){

    // If (0, 0) is target itself
    if (i == 0 && j == 0)
        return 1

    // Recur for two cases: moving along row
    // && along column
    return countPathsUtil(i - 1, j, k, 1) +
        countPathsUtil(i, j - 1, k, 0)
}

// Driver Code
let m = 3
let n = 3
let k = 2
document.write("Number of paths is",
        countPaths(m - 1, n - 1, k))

// This code is contributed by shinjanpatra

</script>

Output

Number of paths is 4

Time Complexity: O(m*n*k)
Auxiliary Space: O(MAX³)

Thanks to Gaurav Ahirwar for suggesting this solution. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.