Convert given Binary Tree to Doubly Linked List in Linear time
Last Updated :
10 Jan, 2023
Given a Binary Tree (BT), convert it to a Doubly Linked List(DLL) In-Place. The left and right pointers in nodes are to be used as previous and next pointers respectively in converted DLL. The order of nodes in DLL must be same as Inorder of the given Binary Tree. The first node of Inorder traversal (left most node in BT) must be head node of the DLL.
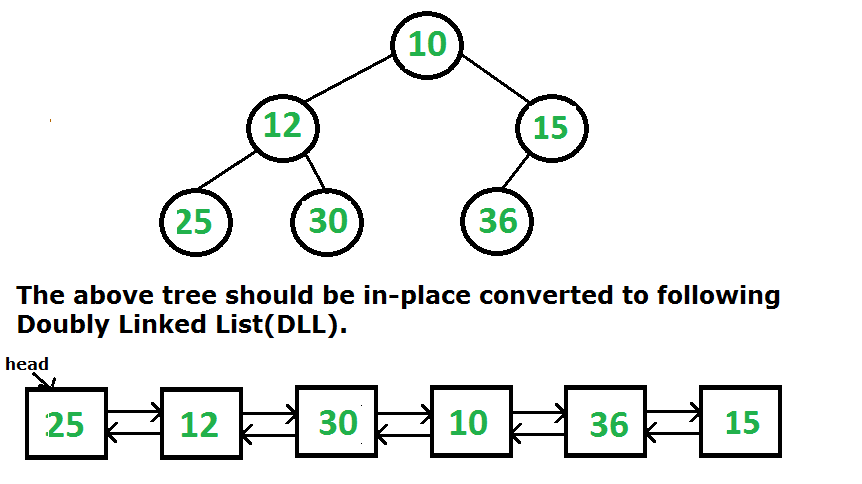
Below three different solutions have been discussed for this problem.
Convert a given Binary Tree to Doubly Linked List | Set 1
Convert a given Binary Tree to Doubly Linked List | Set 2
Convert a given Binary Tree to Doubly Linked List | Set 3
In the following implementation, we traverse the tree in inorder fashion. We add nodes at the beginning of current linked list and update head of the list using pointer to head pointer. Since we insert at the beginning, we need to process leaves in reverse order. For reverse order, we first traverse the right subtree before the left subtree. i.e. do a reverse inorder traversal.
C++
#include <bits/stdc++.h>
struct Node {
int data;
Node *left, *right;
};
Node* newNode(int data)
{
Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return node;
}
void BToDLL(Node* root, Node*& head)
{
if (root == NULL)
return;
BToDLL(root->right, head);
root->right = head;
if (head != NULL)
head->left = root;
head = root;
BToDLL(root->left, head);
}
void printList(Node* head)
{
printf("Extracted Double Linked list is:\n");
while (head) {
printf("%d ", head->data);
head = head->right;
}
}
int main()
{
Node* root = newNode(5);
root->left = newNode(3);
root->right = newNode(6);
root->left->left = newNode(1);
root->left->right = newNode(4);
root->right->right = newNode(8);
root->left->left->left = newNode(0);
root->left->left->right = newNode(2);
root->right->right->left = newNode(7);
root->right->right->right = newNode(9);
Node* head = NULL;
BToDLL(root, head);
printList(head);
return 0;
}
|
Java
class Node {
int data;
Node left, right;
public Node(int data)
{
this.data = data;
left = right = null;
}
}
class BinaryTree {
Node root;
Node head;
void BToDLL(Node root)
{
if (root == null)
return;
BToDLL(root.right);
root.right = head;
if (head != null)
head.left = root;
head = root;
BToDLL(root.left);
}
void printList(Node head)
{
System.out.println("Extracted Double Linked List is : ");
while (head != null) {
System.out.print(head.data + " ");
head = head.right;
}
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(5);
tree.root.left = new Node(3);
tree.root.right = new Node(6);
tree.root.left.right = new Node(4);
tree.root.left.left = new Node(1);
tree.root.right.right = new Node(8);
tree.root.left.left.right = new Node(2);
tree.root.left.left.left = new Node(0);
tree.root.right.right.left = new Node(7);
tree.root.right.right.right = new Node(9);
tree.BToDLL(tree.root);
tree.printList(tree.head);
}
}
|
Python3
class Node:
def __init__(self, data):
self.data = data
self.left = self.right = None
class BinaryTree:
root, head = None, None
def BToDll(self, root: Node):
if root is None:
return
self.BToDll(root.right)
root.right = self.head
if self.head is not None:
self.head.left = root
self.head = root
self.BToDll(root.left)
@staticmethod
def print_list(head: Node):
print('Extracted Double Linked list is:')
while head is not None:
print(head.data, end = ' ')
head = head.right
if __name__ == '__main__':
tree = BinaryTree()
tree.root = Node(5)
tree.root.left = Node(3)
tree.root.right = Node(6)
tree.root.left.left = Node(1)
tree.root.left.right = Node(4)
tree.root.right.right = Node(8)
tree.root.left.left.left = Node(0)
tree.root.left.left.right = Node(2)
tree.root.right.right.left = Node(7)
tree.root.right.right.right = Node(9)
tree.BToDll(tree.root)
tree.print_list(tree.head)
|
C#
using System;
public class Node {
public int data;
public Node left, right;
public Node(int data)
{
this.data = data;
left = right = null;
}
}
class GFG {
public Node root;
public Node head;
public virtual void BToDLL(Node root)
{
if (root == null)
return;
BToDLL(root.right);
root.right = head;
if (head != null)
head.left = root;
head = root;
BToDLL(root.left);
}
public virtual void printList(Node head)
{
Console.WriteLine("Extracted Double "
+ "Linked List is : ");
while (head != null) {
Console.Write(head.data + " ");
head = head.right;
}
}
public static void Main(string[] args)
{
GFG tree = new GFG();
tree.root = new Node(5);
tree.root.left = new Node(3);
tree.root.right = new Node(6);
tree.root.left.right = new Node(4);
tree.root.left.left = new Node(1);
tree.root.right.right = new Node(8);
tree.root.left.left.right = new Node(2);
tree.root.left.left.left = new Node(0);
tree.root.right.right.left = new Node(7);
tree.root.right.right.right = new Node(9);
tree.BToDLL(tree.root);
tree.printList(tree.head);
}
}
|
Javascript
<script>
class Node {
constructor(data)
{
this.data = data;
this.left = this.right = null;
}
}
var root;
var head;
function BToDLL( root)
{
if (root == null)
return;
BToDLL(root.right);
root.right = head;
if (head != null)
head.left = root;
head = root;
BToDLL(root.left);
}
function printList( head)
{
document.write("Extracted Double Linked List is :<br/> ");
while (head != null) {
document.write(head.data + " ");
head = head.right;
}
}
root = new Node(5);
root.left = new Node(3);
root.right = new Node(6);
root.left.right = new Node(4);
root.left.left = new Node(1);
root.right.right = new Node(8);
root.left.left.right = new Node(2);
root.left.left.left = new Node(0);
root.right.right.left = new Node(7);
root.right.right.right = new Node(9);
BToDLL(root);
printList(head);
</script>
|
Output
Extracted Double Linked list is:
0 1 2 3 4 5 6 7 8 9
Time Complexity: O(n), as the solution does a single traversal of given Binary Tree.
Auxiliary Space: O(n)
Share your thoughts in the comments
Please Login to comment...