M-Coloring Problem
Last Updated :
10 Oct, 2023
Given an undirected graph and a number m, the task is to color the given graph with at most m colors such that no two adjacent vertices of the graph are colored with the same color
Note: Here coloring of a graph means the assignment of colors to all vertices
Below is an example of a graph that can be colored with 3 different colors:
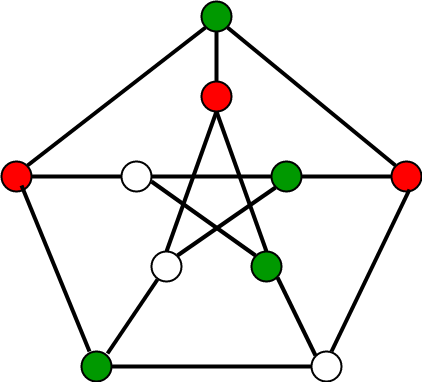
Examples:
Input: graph = {0, 1, 1, 1},
{1, 0, 1, 0},
{1, 1, 0, 1},
{1, 0, 1, 0}
Output: Solution Exists: Following are the assigned colors: 1 2 3 2
Explanation: By coloring the vertices with following colors,
adjacent vertices does not have same colors
Input: graph = {1, 1, 1, 1},
{1, 1, 1, 1},
{1, 1, 1, 1},
{1, 1, 1, 1}
Output: Solution does not exist
Explanation: No solution exits
Naive Approach for M-Coloring Problem:
Generate all possible configurations of colors. Since each node can be colored using any of the m available colors, the total number of color configurations possible is mV. After generating a configuration of color, check if the adjacent vertices have the same color or not. If the conditions are met, print the combination.
Time Complexity: O(mV). There is a total O(mV) combination of colors
Auxiliary Space: O(V). The Recursive Stack of graph coloring(…) function will require O(V) space.
M-Coloring Problem using Backtracking:
Assign colors one by one to different vertices, starting from vertex 0. Before assigning a color, check for safety by considering already assigned colors to the adjacent vertices i.e check if the adjacent vertices have the same color or not. If there is any color assignment that does not violate the conditions, mark the color assignment as part of the solution. If no assignment of color is possible then backtrack and return false
Follow the given steps to solve the problem:
- Create a recursive function that takes the graph, current index, number of vertices, and color array.
- If the current index is equal to the number of vertices. Print the color configuration in the color array.
- Assign a color to a vertex from the range (1 to m).
- For every assigned color, check if the configuration is safe, (i.e. check if the adjacent vertices do not have the same color) and recursively call the function with the next index and number of vertices otherwise, return false
- If any recursive function returns true then return true
- If no recursive function returns true then return false
Illustration:
- To color the graph, color each node one by one.
- To color the first node there are 3 choices of colors Red, Green and Blue, so lets take the red color for first node.
- After Red color for first node is fixed then we have made choice for second node in similar manner as we did for first node, then for 3rd node and so on.
- There is one important point to remember. while choosing color for the node, it should not be same as the color of the adjacent node.

Choosing Red For Node 1
- As shown in the above diagram, all the solutions are shown by coloring the first node in Red.
- Let’s choose Green color for the first node and explore the options for the remaining nodes.

Choosing Green for Node 1
- As shown in the above diagram, all the solutions are shown by coloring the first node in Green.
- Let’s choose Blue color for the first node and explore the options for the remaining nodes.
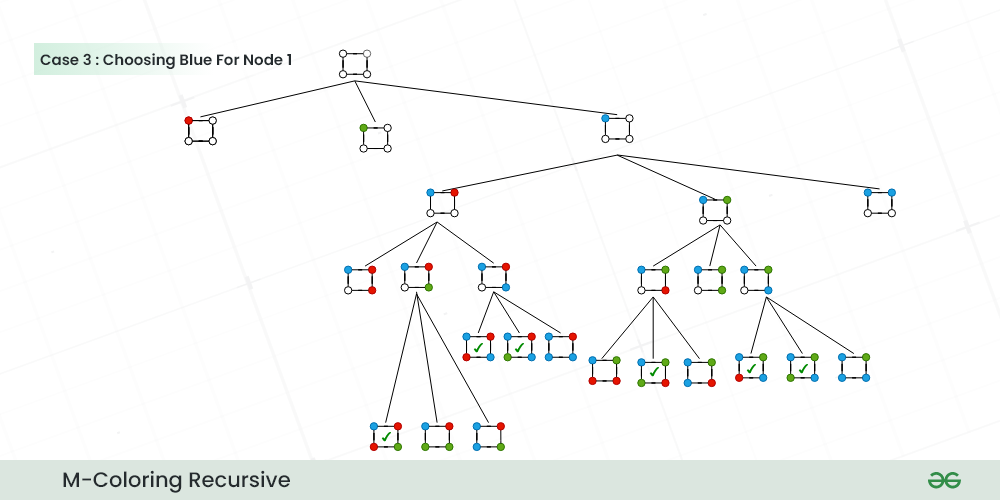
Choosing Blue for Node 1
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define V 4
void printSolution(int color[]);
bool isSafe(int v, bool graph[V][V], int color[], int c)
{
for (int i = 0; i < V; i++)
if (graph[v][i] && c == color[i])
return false;
return true;
}
bool graphColoringUtil(bool graph[V][V], int m, int color[],
int v)
{
if (v == V)
return true;
for (int c = 1; c <= m; c++) {
if (isSafe(v, graph, color, c)) {
color[v] = c;
if (graphColoringUtil(graph, m, color, v + 1)
== true)
return true;
color[v] = 0;
}
}
return false;
}
bool graphColoring(bool graph[V][V], int m)
{
int color[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (graphColoringUtil(graph, m, color, 0) == false) {
cout << "Solution does not exist";
return false;
}
printSolution(color);
return true;
}
void printSolution(int color[])
{
cout << "Solution Exists:"
<< " Following are the assigned colors"
<< "\n";
for (int i = 0; i < V; i++)
cout << " " << color[i] << " ";
cout << "\n";
}
int main()
{
bool graph[V][V] = {
{ 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 },
};
int m = 3;
graphColoring(graph, m);
return 0;
}
|
C
#include <stdbool.h>
#include <stdio.h>
#define V 4
void printSolution(int color[]);
bool isSafe(int v, bool graph[V][V], int color[], int c)
{
for (int i = 0; i < V; i++)
if (graph[v][i] && c == color[i])
return false;
return true;
}
bool graphColoringUtil(bool graph[V][V], int m, int color[],
int v)
{
if (v == V)
return true;
for (int c = 1; c <= m; c++) {
if (isSafe(v, graph, color, c)) {
color[v] = c;
if (graphColoringUtil(graph, m, color, v + 1)
== true)
return true;
color[v] = 0;
}
}
return false;
}
bool graphColoring(bool graph[V][V], int m)
{
int color[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (graphColoringUtil(graph, m, color, 0) == false) {
printf("Solution does not exist");
return false;
}
printSolution(color);
return true;
}
void printSolution(int color[])
{
printf("Solution Exists:"
" Following are the assigned colors \n");
for (int i = 0; i < V; i++)
printf(" %d ", color[i]);
printf("\n");
}
int main()
{
bool graph[V][V] = {
{ 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 },
};
int m = 3;
graphColoring(graph, m);
return 0;
}
|
Java
public class mColoringProblem {
final int V = 4;
int color[];
boolean isSafe(int v, int graph[][], int color[], int c)
{
for (int i = 0; i < V; i++)
if (graph[v][i] == 1 && c == color[i])
return false;
return true;
}
boolean graphColoringUtil(int graph[][], int m,
int color[], int v)
{
if (v == V)
return true;
for (int c = 1; c <= m; c++) {
if (isSafe(v, graph, color, c)) {
color[v] = c;
if (graphColoringUtil(graph, m, color,
v + 1))
return true;
color[v] = 0;
}
}
return false;
}
boolean graphColoring(int graph[][], int m)
{
color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (!graphColoringUtil(graph, m, color, 0)) {
System.out.println("Solution does not exist");
return false;
}
printSolution(color);
return true;
}
void printSolution(int color[])
{
System.out.println("Solution Exists: Following"
+ " are the assigned colors");
for (int i = 0; i < V; i++)
System.out.print(" " + color[i] + " ");
System.out.println();
}
public static void main(String args[])
{
mColoringProblem Coloring = new mColoringProblem();
int graph[][] = {
{ 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 },
};
int m = 3;
Coloring.graphColoring(graph, m);
}
}
|
Python3
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
def isSafe(self, v, colour, c):
for i in range(self.V):
if self.graph[v][i] == 1 and colour[i] == c:
return False
return True
def graphColourUtil(self, m, colour, v):
if v == self.V:
return True
for c in range(1, m + 1):
if self.isSafe(v, colour, c) == True:
colour[v] = c
if self.graphColourUtil(m, colour, v + 1) == True:
return True
colour[v] = 0
def graphColouring(self, m):
colour = [0] * self.V
if self.graphColourUtil(m, colour, 0) == None:
return False
print("Solution exist and Following are the assigned colours:")
for c in colour:
print(c, end=' ')
return True
if __name__ == '__main__':
g = Graph(4)
g.graph = [[0, 1, 1, 1], [1, 0, 1, 0], [1, 1, 0, 1], [1, 0, 1, 0]]
m = 3
g.graphColouring(m)
|
C#
using System;
class GFG {
readonly int V = 4;
int[] color;
bool isSafe(int v, int[, ] graph, int[] color, int c)
{
for (int i = 0; i < V; i++)
if (graph[v, i] == 1 && c == color[i])
return false;
return true;
}
bool graphColoringUtil(int[, ] graph, int m,
int[] color, int v)
{
if (v == V)
return true;
for (int c = 1; c <= m; c++) {
if (isSafe(v, graph, color, c)) {
color[v] = c;
if (graphColoringUtil(graph, m, color,
v + 1))
return true;
color[v] = 0;
}
}
return false;
}
bool graphColoring(int[, ] graph, int m)
{
color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (!graphColoringUtil(graph, m, color, 0)) {
Console.WriteLine("Solution does not exist");
return false;
}
printSolution(color);
return true;
}
void printSolution(int[] color)
{
Console.WriteLine("Solution Exists: Following"
+ " are the assigned colors");
for (int i = 0; i < V; i++)
Console.Write(" " + color[i] + " ");
Console.WriteLine();
}
public static void Main(String[] args)
{
GFG Coloring = new GFG();
int[, ] graph = { { 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 } };
int m = 3;
Coloring.graphColoring(graph, m);
}
}
|
Javascript
<script>
let V = 4;
let color;
function isSafe(v,graph,color,c)
{
for (let i = 0; i < V; i++)
if (
graph[v][i] == 1 && c == color[i])
return false;
return true;
}
function graphColoringUtil(graph,m,color,v)
{
if (v == V)
return true;
for (let c = 1; c <= m; c++)
{
if (isSafe(v, graph, color, c))
{
color[v] = c;
if (
graphColoringUtil(
graph, m,
color, v + 1))
return true;
color[v] = 0;
}
}
return false;
}
function graphColoring(graph,m)
{
color = new Array(V);
for (let i = 0; i < V; i++)
color[i] = 0;
if (
!graphColoringUtil(
graph, m, color, 0))
{
document.write(
"Solution does not exist<br>");
return false;
}
printSolution(color);
return true;
}
function printSolution(color)
{
document.write(
"Solution Exists: Following"
+ " are the assigned colors<br>");
for (let i = 0; i < V; i++)
document.write(" " + color[i] + " ");
document.write("<br>");
}
let graph = [
[ 0, 1, 1, 1 ],
[ 1, 0, 1, 0 ],
[ 1, 1, 0, 1 ],
[ 1, 0, 1, 0 ],
];
let m = 3;
graphColoring(graph, m);
</script>
|
Output
Solution Exists: Following are the assigned colors
1 2 3 2
Time Complexity: O(mV). There is a total of O(mV) combinations of colors. The upper bound time complexity remains the same but the average time taken will be less.
Auxiliary Space: O(V). The recursive Stack of the graph coloring function will require O(V) space.
Share your thoughts in the comments
Please Login to comment...