What is the distance between two parallel lines?

Mensuration comes from the Latin word mensurate which means ‘to measure’. So mensuration chapter is all about measuring various values. In mathematics, calculations, and measurement of different values are required, hence, mensuration is studied. Let’s try to measure the distance between two parallel lines. 

Parallel lines

Any lines that have the same slope are called parallel lines, or they can be thought of as two or more lines that intersect each other at infinity. This means that they will never ever intersect even if the line is extending towards infinity. Properties of parallel lines when a transverse intersects two parallel lines at an angle θ:

Considering the figure the properties are defined as follows:

• ∠a = ∠b and they are called corresponding angles
• ∠c = ∠a and they are called vertically opposite angles
• ∠c + ∠b = 180°
• ∠c = ∠d and they are called alternate interior angles.

Slope

The slope is defined as the rate of change of ordinate (y-coordinate) with respect to the abscissa (x-coordinate). It is denoted by the letter m. It basically tells by what factor the y-coordinate will change if x changes from x to x+a where a, is a real number. The formula to calculate the slope of any given line is:

slope =  y₂ – y₁/x₂ – x₁

The slope (m) can also be expressed as a trigonometric function., in terms of θ the angle made by the line with the x-axis. Slope m = tan θ = (y₂ – y₁)/(x₂ – x₁) 

What is the distance between two parallel lines?

Solution:

To measure the distance between two parallel lines. Let’s take two arbitrary parallel lines. Two parallel lines will have the same slope. The equation of a line is y = mx + c. So the equations of the two lines will be somewhat like this:

y = mx + c₁

y = mx + c₂

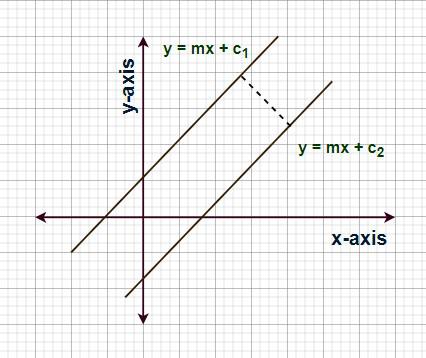
As shown in the above figure, the two lines are drawn with a slope equal to m. The distance between them has been taken as d.  The line y = mx + c₁ intercepts the y-axis at the point A(0, c₁) and the other line y = mx + c₂ intercepts the y-axis at B(0, c₂). The length AB is given by c₂ – c₁,  d can be calculated using trigonometry considering the triangle ABC. Considering the triangle ABC,  

d = AB × cos θ

Or, d = (c₂ – c₁) × cos θ

Or, d = (c₂ – c₁)/ (sec θ); since, cos θ = 1/sec θ

Or, d = (c₂ – c₁) / √(1 + tan² θ) ;  since, sec² θ = 1 + tan² θ

Or d = (c₂ – c₁)/√(1 + m²)

Therefore, the distance d between two parallel lines is given by,

Sample Questions

Question 1: Check whether the lines 5y = 45x +15 and y = 9x + 3 are parallel or not.

Solution:  

Given the equation of lines are,

Equation 1: 5y = 45x + 15

Equation 2: y = 9x + 3

In order to check if these two lines are parallel or not, compare their slope and check if its equal.

Equation 1: 5y = 45x + 9

Taking 5 common in R.H.S 

5y = 5(9x + 3)

Or, y = 9x + 3

As, equation 1 and equation 2 are the same equation after evaluating and their slopes are same. So the given lines are parallel lines.

Question 2: Find the distance between the lines y = 2x + 5 and y = 2x + 10

Solution:

m = slope = 2

c₁ = 5

c₂ = 10

Let the distance between the two lines is d

Using the formula we get,

|10 – 5|

d = √(1+2²)

d = √5 units

Question 3:  Find the distance between the lines y = 2x + 5 and 5y = 10x + 20

Solution:

Equation of second line can be written as 5 × y = 5 × (2x + 4)

Or, y = 2x + 4

Therefore m = slope = 2

c₁ = 5

c₂ = 4

Let the distance between the two lines is d

Using the formula,

|5 – 4|

d = √(1 + 2²)

d = 1/√5 = 0.022 units

My Personal Notes arrow_drop_up

Save