Van Emde Boas Tree | Set 1 | Basics and Construction
Last Updated :
04 Dec, 2023
It is highly recommended to fully understand Proto Van Emde Boas Tree. Van Emde Boas Tree supports search, successor, predecessor, insert and delete operations in O(lglgN) time which is faster than any of related data structures like priority queue, binary search tree, etc. Van Emde Boas Tree works with O(1) time-complexity for minimum and maximum query. Here N is the size of the universe over which tree is defined and lg is log base 2. Note: Van Emde Boas Data Structure’s key set must be defined over a range of 0 to n(n is positive integer of the form 2k) and it works when duplicate keys are not allowed. Abbreviations:
- VEB is an abbreviation of Van Emde Boas tree.
- VEB(
 ) is an abbreviation for VEB containing u number of keys.
) is an abbreviation for VEB containing u number of keys.
Structure of Van Emde Boas Tree:  Van Emde Boas Tree is a recursively defined structure.
Van Emde Boas Tree is a recursively defined structure.
- u: Number of keys present in the VEB Tree.
- Minimum: Contains the minimum key present in the VEB Tree.
- Maximum: Contains the maximum key present in the VEB Tree.
- Summary: Points to new VEB(
 ) Tree which contains overview of keys present in clusters array.
) Tree which contains overview of keys present in clusters array. - Clusters: An array of size
 each place in the array points to new VEB(
each place in the array points to new VEB( ) Tree.
) Tree.
See the image below to understand the basics of Van Emde Boas Tree, although it does not represent the actual structure of Van Emde Boas Tree:  Basic Understanding of Van Emde Boas Tree:
Basic Understanding of Van Emde Boas Tree:
- Van Emde Boas Tree is recursively defined structure similar to Proto Van Emde Boas Tree.
- In Van Emde Boas Tree, Minimum and Maximum queries works in O(1) time as Van Emde Boas Tree stores Minimum and Maximum keys present in the tree structure.
- Advantages of adding Maximum and Minimum attributes, which help to decrease time complexity:
- If any of Minimum and Maximum value of VEB Tree is empty(NIL or -1 in code) then there is no element present in the Tree.
- If both Minimum and Maximum is equal then only one value is present in the structure.
- If both are present and distinct then two or more elements are present in the Tree.
- We can insert and delete keys by just setting maximum and minimum values as per conditions in constant time( O(1) ) which helps in decreasing recursive call chain: If only one key is present in the VEB then to delete that key we simply set min and max to the nil value. Similarly, if no keys are present then we can insert by just setting min and max to the key we want to insert. These are O(1) operations.
- In successor and predecessor queries, we can take decisions from minimum and maximum values of VEB, which will make our work easier.
In Proto Van Emde Boas Tree the size of universe size is restricted to be of type 22k but in Van Emde Boas Tree, it allows the universe size to be exact power of two. So we need to modify High(x), low(x), generate_index() helper functions used in Proto Van Emde Boas Tree as below.
- High(x): It will return floor( x/ceil(
 ) ), which is basically the cluster index in which the key x is present.
) ), which is basically the cluster index in which the key x is present.
High(x) = floor(x/ceil(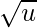 ))
))
- Low(x): It will return x mod ceil(
 ) which is its position in the cluster.
) which is its position in the cluster.
Low(x) = x % ceil( 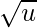 )
)
- generate_index(a, b) : It will return position of key from its position in cluster b and its cluster index a.
generate_index(a, b) = a * ceil(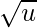 ) + b
) + b
Construction of Van Emde Boas Tree: Construction of Van Emde Boas Tree is very similar to Proto Van Emde Boas Tree. Difference here is that we are allowing the universe size to be any power of two, so that high(), low(), generate_index() will be different.
To construct, empty VEB: The procedure is the same as Proto VEB just two things minimum and maximum will be added in each VEB. To represent that minimum and maximum is null we will represent it as -1.
Note: In the base case, we just need minimum and maximum values because adding a cluster of size 2 will be redundant after the addition of min and max values.
Below is the implementation:
C++
#include <bits/stdc++.h>
using namespace std;
class Van_Emde_Boas {
public:
int universe_size;
int minimum;
int maximum;
Van_Emde_Boas* summary;
vector<Van_Emde_Boas*> clusters;
int high(int x)
{
int div = ceil(sqrt(universe_size));
return x / div;
}
int low(int x)
{
int mod = ceil(sqrt(universe_size));
return x % mod;
}
int generate_index(int x, int y)
{
int ru = ceil(sqrt(universe_size));
return x * ru + y;
}
Van_Emde_Boas(int size)
{
universe_size = size;
minimum = -1;
maximum = -1;
if (size <= 2) {
summary = nullptr;
clusters = vector<Van_Emde_Boas*>(0, nullptr);
}
else {
int no_clusters = ceil(sqrt(size));
summary = new Van_Emde_Boas(no_clusters);
clusters = vector<Van_Emde_Boas*>(no_clusters, nullptr);
for (int i = 0; i < no_clusters; i++) {
clusters[i] = new Van_Emde_Boas(ceil(sqrt(size)));
}
}
}
};
int main()
{
Van_Emde_Boas* akp = new Van_Emde_Boas(4);
}
|
Java
class VanEmdeBoas {
int universeSize;
int minimum;
int maximum;
VanEmdeBoas summary;
VanEmdeBoas[] clusters;
public VanEmdeBoas(int size) {
this.universeSize = size;
this.minimum = -1;
this.maximum = -1;
if (size <= 2) {
this.summary = null;
this.clusters = new VanEmdeBoas[0];
} else {
int noClusters = (size + 1) / 2;
this.summary = new VanEmdeBoas(noClusters);
this.clusters = new VanEmdeBoas[noClusters];
for (int i = 0; i < noClusters; i++) {
this.clusters[i] = new VanEmdeBoas((size + 1) / 2);
}
}
}
int high(int x) {
int div = (this.universeSize + 1) / 2;
return x / div;
}
int low(int x) {
int mod = (this.universeSize + 1) / 2;
return x % mod;
}
int generateIndex(int x, int y) {
int ru = (this.universeSize + 1) / 2;
return x * ru + y;
}
public static void main(String[] args) {
VanEmdeBoas akp = new VanEmdeBoas(16);
}
}
|
Python3
class Van_Emde_Boas:
def __init__(self, size):
self.universe_size = size
self.minimum = -1
self.maximum = -1
if size <= 2:
self.summary = None
self.clusters = [None] * 0
else:
no_clusters = (size + 1) // 2
self.summary = Van_Emde_Boas(no_clusters)
self.clusters = [None] * no_clusters
for i in range(no_clusters):
self.clusters[i] = Van_Emde_Boas((size + 1) // 2)
def high(self, x):
div = (self.universe_size + 1) // 2
return x // div
def low(self, x):
mod = (self.universe_size + 1) // 2
return x % mod
def generate_index(self, x, y):
ru = (self.universe_size + 1) // 2
return x * ru + y
if __name__ == '__main__':
akp = Van_Emde_Boas(16)
|
C#
using System;
public class VanEmdeBoas
{
public int universeSize;
public int minimum;
public int maximum;
public VanEmdeBoas summary;
public VanEmdeBoas[] clusters;
public VanEmdeBoas SetSummary(VanEmdeBoas summary)
{
this.summary = summary;
return this.summary;
}
public VanEmdeBoas(int size)
{
this.universeSize = size;
this.minimum = -1;
this.maximum = -1;
if (size <= 2)
{
this.summary = null;
this.clusters = new VanEmdeBoas[0];
}
else
{
int noClusters = (size + 1) / 2;
this.summary = new VanEmdeBoas(noClusters);
this.clusters = new VanEmdeBoas[noClusters];
for (int i = 0; i < noClusters; i++)
{
this.clusters[i] = new VanEmdeBoas((size + 1) / 2);
}
}
}
int High(int x)
{
int div = (this.universeSize + 1) / 2;
return x / div;
}
int Low(int x)
{
int mod = (this.universeSize + 1) / 2;
return x % mod;
}
int GenerateIndex(int x, int y)
{
int ru = (this.universeSize + 1) / 2;
return x * ru + y;
}
public static void Main(string[] args)
{
VanEmdeBoas akp = new VanEmdeBoas(16);
akp.SetSummary(akp);
}
}
|
Javascript
class VanEmdeBoas {
constructor(size) {
this.universeSize = size;
this.minimum = -1;
this.maximum = -1;
if (size <= 2) {
this.summary = null;
this.clusters = [];
} else {
const noClusters = Math.ceil(Math.sqrt(size));
this.summary = new VanEmdeBoas(noClusters);
this.clusters = Array.from({ length: noClusters }, () => new VanEmdeBoas(Math.ceil(Math.sqrt(size))));
for (let i = 0; i < noClusters; i++) {
this.clusters[i] = new VanEmdeBoas(Math.ceil(Math.sqrt(size)));
}
}
}
high(x) {
const div = Math.ceil(Math.sqrt(this.universeSize));
return Math.floor(x / div);
}
low(x) {
const mod = Math.ceil(Math.sqrt(this.universeSize));
return x % mod;
}
generateIndex(x, y) {
const ru = Math.ceil(Math.sqrt(this.universeSize));
return x * ru + y;
}
}
const akp = new VanEmdeBoas(16);
|
Share your thoughts in the comments
Please Login to comment...