proto van Emde Boas Trees | Set 1 (Background and Introduction)
Last Updated :
13 Jun, 2023
Let us consider the below problem statement and think of different solutions for it. Given a set S of elements such that the elements are taken from universe {0, 1, …. u-1}, perform following operations efficiently.
- insert(x) : Adds an item x to the set+ S.
- isEmpty() : Returns true if S is empty, else false.
- find(x) : Returns true if x is present in S, else false.
- insert(x) : Inserts an item x to S.
- delete(x) : Delete an item x from S.
- max() : Returns maximum value from S.
- min() : Returns minimum value from S.
- successor(x) : Returns the smallest value in S which is greater than x.
- predecessor(x) : Returns the largest value in S which is smaller than x.
Different Solutions Below are different solutions for the above problem.
- One solution to solve above problem is to use a self-balancing Binary Search Tree like Red-Black Tree, AVL Tree, etc. With this solution, we can perform all above operations in O(Log n) time.
- Another solution is to use Binary Array (or Bitvector). We create an array of size u and mark presence and absence of an element as 1 or 0 respectively. This solution supports insert(), delete() and find() in O(1) time, but other operations may take O(u) time in worst case.
- Van Emde Boas tree (or vEB tree) supports insert(), delete, find(), successor() and predecessor() operations in O(Log Log u) time, and max() and min() in O(1) time. Note : In BST solution, we have time complexity in terms of n, here we have time complexity in terms of u. So Van Emde Boas tree may not be suitable when u is much larger than n.
Background (Superimposing a Binary Tree Structure on Binary Array solution) The time complexities of max(), min(), successor() and predecessor() are high in case of Binary Array solution. The idea is to reduce time complexities of these operations by superimposing a binary tree structure over it. 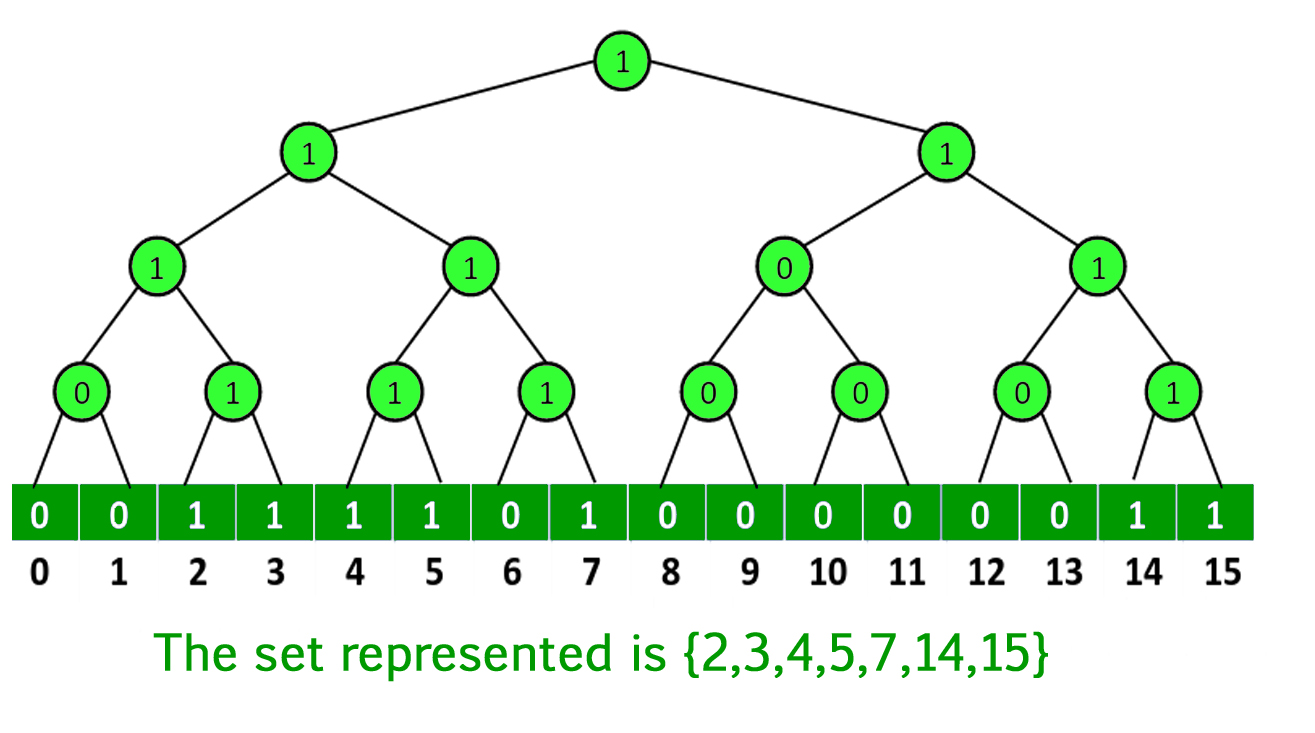
Explanation of above structure:
- Leaves of binary tree represent entries of binary array.
- An internal node has value 1 if any of its children has value 1, i.e., value of an internal node is bitwise OR of all values of its children.
With above structure, we have optimized max(), min(), successor() and predecessor() to time complexity O(Log u).
- min() : Start with root and traverse to a leaf using following rules. While traversing, always choose the leftmost child, i.e., see if left child is 1, go to left child, else go to right child. The leaf node we reach this way is minimum.
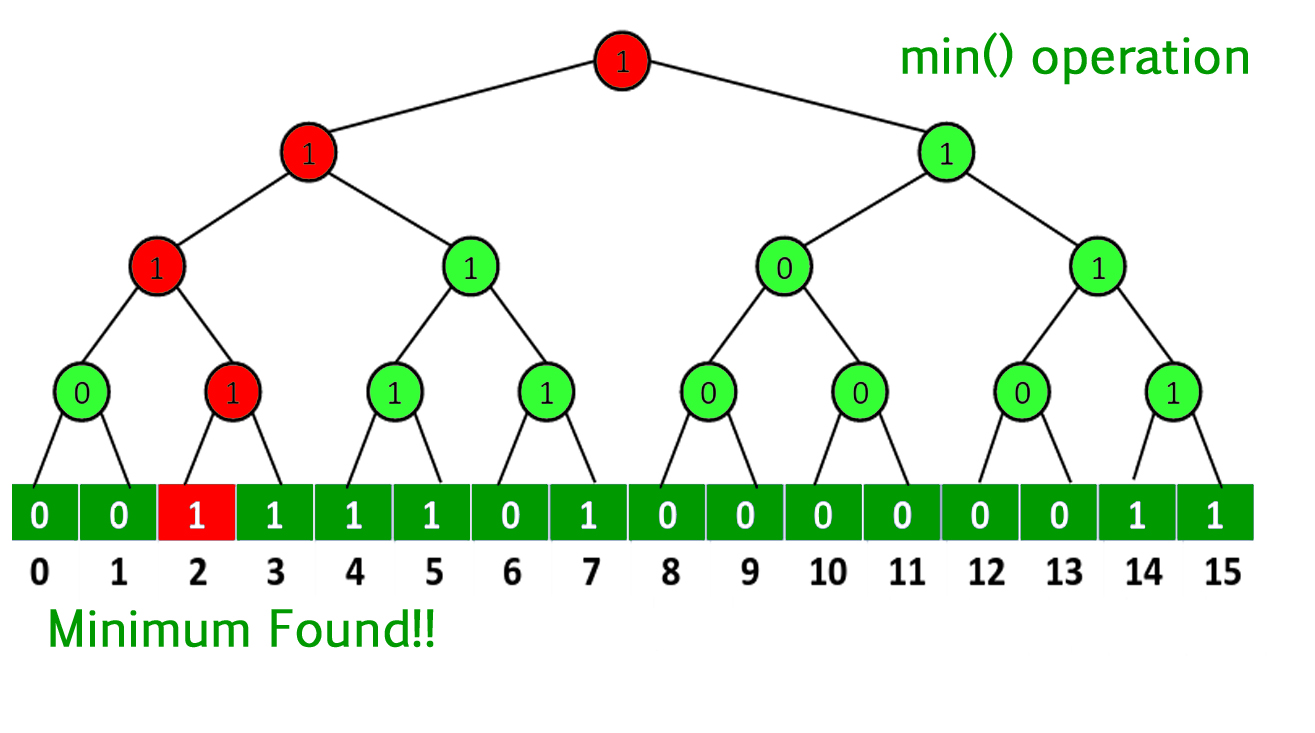 Since we travel across height of binary tree with u leaves, time complexity is reduced to O(Log u)
Since we travel across height of binary tree with u leaves, time complexity is reduced to O(Log u)
- max() : Similar to min(). Instead of left child, we prefer tight child.
- successor(x) : Start with leaf node indexed with x and travel towards the root until we reach a node z whose right child is 1 and not on the same path covered up until now. Stop at z and travel down to a leaf following the leftmost node with value 1.
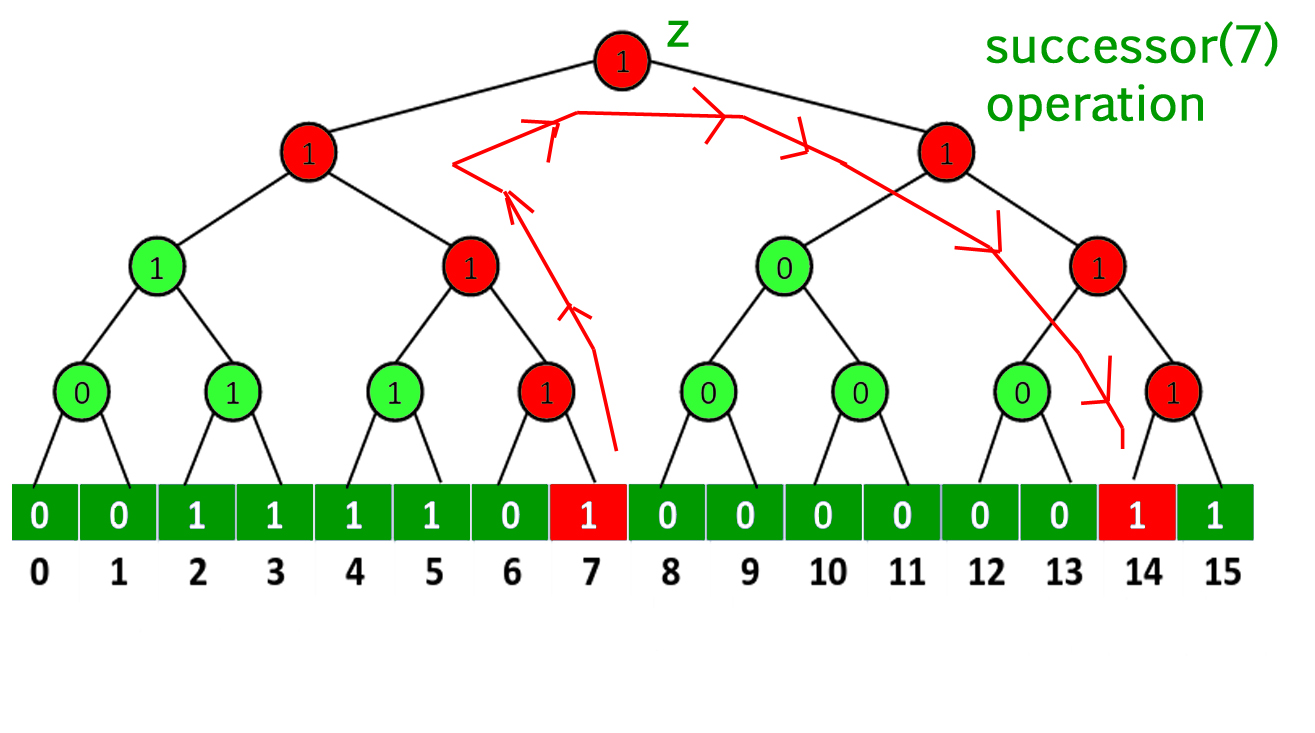
- predecessor() : This operation is similar to successor. Here we replace left with right and right with left in successor().
- find() is still O(1) as we still have binary array as leaves. insert() and delete() are now O(Log u) as we need to update internal nodes. In case of insert, we mark the corresponding leaf as 1, we traverse up and keep updating ancestors to 1 if they were 0.
proto van Emde Boas Tree We have seen that superimposing a binary tree over binary array reduces time complexity of max(), min(), successor() and predecessor() to O(Log u). Can we reduce this time complexity further to O(Log Log u)? The idea is to have varying degree at different levels. The root node (first level) covers whole universe. Every node of second level (next to root) covers u1/2 elements of universe. Every node of third level covers u1/4 elements and so on. With above recursive structure, we get time complexities of operations using below recursion.
T(u) = T(?u) + O(1)
Solution of this recurrence is,
T(u) = O(Log Log u)
Refer this for detailed steps to
get the above result.
Recursive definition of proto van Emde Boas Tree: Let u = 22k be the size of universe for some k >= 0.
- If u = 2, then it is a bias size tree contains only a binary array of size 2.
- Otherwise split the universe into ?(u1/2) blocks of size ?(u1/2) each and add a summary structure to the top.
We perform all queries as using the approach described in background. In this post, we have introduced the idea that is to superimpose tree structure on Binary Array such that nodes of different levels of the tree have varying degrees.
We will soon be discussing following in coming sets.
1) Detailed representation.
2) How to optimize max() and min() to work in O(1)?
3) Implementation of the above operations.
Sources: http://www-di.inf.puc-rio.br/~laber/vanEmdeBoas.pdf http://web.stanford.edu/class/cs166/lectures/14/Small14.pdf
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...