Proto Van Emde Boas Tree | Set 2 | Construction
Last Updated :
18 Apr, 2023
Van Emde Boas Tree supports search, minimum, maximum, successor, predecessor, insert and delete operations in O(lglgN) time which is faster than any of related data structures like priority queue, binary search tree, etc. Proto Van Emde Boas tree is similar prototype type data structure but it fails to achieve the complexity of O(lglgN), We will learn Proto Van Emde Boas tree first to get a basic understanding of working of Van Emde Boas tree. Here N is the size of the universe over which tree is defined.
Note: Proto Van Emde Boas Data Structure’s keys must be defined over a range of 0 to n(n is positive integer of the form 22k) and it works when duplicate keys are not allowed.
Abbreviations:
- Proto-VEB is an abbreviation of Proto-Van Emde Boas tree.
- Proto-VEB(
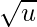 ) is an abbreviation for Proto-VEB containing u number of keys.
) is an abbreviation for Proto-VEB containing u number of keys.
Basic Understanding of the structure of Proto-VEB Tree:
Proto Van Emde boas tree are recursively defined data structure and it shrinks to sqrt size as we go up in the tree. Please refer this article to understand the basics of it.
In Proto-VEB we use a bit array to represents whether a key is present or not, we put 1 if it is present and 0 else.
Here, the summary of a particular cluster contains whether there is any key present in a cluster if at least one key present then the summary is 1 or 0 elsewhere. Clusters are segments of a bit array. A summary is also a bit array. See the image below:
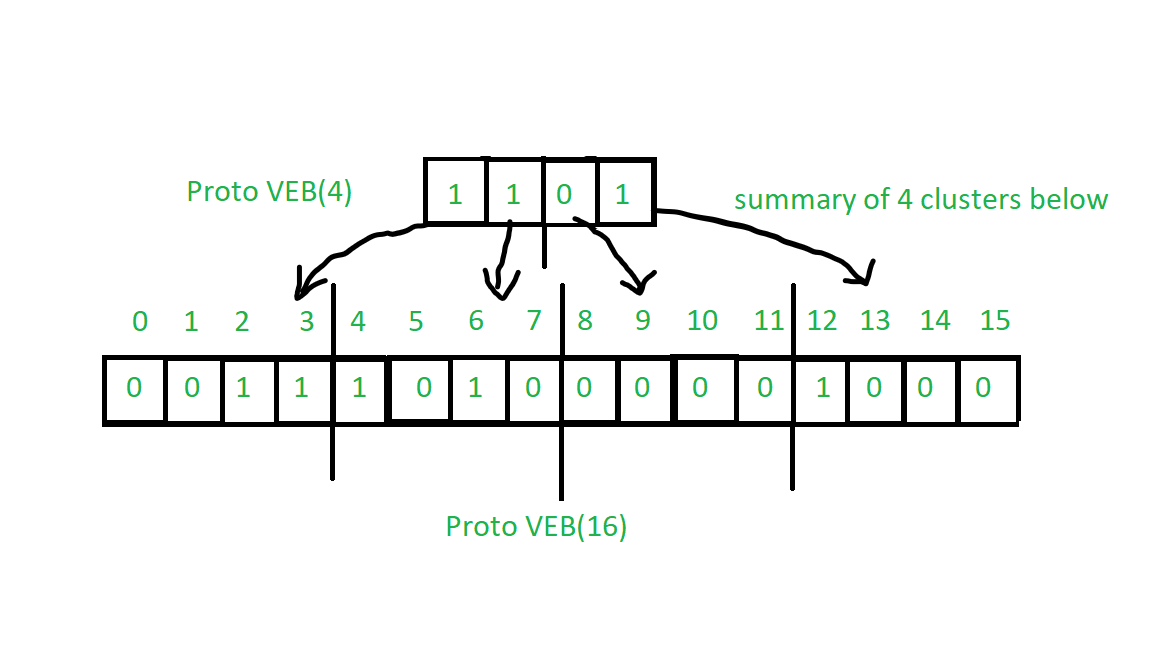
Construction of Proto VEB Tree:
Below image represents the basic Proto-VEB structure:
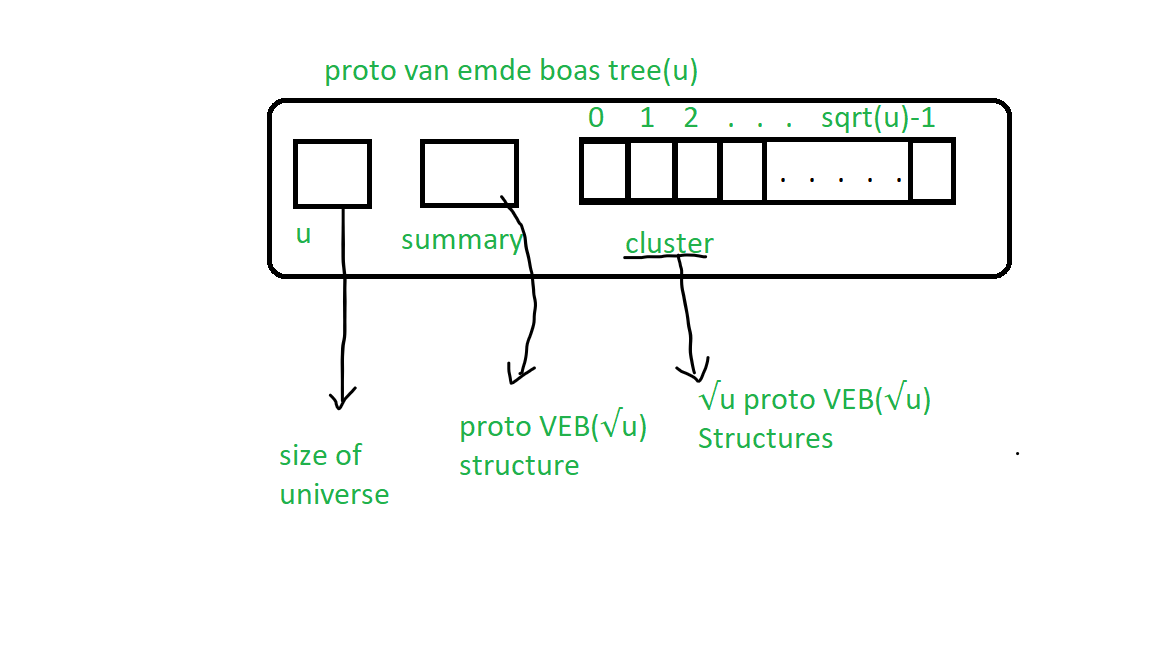
The recursively defined structure has two main part:
- summary: it is a pointer to Proto-VEB structure which has
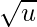 size.
size. - cluster: it is an array of pointers to Proto-VEB structures with
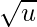 size.
size.
First of all, we have to understand some function and keywords:
- universe size (u) : Number of keys in Proto-VEB structure.
- High(x): From the first image, we can see that if we want to reach at the cluster of the key then we can divide it with
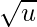 .
.
For example, We want to know the cluster of the key 12 then can divide it with 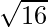 which is 3, so key 12 is in 3rd cluster.
which is 3, so key 12 is in 3rd cluster.
High(x) = floor( x / 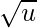 )
)
- low(x): From the first image, we can see that if we want the position of the key in the cluster we can apply modulus operation x %
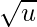 .
.
For example, If you want to find a position of 7 in the cluster you can apply 7 % 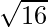 = 3 which is a position of 7 in 2nd cluster.
= 3 which is a position of 7 in 2nd cluster.
low(x) = x % 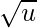 )
)
Recursive Procedure of construction:
- Base case : If universe size is 2 then it is a base size so there will be no more summary array, which means it is null and we will store only bit array for 2 keys.
- We will recursively assign summary as
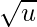 sized Proto-VEB tree and
sized Proto-VEB tree and 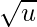 -sized Proto-VEB to all
-sized Proto-VEB to all 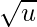 clusters.
clusters.
See u=4 Proto-VEB structure in the image below:
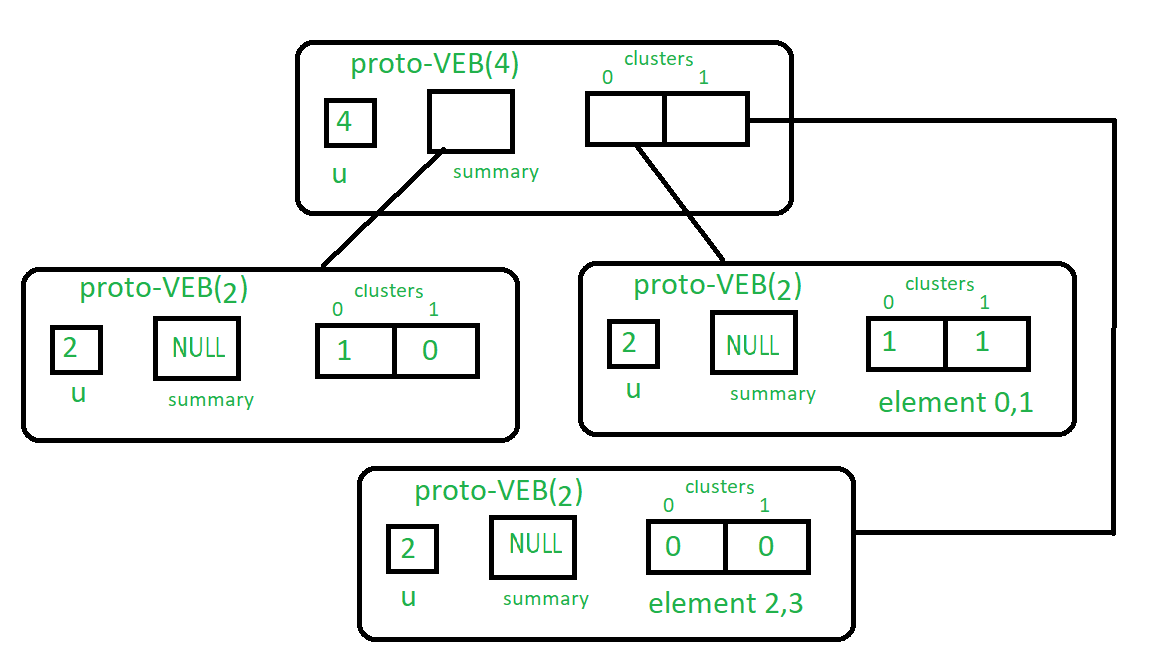
Here is the code representing the Algorithm:
C++
#include <bits/stdc++.h>
using namespace std;
class Proto_Van_Emde_Boas {
public:
int universe_size;
Proto_Van_Emde_Boas* summary;
vector<Proto_Van_Emde_Boas*> clusters;
int root(int u)
{
return (int)sqrt(u);
}
int high(int x)
{
return x / root(universe_size);
}
int low(int x)
{
return x % root(universe_size);
}
int generate_index(int cluster, int position)
{
return cluster * root(universe_size) + position;
}
Proto_Van_Emde_Boas(int size)
{
universe_size = size;
if (size <= 2) {
summary = nullptr;
clusters = vector<Proto_Van_Emde_Boas*>(size, nullptr);
}
else {
summary = new Proto_Van_Emde_Boas(root(size));
clusters = vector<Proto_Van_Emde_Boas*>(root(size), nullptr);
for (int i = 0; i < root(size); i++) {
clusters[i] = new Proto_Van_Emde_Boas(root(size));
}
}
}
};
int main()
{
Proto_Van_Emde_Boas pveb(4);
}
|
Java
import java.util.*;
class Proto_Van_Emde_Boas {
int universe_size;
Proto_Van_Emde_Boas summary;
ArrayList<Proto_Van_Emde_Boas> clusters;
int root(int u) { return (int)Math.sqrt(u); }
int high(int x) { return x / root(universe_size); }
int low(int x) { return x % root(universe_size); }
int generate_index(int cluster, int position)
{
return cluster * root(universe_size) + position;
}
Proto_Van_Emde_Boas(int size)
{
universe_size = size;
if (size <= 2) {
summary = null;
clusters
= new ArrayList<Proto_Van_Emde_Boas>(size);
for (int i = 0; i < size; i++) {
clusters.add(null);
}
}
else {
summary = new Proto_Van_Emde_Boas(root(size));
clusters = new ArrayList<Proto_Van_Emde_Boas>(
root(size));
for (int i = 0; i < root(size); i++) {
clusters.add(null);
}
for (int i = 0; i < root(size); i++) {
clusters.set(
i, new Proto_Van_Emde_Boas(root(size)));
}
}
}
}
class Main {
public static void main(String[] args)
{
Proto_Van_Emde_Boas pveb
= new Proto_Van_Emde_Boas(4);
}
}
|
C#
using System;
using System.Collections.Generic;
class Proto_Van_Emde_Boas
{
public int universe_size;
public Proto_Van_Emde_Boas summary;
public List<Proto_Van_Emde_Boas> clusters;
public Proto_Van_Emde_Boas(int size)
{
universe_size = size;
if (size <= 2)
{
summary = null;
clusters = new List<Proto_Van_Emde_Boas>(size);
for (int i = 0; i < size; i++)
{
clusters.Add(null);
}
}
else
{
summary = new Proto_Van_Emde_Boas((int)Math.Sqrt(size));
clusters = new List<Proto_Van_Emde_Boas>((int)Math.Sqrt(size));
for (int i = 0; i < Math.Sqrt(size); i++)
{
clusters.Add(new Proto_Van_Emde_Boas((int)Math.Sqrt(size)));
}
}
}
public int root(int u)
{
return (int)Math.Sqrt(u);
}
public int high(int x)
{
return x / root(universe_size);
}
public int low(int x)
{
return x % root(universe_size);
}
public int generate_index(int cluster, int position)
{
return cluster * root(universe_size) + position;
}
}
class Program
{
static void Main(string[] args)
{
Proto_Van_Emde_Boas pveb = new Proto_Van_Emde_Boas(4);
}
}
|
Python3
from typing import List
class Proto_Van_Emde_Boas:
def __init__(self, size: int):
self.universe_size = size
if size <= 2:
self.summary = None
self.clusters: List[Proto_Van_Emde_Boas] = [None] * size
else:
self.summary = Proto_Van_Emde_Boas(self.root(size))
self.clusters: List[Proto_Van_Emde_Boas] = [None] * self.root(size)
for i in range(self.root(size)):
self.clusters[i] = Proto_Van_Emde_Boas(self.root(size))
def root(self, u: int) -> int:
return int(u ** 0.5)
def high(self, x: int) -> int:
return x // self.root(self.universe_size)
def low(self, x: int) -> int:
return x % self.root(self.universe_size)
def generate_index(self, cluster: int, position: int) -> int:
return cluster * self.root(self.universe_size) + position
if __name__ == '__main__':
pveb = Proto_Van_Emde_Boas(4)
|
Javascript
class Proto_Van_Emde_Boas {
constructor(size) {
this.universe_size = size;
if (size <= 2) {
this.summary = null;
this.clusters = new Array(size).fill(null);
} else {
this.summary = new Proto_Van_Emde_Boas(this.root(size));
this.clusters = new Array(this.root(size)).fill(null).map(() => new Proto_Van_Emde_Boas(this.root(size)));
}
}
root(u) {
return Math.sqrt(u) | 0;
}
high(x) {
return (x / this.root(this.universe_size)) | 0;
}
low(x) {
return x % this.root(this.universe_size);
}
generate_index(cluster, position) {
return cluster * this.root(this.universe_size) + position;
}
}
let pveb = new Proto_Van_Emde_Boas(4);
|
Time Complexity : O(sqrt(n))
Share your thoughts in the comments
Please Login to comment...