Uni-variate Optimization – Data Science
Last Updated :
10 Jun, 2023
Optimization is an important part of any data science project, with the help of optimization we try to find the best parameters for our machine learning model which will give the minimum loss value. There can be several ways of minimizing the loss function, However, generally, we use variations of the gradient method for our optimization. In this article, we will discuss univariate optimization.
What is Univariate Optimization
Univariate optimization refers to the process of finding the optimal value of a function of a single independent variable within a given problem. It involves optimizing a function with respect to a single variable while keeping all other variables fixed.
In univariate analysis generally, there is an objective function like the profit of the object, the distance between two places, or determining the maximum or lowest value of a mathematical function. The mathematical structure for the optimization function is as:
minimize f(x), w.r.t x,
subject to a < x < b
where,
f(x) : Objective function
x : Decision variable
a < x < b : Constraint
Types of Optimization
Depending on the types of constraints optimization may be categorized into two parts
- Constrained optimization problems: In cases where the constraint is given there and we have to have the solution satisfy these constraints we call them constrained optimization problems.
- Unconstrained optimization problems: In cases where the constraint is missing we call them unconstrained optimization problems.
Terms Used in Univariate Optimization
There are several mathematical terms that we use frequently during optimizing a univariate function. These are as:
- Objective function: It is a mathematical function denoted by f(x) which we are optimizing to find the maximum or minimum value of it.
- Decision Variable: The decision variables are the feature/independent variable that we are using to optimize our objective function
- Feasible Reason: The feasible reason is that reason which our function can take while satisfying the contained used on it.
- Global Optimum: Global region is a point in the feasible region that has optimum value out of all the points present in the feasible region
- Local Optimum: These are the points in the feasible region of the objective function which is optimal than its neighbors but not be the global optimum.
- Derivative: Derivative is defined as the rate of change of an objective function at a specific point with respect to the independent features.
- Gradient: A gradient is defined as the partial derivative of the objective function with respect to the decision variable.
- Critical Points: These are the value of the decision variable at which either the gradient is zero or it is undefined.
- Convexity: It is the property of a function in which the line connecting any two points in the feasible region of a function lies above the objective function graph.
- Concavity: It is the opposite of convexity in which the line connecting the two points in the feasible region of a function lies below the function graph.
Steps To Calculate Univariate Optimization
- First, we define the objective function F(X) that we want to optimize
- Second, we decide our optimization whether we want to minimize or maximize our objective function.
- Third, we identify whether is there any constraint present in our problem statement on the decision variable.
- Fourth, we decide which Optimization Algorithm we will use to optimize our objective function.
- Fifth, we will apply the optimization algorithm and also choose our convergence criteria like the number of iterations, step size of the optimization algorithm
- In the last step, we will validate analyze and refine the result of the optimization algorithm we will see if can we change some hyperparameters to get better optimized results.
Necessary and Sufficient Conditions for Univariate Optimization
The necessary and sufficient conditions for x to be the optimizer(minimizer/maximizer) of the function f(x). In the case of uni-variate optimization, the necessary and sufficient conditions for x to be the minimizer of the function f(x) are
- First-order necessary condition: f'(x) = 0
- Second-order sufficiency condition: f”(x) > 0 (For x to be minimum)
- Second-order sufficiency condition: f”(x) < 0 (For x to be maximum)
Mathematical implementation of Univariate Optimization
min f(x) w.r.t x
Given f(x) = 3x4 – 4x3 – 12x2 + 3
According to the first-order necessary condition which states that the minimum occurs at a critical point where the derivative of the function is zero or undefined
Taking the derivative with respect to x: 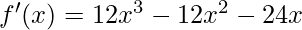
The equation to find the critical points: 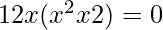
The quadratic equation: 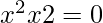
The solutions of the quadratic equation: 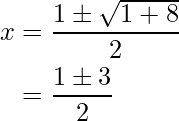
So, we have two critical points: x = -1 and x = 2. Now, we need to analyze the nature of these critical points to determine if they correspond to a minimum.
To do this, we can evaluate the second derivative of f(x):
Now, we want to know among these 3 values of x which are actually minimizers. To do so we look at the second-order sufficiency condition. So according to the second-order sufficiency condition:
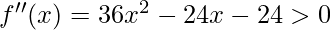
Putting each value of x in the above equation:
f”(x) | x = 0 = -24 (Don’t satisfy the sufficiency condition)
f”(x) | x = -1 = 36 > 0 (Satisfy the sufficiency condition)
f”(x) | x = 2 = 72 > 0 (Satisfy the sufficiency condition)
Hence -1 and 2 are the actual minimizer of f(x). So for these 2 values
f(x) | x = -1 = -2
f(x) | x = 2 = -29
Python implementation of Univariate Analysis
We can use scipy library to implement various mathematical functions. In our implementation, we will use minimize_scalar from the scipy optimize module to find the optimum function value of a custom-defined objective function.
Python3
import numpy as np
from scipy.optimize import minimize_scalar
def objective_function(x):
return x**2 + 3*x + 2
result = minimize_scalar(objective_function)
optimal_value = result.x
optimal_function_value = result.fun
print("Optimal value:", optimal_value)
print("Optimal function value:", optimal_function_value)
|
Output:
Optimal value: -1.5000000000000002
Optimal function value: -0.25
Share your thoughts in the comments
Please Login to comment...