Henry gas solubility optimization
Last Updated :
07 Jul, 2021
The method of identifying optimal settings for the specific parameters of a particular process of fulfilling all design objectives while considering the lowest feasible cost is referred to as an optimization. Problems with optimization can be seen in all areas science, so it is vital to design new optimization algorithms. Otherwise, standard optimization algorithms have several constraints, including single-based solutions, local optimization, and unknown search space problems. In order to overcome these constraints many scientists and researchers have created numerous metaheuristics to handle these restrictions in order to handle the problem/solved optimization. Metaheuristic algorithms tackle optimization issues by imitating phenomena of the ethological, biological or physical aspects. Metaheuristic algorithms can be classified into four categories namely:
- Swarm-intelligence-based algorithms;
- Evolutionary algorithms
- Natural science-based algorithms
- Natural phenomena-based algorithms
Henry Gas Solubility optimization (HGSO) comes under the Natural science-based algorithms as it imitates the behavior of gases according to the Henry’s law of gases.
Inspiration
HGSO is based on Henry’s law of gases. Henry’s law states that:
‘‘At a constant temperature, the amount of a given gas that dissolves in a given type and volume of liquid is directly proportional to the partial pressure of that gas in equilibrium with that liquid’’.
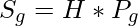
Where Sg ,Pg ,H denote the solubility of the gas, partial pressure of the gas and Henry’s constant (specific to a gas-solvent combination at a given temperature).
Henry’s constant change with the variation in temperature which can be shown using Van’t Hoff’s equation:
di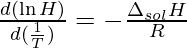 (1)
(1)
where \Delta_{sol} H denotes the enthalpy of dissolution, R is the gas constant. We can integrate the above equation to get:
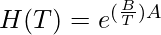 (2)
(2)
H is a function of T with A and B as parameters. Equation (2) can be rewritten for constant temperature T=298.15 K as:
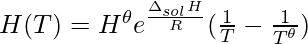 (3)
(3)
as \Delta_{sol} H} and R is a constant equation becomes
H(![Rendered by QuickLaTeX.com H(T) = H^\theta e^{(-c[\frac{1}{T}-\frac{1}{T^\theta}])}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-12ac531106486ddd7bcbce49aad8987a_l3.png) (4)
(4)
Mathematical Model
The mathematical model is defined as follows:
Initialization
At a given iteration time t we take N population of a gas and define the position of ith gas as:
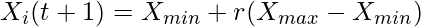
where r ranges between (0-1] and Xmax , Xmin are the bounds of the problems
So for a gas i in cluster j, we define Pi,j as its partial pressure, 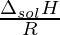 as a constant j(Ci) and Henry’s constant as j(Hj(t)) according to the equation:
as a constant j(Ci) and Henry’s constant as j(Hj(t)) according to the equation:
Hj(t) = q1r ; Pi,j = q2r ; Cj = q3r
where q1,q2,q3 are constants with values 0.005, 100, and 0.01 respectively.
Clustering
The gases are divided into clusters with same gas type. As there are same gases in any cluster taken at random, Hj would be constant.
Evaluation
The best gas in defined as the one which achieves highest equilibrium state. So for each cluster j we choose the best gas and the gases are ranked in order to find optimal gas in the entire clusters (swarm).
Updating parameters
The henry’s constant is updated according equation (4) at time t=t+1
![Rendered by QuickLaTeX.com H_j(t+1) = H_j(t) e^{(-C_j[\frac{1}{T(t)}-\frac{1}{T^\theta}])}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8d44e312ac4bd0db8eec5c9e5cf2b7b8_l3.png)
where T(t) = 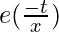
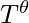 = 298.15k and x is the number of iteration
= 298.15k and x is the number of iteration
The solubility is updated as:
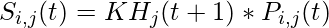
where Si,j(t), Pi,j(t) is the solubility , partial pressure of a gas i in cluster j at time t, K is a constant.
The position for t+1 is updated as:
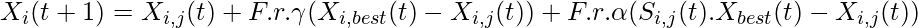
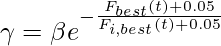
Where Xi,j is the position of a gas i in the cluster j, Si,j is the solubility of a gas i in cluster j at time t, Xi,best is the position of the best gas i in cluster j, Xbest is the best gas in all clusters/swarm, 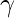 is the ability of a gas i in cluster j to interact with other gases in the same cluster,
is the ability of a gas i in cluster j to interact with other gases in the same cluster, 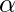 is the ability of other gases to interact with the gas i in cluster j,
is the ability of other gases to interact with the gas i in cluster j, 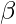 is a constant.
is a constant.
Rank worst agents
Select and rank up worst agent (Nw) according to equation:
![Rendered by QuickLaTeX.com N_w = N[r(c_2-c_1)+c_1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-10e42ff157ed6f51c78ff3d773cf3fd7_l3.png)
where N is the number of worst agents and c1 ,c2 are constants with values equal to 0.1,0.2
Update the positions of worst agents
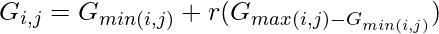
where Gi,j is the position of the gas i in cluster j and Gmax, Gmin are the bounds of the problem.
Return the best Gas
Xbest
This is how Henry’s gas solubility optimization works.
Share your thoughts in the comments
Please Login to comment...