Pathfinder Optimization Algorithm
Last Updated :
06 Oct, 2021
Nature is full of social behaviours for performing different tasks. Although the ultimate goal of all individuals and collective behaviours is survival, creatures cooperate and interact in groups, herds, schools, colonies, and flocks for several reasons: hunting, defending, navigating, and foraging. In order to mimic these characteristics of animals, swarm-intelligence based optimization algorithms are introduced.
For example – Ant Colony optimization, Cat Swarm Optimization, Particle Swarm optimization
Inspiration
A pathfinder simply is the individual which leads a swarm. This entity leads the swarm and this entity leads various acts. In addition, this entity takes the swarm to destinations including pastures, water and feeding areas. The group of animals frequently decide the movement between members via social order. Such animals may either have to decide with the leader or with no leader. Leadership however is temporary, with few people knowing the place, hunting area, route, etc.
Mathematical Model
The population basically follows the pathfinder for various activities. However, in order to do so, we need to specify the position of both the pathfinder and any arbitrary population member. The position of a member says Xi is defined as:
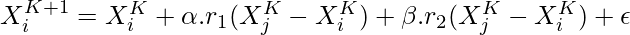
Where Xi is the position vector of ith follower at k iteration, r1 and r2 are random variables uniformly generated in the range of [0,1], α is the coefficient for interaction and β is the coefficient of attraction. The value of α, ß are set in such a way that there is the perfect balance between interaction (i.e. the magnitude of movement of any member together with its neighbour) and attraction (i.e. the random distance for keeping the herd roughly with the leader). The optimum values for α, ß should be around 1. ε is the vector of vibration and it is defined as follows:

where, 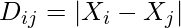 , u1 is random variable in range [-1,1]
, u1 is random variable in range [-1,1]
The position of pathfinder is defined as:

Xp is the position vector of the pathfinder, K is the current iteration, r3 if a random variable in the range of [0,1], A is the vector of fluctuation rate. A is defined as follows:
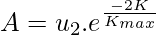
where u2 is a random variable in the range [-1,1], Kmax is the maximum iteration.
ε, A can provide random movement (walk) for all members. Therefore setting different values for them ensures exploration and exploitation. The term 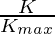 in ε, A ensures exploration and exploitation phases of a metaheuristic technique. At first
in ε, A ensures exploration and exploitation phases of a metaheuristic technique. At first 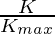 is very small, thereby resulting in rapid change constituting to exploration. Then at later stages, its value becomes eventually small or even zero, constituting exploitation.
is very small, thereby resulting in rapid change constituting to exploration. Then at later stages, its value becomes eventually small or even zero, constituting exploitation.
Algorithm
- Define the parameters such as r1, r2, ε, A
- Initialize the population and calculate fitness for each member
- Set the best fitness value as the pathfinder
- while iteration condition is not met or till max iteration do
- Generate α, ß in range [0, 1]
- Using the pathfinder equation update the position of pathfinder
- If fitness of current pathfinder is better than old pathfinder Then
- Update fitness of the pathfinder
- For i=1 to population size
- Update position of followers using followers equation.
- Update fitness values of each member
- Find the best fitness
- If best fitness is better than old pathfinder Then
- Update fitness of the pathfinder
- For i=1 to population size
- If new fitness of the member is better than old fitness Then
- Update fitness of member
- Generate ε, A
- End
The best position and fitness is returned and can be used to solve optimization problems.
References: https://www.sciencedirect.com/science/article/pii/S1568494619301309
Share your thoughts in the comments
Please Login to comment...