Total number of Subsets of size at most K
Last Updated :
21 Jan, 2022
Given a number N which is the size of the set and a number K, the task is to find the count of subsets, of the set of N elements, having at most K elements in it, i.e. the size of subset is less than or equal to K.
Examples:
Input: N = 3, K = 2
Output: 6
Subsets with 1 element in it = {1}, {2}, {3}
Subsets with 2 elements in it = {1, 2}, {1, 3}, {1, 2}
Since K = 2, therefore only the above subsets will be considered for length atmost K. Therefore the count is 6.
Input: N = 5, K = 2
Output: 15
Approach:
- Since the number of subsets of exactly K elements that can be made from N items is (NCK). Therefore for “at most”, the required count will be
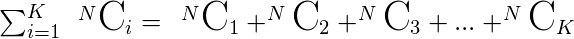
- Inorder to calculate the value of NCK, Binomial Coefficient is used. Please refer this article to see how it works.
- So to get the required subsets for length atmost K, run a loop from 1 to K and add the NCi for each value of i.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int binomialCoeff(int n, int k)
{
int C[n + 1][k + 1];
int i, j;
for (i = 0; i <= n; i++) {
for (j = 0; j <= min(i, k); j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
return C[n][k];
}
int count(int n, int k)
{
int sum = 0;
for (int j = 1; j <= k; j++) {
sum = sum + binomialCoeff(n, j);
}
return sum;
}
int main()
{
int n = 3, k = 2;
cout << count(n, k) << endl;
n = 5, k = 2;
cout << count(n, k) << endl;
return 0;
}
|
Java
import java.lang.*;
class GFG
{
public static int binomialCoeff(int n, int k)
{
int[][] C = new int[n + 1][k + 1];
int i, j;
for (i = 0; i <= n; i++)
{
for (j = 0; j <= Math.min(i, k); j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
return C[n][k];
}
public static int count(int n, int k)
{
int sum = 0;
for (int j = 1; j <= k; j++)
{
sum = sum + binomialCoeff(n, j);
}
return sum;
}
public static void main(String args[])
{
GFG g = new GFG();
int n = 3, k = 2;
System.out.print(count(n, k));
int n1 = 5, k1 = 2;
System.out.print(count(n1, k1));
}
}
|
Python3
def binomialCoeff(n, k):
C = [[0 for i in range(k + 1)] for j in range(n + 1)];
i, j = 0, 0;
for i in range(n + 1):
for j in range( min(i, k) + 1):
if (j == 0 or j == i):
C[i][j] = 1;
else:
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
return C[n][k];
def count(n, k):
sum = 0;
for j in range(1, k+1):
sum = sum + binomialCoeff(n, j);
return sum;
if __name__ == '__main__':
n = 3;
k = 2;
print(count(n, k), end="");
n1 = 5;
k1 = 2;
print(count(n1, k1));
|
C#
using System;
class GFG
{
public static int binomialCoeff(int n, int k)
{
int[,] C = new int[n + 1, k + 1];
int i, j;
for (i = 0; i <= n; i++)
{
for (j = 0; j <= Math.Min(i, k); j++)
{
if (j == 0 || j == i)
C[i, j] = 1;
else
C[i, j] = C[i - 1, j - 1] + C[i - 1, j];
}
}
return C[n, k];
}
public static int count(int n, int k)
{
int sum = 0;
for (int j = 1; j <= k; j++)
{
sum = sum + binomialCoeff(n, j);
}
return sum;
}
public static void Main()
{
int n = 3, k = 2;
Console.Write(count(n, k));
int n1 = 5, k1 = 2;
Console.Write(count(n1, k1));
}
}
|
Javascript
<script>
function binomialCoeff(n, k)
{
var C = new Array(n + 1);
for (var i = 0; i < C.length; i++) {
C[i] = new Array(k + 1);
}
var i, j;
for (i = 0; i <= n; i++) {
for (j = 0; j <= Math.min(i, k); j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
return C[n][k];
}
function count(n, k)
{
var sum = 0;
for (var j = 1; j <= k; j++) {
sum = sum + binomialCoeff(n, j);
}
return sum;
}
var n = 3;
var k = 2;
document.write(count(n, k));
var n = 5;
var k = 2;
document.write(count(n, k));
</script>
|
Time Complexity: O(n2 * k)
Auxiliary Space: O(n + k)
Share your thoughts in the comments
Please Login to comment...