Up until the 18th century, the light was considered to be a ray that traveled in a straight line. Descartes gave the corpuscular model of light which was further developed by Isaac Newton to include the laws of reflection and refraction. Later, a Dutch physicist introduced a new model of light which modeled light as a wave. This model was not widely accepted because of Newton’s authority and almost negligible experimental evidence. However, due to Thomas Young’s experiments, it was established that light possesses a wave nature. Since it was established that light has a wave nature, the study of interference and superposition became an essential part of this field. Let’s study these concepts in detail.
Principle of Superposition
When more than one waves travel in the same medium, they are bound to interact with each other. The superposition principle helps us describe the resulting wave or motion that is produced when two or more waves combine with each other. The figure below shows two waves that are producing some displacement in the particles of the given medium. In this case, the principle of superposition states that,
The resultant displacement of a number of waves in the medium at a particular point is the vector sum of the individual displacements produced by wave at each point.

The principles of superposition can be applied to any type of waves provided that:
- The waves that are superimposed are of the same types.
- The medium in which the waves are propagating behaves linearly, this means that the particles of the medium which are displaced with twice the displacement experience twice the amount of restoring force on them.
Light waves travel at different speeds in different media, the velocity changes but the frequency remains the same. Now since the velocity of the wave is changing while the frequency remains the same. It can be concluded that the wavelength of the wave also changes when light travels through different mediums. In case, the wave which is getting superimposed is traveling in the same direction, it is called coherent addition and vice-versa for the incoherent addition.
Interference of Waves
Consider two needles kept in the water and points S1 and S2 as shown in the figure. These needles are moving up and down periodically in an identical fashion. This motion produces two water waves and assuming that at a particular point the phase difference between these waves does not change with time. Thus, the two sources can be termed coherent sources.

Constructive Interference
In the figure given above, consider the point P which is at an equal distance from both of the needles. This interference can be observed almost everywhere in real life where waves are at play. In this case, usually, the intensity of the resulting wave is more than the individual intensities of the waves which are superimposed on each other. This phenomenon is exploited in engineering fields like communications engineering and optics.
PS1 = PS2
Since the two waves travel at an equal velocity, these waves take equal time to reach point P. The displacement produced due to each wave is given by
y1 = acos(ωt)
y2 = acos(ωt)
Now using the principle of superposition to find the resultant displacement (y).
y = y1 + y2
⇒ y = acos(ωt) + acos(ωt)
⇒ y = 2acos(ωt)
It’s already known that the intensity is proportional to the square of the amplitude. So, now since the amplitude becomes twice the original amplitude. If the initial intensity is considered as I0, intensity after the superposition will be given by,
I = 4I0
Since the intensity is increasing after the superposition. This is termed constructive interference. Now let’s take another similar example for this case, consider point Q given in the figure below. Assuming the wavelength for the wave \lambda, the path difference in this case is,

S1Q – S2Q = 2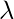
Notice in the figure that the wave originating from the point S1 reaches the point Q exactly two cycles earlier. The displacement produced at this point by individual waves will be given by,
y1 = acos(ωt)
y2 = acos(ωt – 4π)
y = y1 + y2
⇒ y = acos(ωt) + acos(ωt – 4π)
⇒.y = acos(ωt) + acos(ωt)
⇒ y = 2acos(ωt)
Notice that the path difference of 2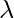 gives us a constructive interference. Thus in a more general way, it can be said that the path difference of
gives us a constructive interference. Thus in a more general way, it can be said that the path difference of 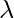 n gives us the constructive interference. Here n = 0, 1, 2, 3, …
n gives us the constructive interference. Here n = 0, 1, 2, 3, …
Destructive Interference
This kind of interference usually occurs at places which the displacements are usually in the opposite directions, the net effect of the superposition of the waves reduces the amplitude and intensity of the resulting wave. Similar to the previous cases, let us consider a point R given in the figure below. The path difference between these paths is given as 2.5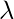

S2R – S1R = -2.5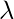
Thus, the waves originating from S1 the two points will reach exactly two and a half cycles later. Thus, in that case the phase difference becomes 5π.
y1 = acos(ωt)
y2 = acos(ωt + 5π)
y = y1 + y2
⇒ y = acos(ωt) + acos(ωt + 5π)
⇒.y = acos(ωt) – acos(ωt)
⇒ y = 0
So, this time two displacements in opposite directions resulted in zero amplitude and zero intensity. This is called destructive interference. The path difference in destructive interference can be generalised to (n + 0.5)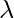 where n = 0, 1, 2, 3 ….
where n = 0, 1, 2, 3 ….
Let’s see some examples of these concepts.
Sample Problems
Question 1: The phenomena of interference can be explained by which of the following principles:
- Heisenberg Principle
- Fermi Principle
- Superposition Principle
- Quantum Mechanics
Answer:
Phenomena of interference can be explained by “Superposition Principle”. It states that,
“The resultant displacement of a number of waves in the medium at a particular point is the vector sum of the individual displacements produced by wave at each point.”
Question 2: Two waves travelling in a medium are given by the following equations,
y1 = acos(ωt)
y2 = acos(ωt + π)
Find the resulting amplitude after their superposition.
Answer:
y = acos(ωt)+acos(ωt+π)
⇒ y = acos(ωt)−acos(ωt)
⇒ y = 0
The resulting amplitude becomes zero.
Question 3: Two waves travelling in a medium are given by the following equations,
y1 = acos(ωt)
y2 = acos(ωt + 2π)
Find the resulting amplitude after their superposition.
Answer:
y = acos(ωt)+acos(ωt+2π)
⇒ y = acos(ωt)+acos(ωt)
⇒ y = 2acos(ωt)
The resulting amplitude becomes “2a”.
Question 4: Two waves travelling in a medium are given by the following equations,
y1 = 2acos(ωt)
y2 = acos(ωt + π)
Find the resulting amplitude after their superposition.
Answer:
y = 2acos(ωt)+acos(ωt+π)
⇒ y = 2acos(ωt)−acos(ωt)
⇒ y = acos(ωt)
Question 5: Two waves travelling in a medium are given by the following equations,
y1 = 5acos(ωt)
y2 =3acos(ωt + 2π)
Find the resulting amplitude after their superposition.
Answer:
y = 5acos(ωt)+3acos(ωt+2π)
⇒ y = 5acos(ωt)+3acos(ωt)
⇒ y = 8acos(ωt)
The resulting amplitude becomes “8a”.
Share your thoughts in the comments
Please Login to comment...