Sum of the series 3, 20, 63, 144, ……

Find the sum of first n terms of the given series:

3, 20, 63, 144, .....

Examples:

Input : n = 2
Output : 23

Input : n =4
Output : 230

Approach: 
First, we have to find the general term (Tn) of the given series. 

series can we written in the following way also:
(3 * 1^2), (5 * 2^2), (7 * 3^2), (9 * 4^2), .......up t n terms
Tn = (General term of series 3, 5, 7, 9 ....) X (General term of series 1^2, 2^2, 3^2, 4^2 ....)
Tn = (3 + (n-1) * 2) X ( n^2 )
Tn = 2*n^3 + n^2

We can write the sum of the series in the following ways: 

 Sn = 3 + 20 + 63 + 144 + ........up to the n terms
  
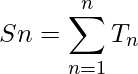
[Tex]$$
     Sn = 2 \times \sum_{n=1}^{n} n^{3} + \sum_{n=1}^{n} n^{2}
 $$[/Tex]Sn = 2 * (sum of n terms of n^3 ) + (sum of n terms of n^2)

Following are the formulas of sum of n terms of n^3 and n^2 : 

Below is the implementation of the above approach: 

C++

// C++ program to find the sum of n terms
#include <bits/stdc++.h>
using namespace std;
int calculateSum(int n)
{
    return (2 * pow((n * (n + 1) / 2), 2)) +
           ((n * (n + 1) * (2 * n + 1)) / 6);
}
int main()
{
    int n = 4;
    cout << "Sum = " << calculateSum(n) << endl;
    return 0;
}

Java

// Java program to find the sum of n terms
import java.io.*;

public class GFG
{
    static int calculateSum(int n)
    {
        return (int)((2 * Math.pow((n * (n + 1) / 2), 2))) +
               ((n * (n + 1) * (2 * n + 1)) / 6);
    }

    public static void main (String[] args) {

        int n = 4;
        System.out.println("Sum = " +  calculateSum(n));

    }
}
// This code is contributed by Raj

Python3

# Python3 program to find the sum of n terms

def calculateSum(n):
    return ((2 * (n * (n + 1) / 2)**2) +
           ((n * (n + 1) * (2 * n + 1)) / 6))

#Driver code

n = 4
print("Sum =",calculateSum(n))

# this code is contributed by Shashank_Sharma

C#

// C# program to find the sum of n terms
using System;

class GFG
{
static int calculateSum(int n)
{
    return (int)((2 * Math.Pow((n * (n + 1) / 2), 2))) +
                     ((n * (n + 1) * (2 * n + 1)) / 6);
}

// Driver Code
public static void Main ()
{
    int n = 4;
    Console.WriteLine("Sum = " + calculateSum(n));
}
}

// This code is contributed by anuj_67

PHP

<?php
// PHP program to find the
// sum of n terms

function calculateSum($n)
{
    return (2 * pow(($n * ($n + 1) / 2), 2)) +
           (($n * ($n + 1) * (2 * $n + 1)) / 6);
}

// Driver Code
$n = 4;
echo "Sum = " , calculateSum($n);

// This code is contributed by ash264
?>

Javascript

<script>

// javascript program to find the sum of n terms


function calculateSum(n)
{
    return parseInt(((2 * Math.pow((n * (n + 1) / 2), 2))) +
           ((n * (n + 1) * (2 * n + 1)) / 6));
}

var n = 4;
document.write("Sum = " +  calculateSum(n));

// This code contributed by shikhasingrajput
</script>

Output:

Sum = 230

Time Complexity: O(1)

Auxiliary Space: O(1)