Sum of all proper divisors from 1 to N

Given a positive integer N, the task is to find the value of 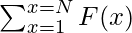where function F(x) can be defined as sum of all proper divisors of ‘x‘.
Examples:

Input: N = 4 
Output: 5 
Explanation:
Sum of all proper divisors of numbers: 
F(1) = 0 
F(2) = 1 
F(3) = 1 
F(4) = 1 + 2 = 3 
Total Sum = F(1) + F(2) + F(3) + F(4) = 0 + 1 + 1 + 3 = 5
Input: N = 5 
Output: 6 
Explanation:
Sum of all proper divisors of numbers: 
F(1) = 0 
F(2) = 1 
F(3) = 1 
F(4) = 1 + 2 = 3 
F(5) = 1 
Total Sum = F(1) + F(2) + F(3) + F(4) + F(5) = 0 + 1 + 1 + 3 + 1 = 6 

Naive approach: The idea is to find the sum of proper divisors of each number in the range [1, N] individually, and then add them to find the required sum.
Below is the implementation of the above approach:

C++

// C++ implementation to find sum of all
// proper divisor of number up to N
#include <bits/stdc++.h>
using namespace std;

// Utility function to find sum of
// all proper divisor of number up to N
int properDivisorSum(int n)
{
    int sum = 0;

    // Loop to iterate over all the
    // numbers from 1 to N
    for (int i = 1; i <= n; ++i) {

        // Find all divisors of
        // i and add them
        for (int j = 1; j * j <= i; ++j) {
            if (i % j == 0) {
                if (i / j == j)
                    sum += j;
                else
                    sum += j + i / j;
            }
        }

        // Subtracting 'i' so that the
        // number itself is not included
        sum = sum - i;
    }
    return sum;
}

// Driver Code
int main()
{
    int n = 4;
    cout << properDivisorSum(n) << endl;

    n = 5;
    cout << properDivisorSum(n) << endl;

    return 0;
}

Java

// Java implementation to find sum of all
// proper divisor of number up to N
class GFG {

    // Utility function to find sum of
    // all proper divisor of number up to N
    static int properDivisorSum(int n)
    {
        int sum = 0;

        // Loop to iterate over all the
        // numbers from 1 to N
        for (int i = 1; i <= n; ++i) {

            // Find all divisors of
            // i and add them
            for (int j = 1; j * j <= i; ++j) {
                if (i % j == 0) {
                    if (i / j == j)
                        sum += j;
                    else
                        sum += j + i / j;
                }
            }

            // Subtracting 'i' so that the
            // number itself is not included
            sum = sum - i;
        }
        return sum;
    }

    // Driver Code
    public static void main (String[] args)
    {
        int n = 4;
        System.out.println(properDivisorSum(n));

        n = 5;
        System.out.println(properDivisorSum(n)) ;

    }
}

// This code is contributed by Yash_R

Python3

# Python3 implementation to find sum of all
# proper divisor of number up to N

# Utility function to find sum of
# all proper divisor of number up to N
def properDivisorSum(n):

    sum = 0

    # Loop to iterate over all the
    # numbers from 1 to N
    for i in range(n+1):

        # Find all divisors of
        # i and add them
        for j in range(1, i + 1):
            if j * j > i:
                break
            if (i % j == 0):
                if (i // j == j):
                    sum += j
                else:
                    sum += j + i // j

        # Subtracting 'i' so that the
        # number itself is not included
        sum = sum - i

    return sum

# Driver Code
if __name__ == '__main__':

    n = 4
    print(properDivisorSum(n))

    n = 5
    print(properDivisorSum(n))

# This code is contributed by mohit kumar 29

C#

// C# implementation to find sum of all
// proper divisor of number up to N
using System;

class GFG {

    // Utility function to find sum of
    // all proper divisor of number up to N
    static int properDivisorSum(int n)
    {
        int sum = 0;

        // Loop to iterate over all the
        // numbers from 1 to N
        for (int i = 1; i <= n; ++i) {

            // Find all divisors of
            // i and add them
            for (int j = 1; j * j <= i; ++j) {
                if (i % j == 0) {
                    if (i / j == j)
                        sum += j;
                    else
                        sum += j + i / j;
                }
            }

            // Subtracting 'i' so that the
            // number itself is not included
            sum = sum - i;
        }
        return sum;
    }

    // Driver Code
    public static void Main (string[] args)
    {
        int n = 4;
        Console.WriteLine(properDivisorSum(n));

        n = 5;
        Console.WriteLine(properDivisorSum(n)) ;
    }
}

// This code is contributed by Yash_R

Javascript

<script>

//Javascript implementation to find sum of all
// proper divisor of number up to N

// Utility function to find sum of
// all proper divisor of number up to N
function properDivisorSum(n)
{
    let sum = 0;

    // Loop to iterate over all the
    // numbers from 1 to N
    for (let i = 1; i <= n; ++i) {

        // Find all divisors of
        // i and add them
        for (let j = 1; j * j <= i; ++j) {
            if (i % j == 0) {
                if (i / j == j)
                    sum += j;
                else
                    sum += j + i / j;
            }
        }

        // Subtracting 'i' so that the
        // number itself is not included
        sum = sum - i;
    }
    return sum;
}

// Driver Code

    let n = 4;
    document.write(properDivisorSum(n) + "<br>");

    n = 5;
    document.write(properDivisorSum(n) + "<br>");


// This code is contributed by Mayank Tyagi

</script>

Output:

5
6

Time complexity: O(N * ?N) 
Auxiliary space: O(1)
Efficient approach: Upon observing the pattern in the function, it can be seen that “For a given number N, every number ‘x’ in the range [1, N] occurs (N/x) number of times”.
For example:

Let N = 6 => G(N) = F(1) + F(2) + F(3) + F(4) + F(5) + F(6) 
x = 1 => 1 will occurs 6 times (in F(1), F(2), F(3), F(4), F(5) and F(6)) 
x = 2 => 2 will occurs 3 times (in F(2), F(4) and F(6)) 
x = 3 => 3 will occur 2 times (in F(3) and F(6)) 
x = 4 => 4 will occur 1 times (in F(4)) 
x = 5 => 5 will occur 1 times (in F(5)) 
x = 6 => 6 will occur 1 times (in F(6)) 

From above observation, it can easily be observed that number x occurs only in its multiple less than or equal to N. Therefore, we just need to find the count of such multiples, for each value of x in [1, N], and then multiply it with x. This value is then added to the final sum.
Below is the implementation of the above approach: 

C++

// C++ implementation to find sum of all
// proper divisor of numbers up to N

#include <bits/stdc++.h>
using namespace std;

// Utility function to find sum of
// all proper divisor of number up to N
int properDivisorSum(int n)
{
    int sum = 0;

    // Loop to find the proper
    // divisor of every number
    // from 1 to N
    for (int i = 1; i <= n; ++i)
        sum += (n / i) * i;

    return sum - n * (n + 1) / 2;
}

// Driver Code
int main()
{
    int n = 4;
    cout << properDivisorSum(n) << endl;

    n = 5;
    cout << properDivisorSum(n) << endl;
    return 0;
}

Java

// Java implementation to find sum of all
// proper divisor of numbers up to N

// Utility function to find sum of
// all proper divisor of number up to N

class GFG
{
    static int properDivisorSum(int n)
    {
        int sum = 0;
        int i;
        // Loop to find the proper
        // divisor of every number
        // from 1 to N
        for (i = 1; i <= n; ++i)
            sum += (n / i) * i;

        return sum - n * (n + 1) / 2;
    }

    // Driver Code
    public static void main(String []args)
    {
        int n = 4;
        System.out.println(properDivisorSum(n));

        n = 5;
        System.out.println(properDivisorSum(n));

    }
}

Python3

# Python3 implementation to find sum of all
# proper divisor of numbers up to N

# Utility function to find sum of
# all proper divisor of number up to N
def properDivisorSum(n):

    sum = 0

    # Loop to find the proper
    # divisor of every number
    # from 1 to N
    for i in range(1, n + 1):
        sum += (n // i) * i

    return sum - n * (n + 1) // 2


# Driver Code
n = 4
print(properDivisorSum(n))

n = 5
print(properDivisorSum(n))

# This code is contributed by shubhamsingh10

C#

// C# implementation to find sum of all
// proper divisor of numbers up to N

// Utility function to find sum of
// all proper divisor of number up to N
using System;

class GFG
{
    static int properDivisorSum(int n)
    {
        int sum = 0;
        int i;
        // Loop to find the proper
        // divisor of every number
        // from 1 to N
        for (i = 1; i <= n; ++i)
            sum += (n / i) * i;

        return sum - n * (n + 1) / 2;
    }

    // Driver Code
    public static void Main(String []args)
    {
        int n = 4;
        Console.WriteLine(properDivisorSum(n));

        n = 5;
        Console.WriteLine(properDivisorSum(n));

    }
}

// This code is contributed by 29AjayKumar

Javascript

<script>

// Javascript implementation to find sum of all
// proper divisor of numbers up to N

// Utility function to find sum of
// all proper divisor of number up to N
function properDivisorSum(n)
{
    var sum = 0;

    // Loop to find the proper
    // divisor of every number
    // from 1 to N
    for (var i = 1; i <= n; ++i)
        sum += parseInt(n / i) * i;

    return sum - n * ((n + 1) / 2);
}

// Driver Code
var n = 4;
document.write(properDivisorSum(n)+"<br>");
n = 5;
document.write(properDivisorSum(n)+"<br>");

// This code is contributed by rutvik_56.
</script>

Output:

5
6

Time complexity: O(N) 
Auxiliary space: O(1)