Some Basic Theorems on Trees
Last Updated :
06 Mar, 2023
Tree:- A connected graph without any circuit is called a Tree. In other words, a tree is an undirected graph G that satisfies any of the following equivalent conditions:
- Any two vertices in G can be connected by a unique simple path.
- G is acyclic, and a simple cycle is formed if any edge is added to G.
- G is connected and has no cycles.
- G is connected but would become disconnected if any single edge is removed from G.
- G is connected and the 3-vertex complete graph K3 is not a minor of G.
For Example:
- This Graph is a Tree:

- This Graph is not a Tree:

Some theorems related to trees are:
- Theorem 1: Prove that for a tree (T), there is one and only one path between every pair of vertices in a tree.
Proof: Since tree (T) is a connected graph, there exist at least one path between every pair of vertices in a tree (T). Now, suppose between two vertices a and b of the tree (T) there exist two paths. The union of these two paths will contain a circuit and tree (T) cannot be a tree. Hence the above statement is proved.

Figure 3: Tree(T)
- Theorem 2: If in a graph G there is one and only one path between every pair of vertices than graph G is a tree.
Proof: There is the existence of a path between every pair of vertices so we assume that graph G is connected. A circuit in a graph implies that there is at least one pair of vertices a and b, such that there are two distinct paths between a and b. Since G has one and only one path between every pair of vertices. G cannot have any circuit. Hence graph G is a tree.

Figure 4: Given graph G
- Theorem 3: Prove that a tree with n vertices has (n-1) edges.
Proof: Let n be the number of vertices in a tree (T).
If n=1, then the number of edges=0.
If n=2 then the number of edges=1.
If n=3 then the number of edges=2.
Hence, the statement (or result) is true for n=1, 2, 3.
Let the statement be true for n=m. Now we want to prove that it is true for n=m+1.
Let
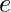 be the edge connecting vertices say Vi and Vj. Since G is a tree, then there exists only one path between vertices Vi and Vj. Hence if we delete edge e it will be disconnected graph into two components G1 and G2 say. These components have less than m+1 vertices and there is no circuit and hence each component G1 and G2 have m1 and m2 vertices.
be the edge connecting vertices say Vi and Vj. Since G is a tree, then there exists only one path between vertices Vi and Vj. Hence if we delete edge e it will be disconnected graph into two components G1 and G2 say. These components have less than m+1 vertices and there is no circuit and hence each component G1 and G2 have m1 and m2 vertices.
Now, the total no. of edges = (m1-1) + (m2-1) +1
= (m1+m2)-1
= m+1-1
= m.
Hence for n=m+1 vertices there are m edges in a tree (T). By the mathematical induction the graph exactly has n-1 edges.

Figure 5: Given a tree T
- Theorem 4: Prove that any connected graph G with n vertices and (n-1) edges is a tree.
Proof: We know that the minimum number of edges required to make a graph of n vertices connected is (n-1) edges. We can observe that removal of one edge from the graph G will make it disconnected. Thus a connected graph of n vertices and (n-1) edges cannot have a circuit. Hence a graph G is a tree.

Figure 6: Graph G
- Theorem 5: Prove that a graph with n vertices, (n-1) edges and no circuit is a connected graph.
Proof: Let the graph G is disconnected then there exist at least two components G1 and G2 say. Each of the component is circuit-less as G is circuit-less. Now to make a graph G connected we need to add one edge e between the vertices Vi and Vj, where Vi is the vertex of G1 and Vj is the vertex of component G2.
Now the number of edges in G = (n – 1)+1 =n.

Figure 7: Disconnected Graph

Figure 8:Connected graph G
- Theorem 6: A graph G is a tree if and only if it is minimally connected.
Proof: Let the graph G is minimally connected, i.e; removal of one edge make it disconnected. Therefore, there is no circuit. Hence graph G is a tree.
Conversely, let the graph G is a tree i.e; there exists one and only one path between every pair of vertices and we know that removal of one edge from the path makes the graph disconnected. Hence graph G is minimally connected.

Figure 9: Minimally Connected Graph
- Theorem 7: Every tree with at-least two vertices has at-least two pendant vertices.
Proof: Let the number of vertices in a given tree T is n and n>=2. Therefore the number of edges in a tree T=n-1 using above theorems.
summation of (deg(Vi)) = 2*e
= 2*(n-1)
=2n-2
The degree sum is to be divided among n vertices. Since a tree T is a connected graph, it cannot have a vertex of degree zero. Each vertex contributes at-least one to the above sum. Thus there must be at least two vertices of degree 1. Hence every tree with at-least two vertices have at-least two pendant vertices.

Figure 10: Here a, b and d are pendent vertices of the given graph
- Theorem 8: Show that every tree has either one or two centres.
Proof: We will use one observation that the maximum distance max d(v, w) from a given vertex v to any other vertex w occurs only when w is pendant vertex.
Now, let T is a tree with n vertices (n>=2)
T must have at least two pendant vertices. Delete all pendant vertices from T, then resulting graph T’ is still a tree. Again delete pendant vertices from T’ so that resulting T” is still a tree with same centers.
Note that all vertices that T had as centers will still remain centers in T’–>T”–>T”’–>….
continue this process until the remaining tree has either one vertex or one edge. So in the end, if one vertex is there this implies tree T has one center. If one edge is there then tree T has two centers.
- Theorem 9: Prove the maximum number of vertices at level ‘L’ in a binary tree is
 , where L>=0.
Proof: The given theorem is proved with the help of mathematical induction. At level 0 (L=0), there is only one vertex at level (L=1), there is only
, where L>=0.
Proof: The given theorem is proved with the help of mathematical induction. At level 0 (L=0), there is only one vertex at level (L=1), there is only 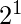 vertices.
Now we assume that statement is true for the level (L-1).
Therefore, maximum number of vertices on the level (L-1) is
vertices.
Now we assume that statement is true for the level (L-1).
Therefore, maximum number of vertices on the level (L-1) is 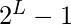 . Since we know that each vertex in a binary tree has the maximum of 2 vertices in next level, therefore the number of vertices on the level L is twice that of the level L-1.
Hence at level L, the number of vertices is:-
. Since we know that each vertex in a binary tree has the maximum of 2 vertices in next level, therefore the number of vertices on the level L is twice that of the level L-1.
Hence at level L, the number of vertices is:-
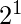 *
*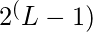 =
=  .
.
Share your thoughts in the comments
Please Login to comment...