Smallest N digit number divisible by N
Last Updated :
22 Feb, 2023
Given a positive integers N, the task is to find the smallest N digit number divisible by N.
Examples:
Input: N = 2
Output: 10
Explanation:
10 is the smallest 2-digit number which is divisible by 2.
Input: N = 3
Output: 102
Explanation:
102 is the smallest 3-digit number which is divisible by 3.
Naive Approach: The naive approach is to iterate from smallest N-digit number(say S) to largest N-digit number(say L). The first number between [S, L] divisible by N is the required result.
Below is the implementation of above approach:
C++
#include <iostream>
#include <math.h>
using namespace std;
void smallestNumber(int N)
{
int L = pow(10, N) - 1;
int S = pow(10, N - 1);
for (int i = S; i <= L; i++) {
if (i % N == 0) {
cout << i;
return;
}
}
}
int main()
{
int N = 2;
smallestNumber(N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void smallestNumber(int N)
{
int L = (int) (Math.pow(10, N) - 1);
int S = (int) Math.pow(10, N - 1);
for (int i = S; i <= L; i++)
{
if (i % N == 0)
{
System.out.print(i);
return;
}
}
}
public static void main(String[] args)
{
int N = 2;
smallestNumber(N);
}
}
|
Python3
def smallestNumber(N):
L = pow(10, N) - 1;
S = pow(10, N - 1);
for i in range(S, L):
if (i % N == 0):
print(i);
return;
if __name__ == "__main__" :
N = 2;
smallestNumber(N)
|
C#
using System;
class GFG{
static void smallestNumber(int N)
{
int L = (int)(Math.Pow(10, N) - 1);
int S = (int)Math.Pow(10, N - 1);
for(int i = S; i <= L; i++)
{
if (i % N == 0)
{
Console.Write(i);
return;
}
}
}
public static void Main()
{
int N = 2;
smallestNumber(N);
}
}
|
Javascript
<script>
function smallestNumber(N)
{
let L = Math.pow(10, N) - 1;
let S = Math.pow(10, N - 1);
for(let i = S; i <= L; i++)
{
if (i % N == 0)
{
document.write(i);
return;
}
}
}
let N = 2;
smallestNumber(N);
</script>
|
Time Complexity: O(L – S), where L and S is the largest and smallest N-digit number respectively.
Auxiliary Space: O(1)
Efficient Approach: If the number divisible by N, then the number will be of the form N * X for some positive integer X.
Since it has to be smallest N-digit number, then X will be given by:
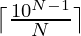 . Therefore, the smallest number N-digit number is given by:
. Therefore, the smallest number N-digit number is given by:
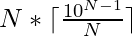
For Example:
For N = 3, the smallest 3-digit number is given by:
=> 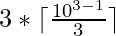
=> 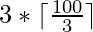
=> 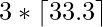
=> 102
Below is the implementation of the above approach:
C++
#include <iostream>
#include <math.h>
using namespace std;
int smallestNumber(int N)
{
return N * ceil(pow(10, (N - 1)) / N);
}
int main()
{
int N = 2;
cout << smallestNumber(N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int smallestNumber(int N)
{
return (int) (N * Math.ceil(Math.pow(10, (N - 1)) / N));
}
public static void main(String[] args)
{
int N = 2;
System.out.print(smallestNumber(N));
}
}
|
Python3
import math
def smallestNumber(N):
return N * math.ceil(pow(10, (N - 1)) // N);
N = 2;
print(smallestNumber(N));
|
C#
using System;
class GFG{
static int smallestNumber(int N)
{
return (int) (N * Math.Ceiling(Math.Pow(10, (N - 1)) / N));
}
public static void Main()
{
int N = 2;
Console.Write(smallestNumber(N));
}
}
|
Javascript
<script>
function smallestNumber(N)
{
return N * Math.ceil(Math.pow(10, (N - 1)) / N);
}
let N = 2;
document.write(smallestNumber(N));
</script>
|
Time Complexity: O(log(N))
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...