Sliding Window Maximum (Maximum of all subarrays of size K)
Last Updated :
11 Mar, 2024
Given an array and an integer K, find the maximum for each and every contiguous subarray of size K.
Examples :
Input: arr[] = {1, 2, 3, 1, 4, 5, 2, 3, 6}, K = 3
Output: 3 3 4 5 5 5 6
Explanation: Maximum of 1, 2, 3 is 3
Maximum of 2, 3, 1 is 3
Maximum of 3, 1, 4 is 4
Maximum of 1, 4, 5 is 5
Maximum of 4, 5, 2 is 5
Maximum of 5, 2, 3 is 5
Maximum of 2, 3, 6 is 6
Input: arr[] = {8, 5, 10, 7, 9, 4, 15, 12, 90, 13}, K = 4
Output: 10 10 10 15 15 90 90
Explanation: Maximum of first 4 elements is 10, similarly for next 4
elements (i.e from index 1 to 4) is 10, So the sequence
generated is 10 10 10 15 15 90 90
Naive Approach:
The idea is very basic run a nested loop, the outer loop which will mark the starting point of the subarray of length K, the inner loop will run from the starting index to index+K, and print the maximum element among these K elements.
Follow the given steps to solve the problem:
- Create a nested loop, the outer loop from starting index to N – Kth elements. The inner loop will run for K iterations.
- Create a variable to store the maximum of K elements traversed by the inner loop.
- Find the maximum of K elements traversed by the inner loop.
- Print the maximum element in every iteration of the outer loop
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void printKMax(int arr[], int N, int K)
{
int j, max;
for (int i = 0; i <= N - K; i++) {
max = arr[i];
for (j = 1; j < K; j++) {
if (arr[i + j] > max)
max = arr[i + j];
}
cout << max << " ";
}
}
int main()
{
int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
int N = sizeof(arr) / sizeof(arr[0]);
int K = 3;
printKMax(arr, N, K);
return 0;
}
|
C
#include <stdio.h>
void printKMax(int arr[], int N, int K)
{
int j, max;
for (int i = 0; i <= N - K; i++) {
max = arr[i];
for (j = 1; j < K; j++) {
if (arr[i + j] > max)
max = arr[i + j];
}
printf("%d ", max);
}
}
int main()
{
int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
int N = sizeof(arr) / sizeof(arr[0]);
int K = 3;
printKMax(arr, N, K);
return 0;
}
|
Java
public class GFG {
static void printKMax(int arr[], int N, int K)
{
int j, max;
for (int i = 0; i <= N - K; i++) {
max = arr[i];
for (j = 1; j < K; j++) {
if (arr[i + j] > max)
max = arr[i + j];
}
System.out.print(max + " ");
}
}
public static void main(String args[])
{
int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
int K = 3;
printKMax(arr, arr.length, K);
}
}
|
C#
using System;
class GFG {
static void printKMax(int[] arr, int N, int K)
{
int j, max;
for (int i = 0; i <= N - K; i++) {
max = arr[i];
for (j = 1; j < K; j++) {
if (arr[i + j] > max)
max = arr[i + j];
}
Console.Write(max + " ");
}
}
public static void Main()
{
int[] arr = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
int K = 3;
printKMax(arr, arr.Length, K);
}
}
|
Javascript
function printKMax(arr,n,k)
{
let j, max;
for (let i = 0; i <= n - k; i++)
{
max = arr[i];
for (j = 1; j < k; j++)
{
if (arr[i + j] > max)
max = arr[i + j];
}
document.write( max + " ");
}
}
let arr = [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ];
let n =arr.length;
let k = 3;
printKMax(arr, n, k);
|
PHP
<?php
function printKMax($arr, $N, $K)
{
$j; $max;
for ($i = 0; $i <= $N - $K; $i++)
{
$max = $arr[$i];
for ($j = 1; $j < $K; $j++)
{
if ($arr[$i + $j] > $max)
$max = $arr[$i + $j];
}
printf("%d ", $max);
}
}
$arr = array(1, 2, 3, 4, 5,
6, 7, 8, 9, 10);
$N = count($arr);
$K = 3;
printKMax($arr, $N, $K);
?>
|
Python3
def printMax(arr, N, K):
max = 0
for i in range(N - K + 1):
max = arr[i]
for j in range(1, K):
if arr[i + j] > max:
max = arr[i + j]
print(str(max) + " ", end="")
if __name__ == "__main__":
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
N = len(arr)
K = 3
printMax(arr, N, K)
|
Time Complexity: O(N * K), The outer loop runs N-K+1 times and the inner loop runs K times for every iteration of the outer loop. So time complexity is O((n-k+1)*k) which can also be written as O(N * K)
Auxiliary Space: O(1)
Maximum of all subarrays of size K using Max-Heap:
- Initialize an empty priority queue heap to store elements in decreasing order of their values, along with their indices.
- Push the first k elements of the input array arr into the priority queue heap along with their respective indices.
- The maximum element in the first window is obtained by accessing the top element of the priority queue heap. Push this maximum element into the answer vector ans.
- Process the remaining elements of arr starting from index k:
- Add the current element along with its index to the priority queue heap.
- Remove elements from the priority queue heap that are outside the current window. This is done by comparing the index of the top element in the heap with the index i – k. If the index of the top element is less than or equal to i – k, it means the element is outside the current window and should be removed.
- The maximum element in the current window is obtained by accessing the top element of the priority queue heap. Push this maximum element into the answer vector ans.
- Finally, return the answer vector ans containing the maximum elements in each sliding window.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<int> maxSlidingWindow(vector<int>& arr, int k)
{
vector<int> ans;
priority_queue<pair<int, int> > heap;
for (int i = 0; i < k; i++)
heap.push({ arr[i], i });
ans.push_back(heap.top().first);
for (int i = k; i < arr.size(); i++) {
heap.push({ arr[i], i });
while (heap.top().second <= i - k)
heap.pop();
ans.push_back(heap.top().first);
}
return ans;
}
int main()
{
vector<int> arr = { 2, 3, 7, 9, 5, 1, 6, 4, 3 };
int k = 3;
vector<int> result = maxSlidingWindow(arr, k);
for (auto i : result)
cout << i << " ";
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.List;
import java.util.PriorityQueue;
public class Main {
public static List<Integer> maxSlidingWindow(int[] arr,
int k)
{
List<Integer> ans = new ArrayList<>();
PriorityQueue<Pair> heap = new PriorityQueue<>(
(a, b) -> b.value - a.value);
for (int i = 0; i < k; i++) {
heap.offer(new Pair(arr[i], i));
}
ans.add(heap.peek().value);
for (int i = k; i < arr.length; i++) {
heap.offer(new Pair(arr[i], i));
while (heap.peek().index <= i - k) {
heap.poll();
}
ans.add(heap.peek().value);
}
return ans;
}
static class Pair {
int value;
int index;
public Pair(int value, int index)
{
this.value = value;
this.index = index;
}
}
public static void main(String[] args)
{
int[] arr = { 2, 3, 7, 9, 5, 1, 6, 4, 3 };
int k = 3;
List<Integer> result = maxSlidingWindow(arr, k);
for (int num : result) {
System.out.print(num + " ");
}
}
}
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static List<int> MaxSlidingWindow(List<int> arr, int k)
{
List<int> ans = new List<int>();
Queue<int> deque = new Queue<int>();
for (int i = 0; i < arr.Count; i++)
{
while (deque.Count > 0 && deque.Peek() < i - k + 1)
deque.Dequeue();
while (deque.Count > 0 && arr[deque.Peek()] < arr[i])
deque.Dequeue();
deque.Enqueue(i);
if (i >= k - 1)
ans.Add(arr[deque.Peek()]);
}
return ans;
}
static void Main()
{
List<int> arr = new List<int> { 2, 3, 7, 9, 5, 1, 6, 4, 3 };
int k = 3;
List<int> result = MaxSlidingWindow(arr, k);
foreach (int i in result)
Console.Write(i + " ");
Console.ReadLine();
}
}
|
Javascript
class Pair {
constructor(value, index) {
this.value = value;
this.index = index;
}
}
function maxSlidingWindow(arr, k) {
const ans = [];
const heap = [];
for (let i = 0; i < k; i++) {
heap.push(new Pair(arr[i], i));
}
heap.sort((a, b) => b.value - a.value);
ans.push(heap[0].value);
for (let i = k; i < arr.length; i++) {
heap.push(new Pair(arr[i], i));
while (heap[0].index <= i - k) {
heap.shift();
}
heap.sort((a, b) => b.value - a.value);
ans.push(heap[0].value);
}
return ans;
}
const arr = [2, 3, 7, 9, 5, 1, 6, 4, 3];
const k = 3;
const result = maxSlidingWindow(arr, k);
for (const num of result) {
console.log(num + " ");
}
|
Python3
import heapq
def max_sliding_window(arr, k):
ans = []
heap = []
for i in range(k):
heapq.heappush(heap, (-arr[i], i))
ans.append(-heap[0][0])
for i in range(k, len(arr)):
heapq.heappush(heap, (-arr[i], i))
while heap[0][1] <= i - k:
heapq.heappop(heap)
ans.append(-heap[0][0])
return ans
arr = [2, 3, 7, 9, 5, 1, 6, 4, 3]
k = 3
result = max_sliding_window(arr, k)
for num in result:
print(num, end=" ")
|
Time Complexity: O(NlogN), Where N is the size of the array.
Auxiliary Space: O(N), where N is the size of the array, this method requires O(N) space in the worst case when the input array is an increasing array
Maximum of all subarrays of size K using Set:
To reduce the auxilary space to O(K), Set Data Structure can be used which allows deletion of any element in O(logn N) time. Thus the size of set will never exceed K, if we delete delete the (i-Kt)h element from the Set while traversing.
Follow the given steps to solve the problem:
- Create a Set to store and find the maximum element.
- Traverse through the array from start to end.
- Insert the element in theSet.
- If the loop counter is greater than or equal to k then delete the i-Kth element from the Set.
- Print the maximum element of the Set.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<int> maxSlidingWindow(vector<int>& arr, int k)
{
vector<int> ans;
set<pair<int, int>, greater<pair<int,int>>> st;
for (int i = 0; i < k; i++)
st.insert({ arr[i], i });
ans.push_back((st.begin())->first);
for (int i = k; i < arr.size(); i++) {
st.insert({ arr[i], i });
st.erase({ arr[i - k], (i - k) });
ans.push_back(st.begin()->first);
}
return ans;
}
int main()
{
vector<int> arr = { 2, 3, 7, 9, 5, 1, 6, 4, 3 };
int k = 3;
vector<int> result = maxSlidingWindow(arr, k);
for (auto i : result)
cout << i << " ";
return 0;
}
|
Java
import java.util.ArrayDeque;
import java.util.Deque;
public class MaxSlidingWindow {
static int[] maxSlidingWindow(int[] arr, int k)
{
int n = arr.length;
int[] ans = new int[n - k + 1];
Deque<Integer> maxInWindow = new ArrayDeque<>();
for (int i = 0; i < k; i++) {
while (!maxInWindow.isEmpty()
&& arr[i]
>= arr[maxInWindow.peekLast()]) {
maxInWindow.removeLast();
}
maxInWindow.addLast(i);
}
ans[0] = arr[maxInWindow.peekFirst()];
for (int i = k; i < n; i++) {
while (!maxInWindow.isEmpty()
&& maxInWindow.peekFirst() <= i - k) {
maxInWindow.removeFirst();
}
while (!maxInWindow.isEmpty()
&& arr[i]
>= arr[maxInWindow.peekLast()]) {
maxInWindow.removeLast();
}
maxInWindow.addLast(i);
ans[i - k + 1] = arr[maxInWindow.peekFirst()];
}
return ans;
}
public static void main(String[] args)
{
int[] arr = { 2, 3, 7, 9, 5, 1, 6, 4, 3 };
int k = 3;
int[] result = maxSlidingWindow(arr, k);
System.out.print(
"Maximum elements in each sliding window: ");
for (int i : result)
System.out.print(i + " ");
}
}
|
Python
from collections import deque
def maxSlidingWindow(arr, k):
ans = []
deq = deque()
for i in range(k):
while deq and arr[i] >= arr[deq[-1]]:
deq.pop()
deq.append(i)
ans.append(arr[deq[0]])
for i in range(k, len(arr)):
while deq and deq[0] <= i - k:
deq.popleft()
while deq and arr[i] >= arr[deq[-1]]:
deq.pop()
deq.append(i)
ans.append(arr[deq[0]])
return ans
if __name__ == "__main__":
arr = [2, 3, 7, 9, 5, 1, 6, 4, 3]
k = 3
result = maxSlidingWindow(arr, k)
print(result)
|
C#
using System;
using System.Collections.Generic;
class Program {
static List<int> MaxSlidingWindow(List<int> arr, int k)
{
List<int> ans = new List<int>();
List<int> maxInWindow = new List<int>();
for (int i = 0; i < k; i++) {
while (
maxInWindow.Count > 0
&& arr[i]
>= arr[maxInWindow[maxInWindow.Count
- 1]]) {
maxInWindow.RemoveAt(maxInWindow.Count - 1);
}
maxInWindow.Add(i);
}
ans.Add(arr[maxInWindow[0]]);
for (int i = k; i < arr.Count; i++) {
while (maxInWindow.Count > 0
&& maxInWindow[0] <= i - k) {
maxInWindow.RemoveAt(0);
}
while (
maxInWindow.Count > 0
&& arr[i]
>= arr[maxInWindow[maxInWindow.Count
- 1]]) {
maxInWindow.RemoveAt(maxInWindow.Count - 1);
}
maxInWindow.Add(i);
ans.Add(arr[maxInWindow[0]]);
}
return ans;
}
static void Main(string[] args)
{
List<int> arr
= new List<int>{ 2, 3, 7, 9, 5, 1, 6, 4, 3 };
int k = 3;
List<int> result = MaxSlidingWindow(arr, k);
Console.WriteLine(
"Maximum elements in each sliding window:");
foreach(int i in result) { Console.Write(i + " "); }
}
}
|
Javascript
function maxSlidingWindow(arr, k) {
const ans = [];
const maxInWindow = [];
for (let i = 0; i < k; i++) {
while (maxInWindow.length > 0 && arr[i] >= arr[maxInWindow[maxInWindow.length - 1]]) {
maxInWindow.pop();
}
maxInWindow.push(i);
}
ans.push(arr[maxInWindow[0]]);
for (let i = k; i < arr.length; i++) {
while (maxInWindow.length > 0 && maxInWindow[0] <= i - k) {
maxInWindow.shift();
}
while (maxInWindow.length > 0 && arr[i] >= arr[maxInWindow[maxInWindow.length - 1]]) {
maxInWindow.pop();
}
maxInWindow.push(i);
ans.push(arr[maxInWindow[0]]);
}
return ans;
}
const arr = [2, 3, 7, 9, 5, 1, 6, 4, 3];
const k = 3;
const result = maxSlidingWindow(arr, k);
console.log("Maximum elements in each sliding window: " + result.join(' '));
|
Time Complexity: O(NlogN), Where N is the size of the array.
Auxiliary Space: O(K), since size of set does not never exceeds K.
Maximum of all subarrays of size K using Deque:
Create a Deque, Qi of capacity K, that stores only useful elements of current window of K elements. An element is useful if it is in current window and is greater than all other elements on right side of it in current window. Process all array elements one by one and maintain Qi to contain useful elements of current window and these useful elements are maintained in sorted order. The element at front of the Qi is the largest and element at rear/back of Qi is the smallest of current window.
Below is the dry run of the above approach:
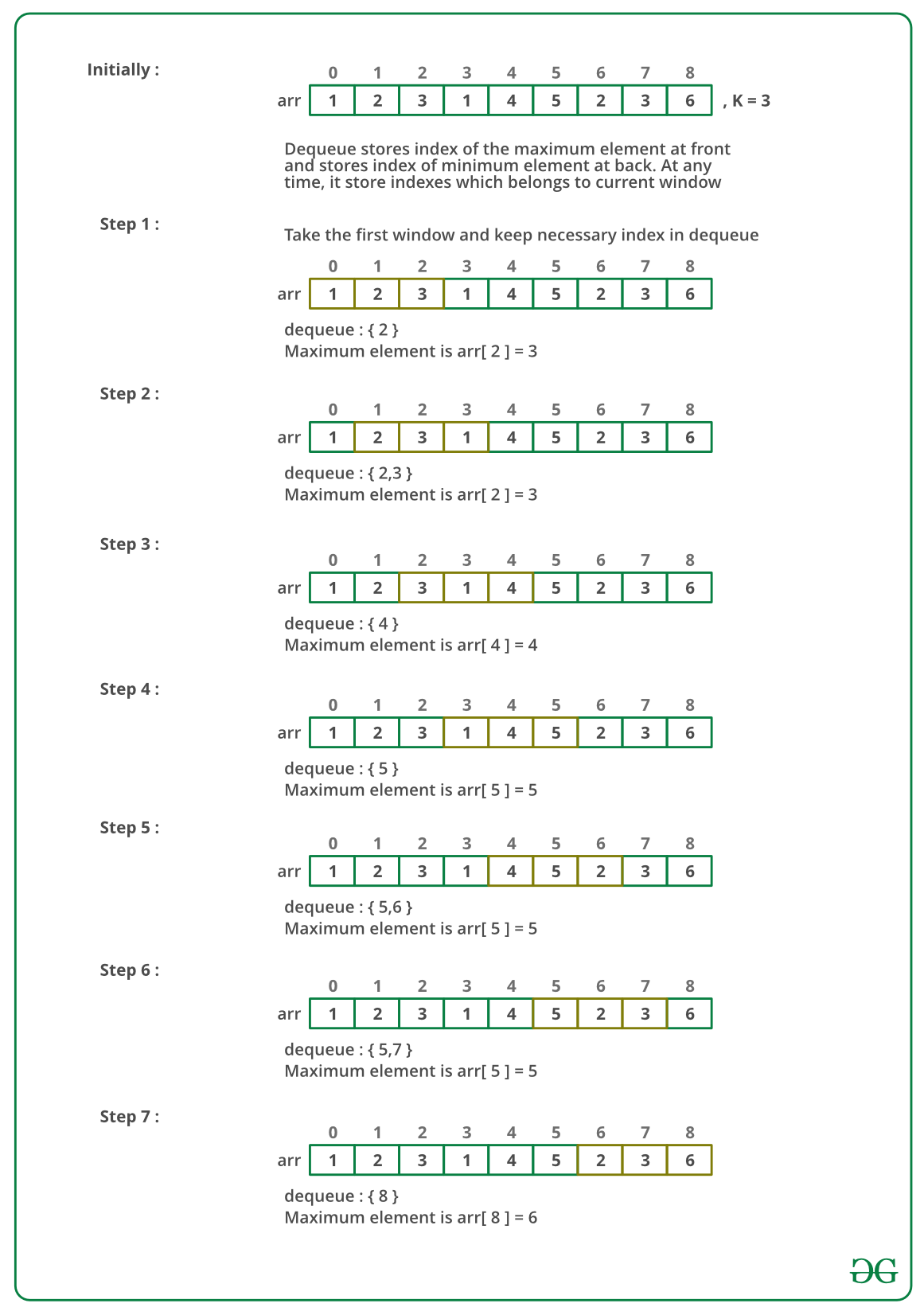
Follow the given steps to solve the problem:
- Create a deque to store K elements.
- Run a loop and insert the first K elements in the deque. Before inserting the element, check if the element at the back of the queue is smaller than the current element, if it is so remove the element from the back of the deque until all elements left in the deque are greater than the current element. Then insert the current element, at the back of the deque.
- Now, run a loop from K to the end of the array.
- Print the front element of the deque.
- Remove the element from the front of the queue if they are out of the current window.
- Insert the next element in the deque. Before inserting the element, check if the element at the back of the queue is smaller than the current element, if it is so remove the element from the back of the deque until all elements left in the deque are greater than the current element. Then insert the current element, at the back of the deque.
- Print the maximum element of the last window.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void printKMax(int arr[], int N, int K)
{
std::deque<int> Qi(K);
int i;
for (i = 0; i < K; ++i) {
while ((!Qi.empty()) && arr[i] >= arr[Qi.back()])
Qi.pop_back();
Qi.push_back(i);
}
for (; i < N; ++i) {
cout << arr[Qi.front()] << " ";
while ((!Qi.empty()) && Qi.front() <= i - K)
Qi.pop_front();
while ((!Qi.empty()) && arr[i] >= arr[Qi.back()])
Qi.pop_back();
Qi.push_back(i);
}
cout << arr[Qi.front()];
}
int main()
{
int arr[] = { 12, 1, 78, 90, 57, 89, 56 };
int N = sizeof(arr) / sizeof(arr[0]);
int K = 3;
printKMax(arr, N, K);
return 0;
}
|
Java
import java.util.Deque;
import java.util.LinkedList;
public class SlidingWindow {
static void printMax(int arr[], int N, int K)
{
Deque<Integer> Qi = new LinkedList<Integer>();
int i;
for (i = 0; i < K; ++i) {
while (!Qi.isEmpty()
&& arr[i] >= arr[Qi.peekLast()])
Qi.removeLast();
Qi.addLast(i);
}
for (; i < N; ++i) {
System.out.print(arr[Qi.peek()] + " ");
while ((!Qi.isEmpty()) && Qi.peek() <= i - K)
Qi.removeFirst();
while ((!Qi.isEmpty())
&& arr[i] >= arr[Qi.peekLast()])
Qi.removeLast();
Qi.addLast(i);
}
System.out.print(arr[Qi.peek()]);
}
public static void main(String[] args)
{
int arr[] = { 12, 1, 78, 90, 57, 89, 56 };
int K = 3;
printMax(arr, arr.length, K);
}
}
|
C#
using System;
using System.Collections.Generic;
public class SlidingWindow {
static void printMax(int[] arr, int N, int K)
{
List<int> Qi = new List<int>();
int i;
for (i = 0; i < K; ++i) {
while (Qi.Count != 0
&& arr[i] >= arr[Qi[Qi.Count - 1]])
Qi.RemoveAt(Qi.Count - 1);
Qi.Insert(Qi.Count, i);
}
for (; i < N; ++i) {
Console.Write(arr[Qi[0]] + " ");
while ((Qi.Count != 0) && Qi[0] <= i - K)
Qi.RemoveAt(0);
while ((Qi.Count != 0)
&& arr[i] >= arr[Qi[Qi.Count - 1]])
Qi.RemoveAt(Qi.Count - 1);
Qi.Insert(Qi.Count, i);
}
Console.Write(arr[Qi[0]]);
}
public static void Main(String[] args)
{
int[] arr = { 12, 1, 78, 90, 57, 89, 56 };
int K = 3;
printMax(arr, arr.Length, K);
}
}
|
Javascript
function printKMax(arr,n,k)
{
let str ="";
let Qi = [];
let i;
for (i = 0; i < k; ++i)
{
while ((Qi.length!=0) && arr[i] >=
arr[Qi[Qi.length-1]])
Qi.pop();
Qi.push(i);
}
for (i; i < n; ++i)
{
str+=arr[Qi[0]] + " ";
while ((Qi.length!=0) && Qi[0] <= i - k)
Qi.shift();
while ((Qi.length!=0) && arr[i] >= arr[Qi[Qi.length-1]])
Qi.pop();
Qi.push(i);
}
str += arr[Qi[0]];
console.log(str);
}
let arr = [ 12, 1, 78, 90, 57, 89, 56 ];
let n = arr.length;
let k = 3;
printKMax(arr, n, k);
|
Python3
from collections import deque
def printMax(arr, N, K):
Qi = deque()
for i in range(K):
while Qi and arr[i] >= arr[Qi[-1]]:
Qi.pop()
Qi.append(i)
for i in range(K, N):
print(str(arr[Qi[0]]) + " ", end="")
while Qi and Qi[0] <= i-K:
Qi.popleft()
while Qi and arr[i] >= arr[Qi[-1]]:
Qi.pop()
Qi.append(i)
print(str(arr[Qi[0]]))
if __name__ == "__main__":
arr = [12, 1, 78, 90, 57, 89, 56]
K = 3
printMax(arr, len(arr), K)
|
Time Complexity: O(N). It seems more than O(N) at first look. It can be observed that every element of the array is added and removed at most once. So there are a total of 2n operations.
Auxiliary Space: O(K). Elements stored in the dequeue take O(K) space.
Below is an extension of this problem:
Sum of minimum and maximum elements of all subarrays of size k.
Share your thoughts in the comments
Please Login to comment...