Signum Function

Signum Function is an important function in mathematics that helps us to know the sign of a real number. It is usually expressed as a function of a variable and denoted either by f(x) or by sgn(x). It may also be written as a sign(x). Signum Function also has applications in various fields such as physics, electronics, and AI due to which it becomes much more important to study signum function.

Signum Function

A signum function is neither a one-one nor an onto function as various elements has the same image and a pre-image has various images in the co-domain and domain set respectively. In this article, we shall discuss the signum function in detail.

What is Signum Function?

Signum function is a special type of function in Mathematics that attributes +1 (positive one) and -1(negative one) for the positive, and negative values of the input. This means that if a positive value is supplied to the signum function, the output is always +1, and it is -1 if a negative value is supplied to the signum function. In the case of zero, the output is always zero. 

Signum Function Definition

The signum function is mathematically defined as follows:

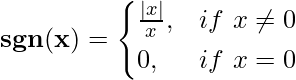
This function can be written in simplified form as follows:

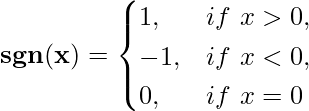
Domain and Range of Signum Function

The Domain of the signum function is all real numbers i.e. R and the co-domain and range of the signum function are [-1, 0, 1].

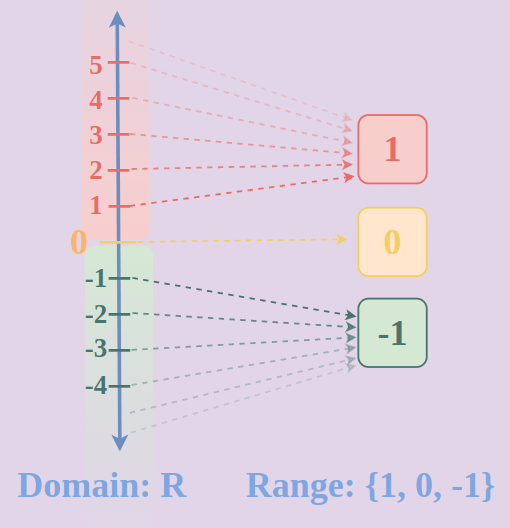
Signum Function Graph

The graph for the signum function has three components. It is a straight line parallel to the X-axis with a y-intercept of 1 for all positive values. The graph is a straight line parallel to X-axis intersecting Y axis at -1 whereas for 0 it is a simple point with coordinates (0, 0) i.e. origin. The graph for the signum function is shown below:

Properties of Signum Function

Signum function sgn(x) has the following properties:

• If sgn(x) = 1, x>0
• If sgn(x) = -1, x<0
• x = |x|sgn(x)
• sgn(x.y) = sgn(x).sgn(y)
• sgn(sgn(x)) = sgn(x)
• sgn(x+y) < sgn(x) + sgn(y) + 1
• If x≠0, then sgn(x)sgn(1/x) = 1
• If x≠0, then sgn(1/x) = 1/sgn(x)
• sgn(x)+sgn(y)-1 ≤ sgn(x+y)
• If x≠0, then sgn(x)=sgn(1/x)
• If y≠0, then sgn(x/y)=sgn(x)/sgn(y)

Applications of Signum Function

Signum function has various applications in different fields. Some of its applications are:

• It is used to find the sign of the real number
• It helps to project a complex number on the unit circle
• A positively or negatively inclined line with the X-axis is obtained when the signum function is integrated
• It can also be used to predict the probability of the occurrence of an event.
• It is also used for implementing the on and off switch in electronic devices.
• It also finds applications in a thermostat such that the system starts cooling above a specific temperature and stops cooling below a specific temperature.

Solved Problems on Signum Function

Problem 1: Find the probable values of x if sgn(x² – 5x + 6) = 1.

Answer:

We know that the signum function gives a value of 1 when the value supplied to it is greater than 0.

Thus x² – 5x + 6 > 0

(x-3)(x-2) > 0

It is only possible if both (x-2) and (x-3) are either positive or negative.

Case 1: If both are positive

x can assume the values greater than 3 i.e. x ∈ (3, ∞)

Case 2: If both are negative

x can assume the values lesser than 2 i.e. x ∈ (-∞, 2)

Thus the probable values of x are (-∞, 2) U (3, ∞).

Problem 2: Find the probable values of x if sgn(2x² – 7x + 6) = 1.

Answer:

We know that the signum function gives a value of 1 when the value supplied to it is greater than 0.

Thus 2x² – 7x + 6 > 0

(2x-3)(x-2) > 0

It is only possible if both (x-2) and (2x-3) are either positive or negative.

Case 1: If both are positive

x can assume the values greater than 2 i.e. x ∈ (2, ∞)

Case 2: If both are negative

x can assume the values lesser than 3/2 i.e. x ∈ (-∞, 3/2)

Thus the probable values of x are (-∞, 3/2) U (2, ∞).

Problem 3: Calculate the value of the signum function for the values in the set [1, -0.5, 0.435, 0].

Answer:

We know that 

Thus sgn(1) = 1,sgn(-0.5) = -1,

sgn(0.435) = 1, and

sgn(0) = 0

Problem 4: Calculate the value of sgn(1/x) if sgn(x) = -1.

Answer:

As, sgn(x)sgn(1/x) = 1 if x is not equal to zero.

Thus sgn(1/x)(-1) = 1

Therefore, sgn(1/x) = -1

Signum Function – FAQs

Define Signum Function?

A signum function is a special type of function which returns +1 for all values greater than zero, -1 for all values lesser than 0 and zero if the value is equal to zero.

Is Signum Function An Even Function Or an Odd Function?

Signum function is an odd function as sgn(x) = -sgn(-x).

Give Two Applications Of Signum Function.

Applications of signum function are:

• It helps to project a complex number on unit circle
• It is also used for implementing the on and off switched in electronic devices.

What Will Be the Graph of Signum Function For x=0.5?

As sgn(0.5) = 1. Thus graph of signum function in this case will be a straight line parallel to X-axis intersecting Y-axis at y=1.

What Is The Domain And Range Of Signum Function?

The domain of signum function is all real numbers which is represented by R and the range of signum function is the set [-1, 0, 1].