Sheppard’s Correction for Moments | ML
Last Updated :
23 Jan, 2020
Prerequisite: Raw and Central Moments
We assume in grouped data that the frequencies are concentrated in the middle part of the class interval. This assumption does not hold true in general and
grouping error is introduced. Such an effect can be corrected in calculating the moments by using the information on the width of the class interval.
Sheppard’s Correction for grouping error is nothing but the adjustment to calculated sample moments for the grouped data or continuous data. Prof. W.F. Sheppard proved that if the frequency distribution is continuous and the frequency tapers off to zero in both directions, the grouping error can be corrected as follows:
Let
‘c’ be the width of the class interval. Then,
Raw Moments
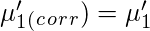
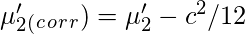
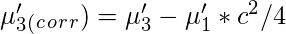
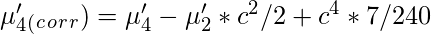 Central Moments
Central Moments
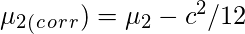
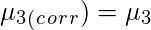
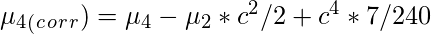 What Kind of data can be corrected?
What Kind of data can be corrected?
- This method of correction to moments is only possible for the continuous variables i.e. the continuous data.
- The width of the class interval should be equal.
- Frequencies should be symmetrical. Frequency should taper off to zero in both directions.
Consider the given distribution of marks.
| Marks |
Number of Students |
| 0 – 10 |
1 |
| 10 – 20 |
6 |
| 20 – 30 |
11 |
| 30 – 40 |
17 |
| 40 – 50 |
21 |
| 50 – 60 |
16 |
| 60 – 70 |
13 |
| 70 – 80 |
7 |
| 80 – 90 |
5 |
| 90 – 100 |
2 |
For the distribution of marks above, the value for moments are given below:
Raw Moments –
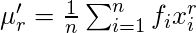
, is the rth raw moment, where
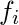
is the frequency count and
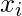
is the mid value of class.
So, using the above formula for the
Raw Moment we get following values for moments.
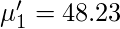
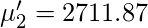
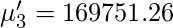
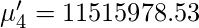 Sheppard’s correction for Raw Moments –
Sheppard’s correction for Raw Moments –
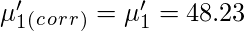
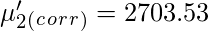
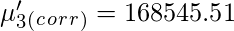
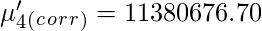
Similarly central moments can be corrected using
Sheppard’s Correction.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...