Bessel’s correction

Bessel correction refers to the n-1 part used as the denominator in the formula of sample variance or sample distribution.

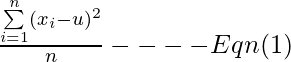
Why n-1? Suppose n independent observations are drawn from a population with mean(u) and variance(sigma²). In general both (u) and (sigma) are unknown and are to be estimated.  The sample-mean, estimates the population-mean(u) and the sample-variance s² estimates the population variance (sigma²). Ideally (sigma²) should be estimated with Since u is not known so sample-mean proves to be the best estimator that can be used. Hence 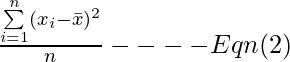Problem: Subtracting sample-mean in Eqn(2) makes this sum as small as it possibly could be, roughly the sample mean must fall near the center of the observations whereas population-mean could be any value. So the sum in Eqn(2) is going to be smaller than the sum in the Eqn(1), hence Eqn(2) tends to underestimate the true value of the population variance. Solution: To compensate for that, dividing by n-1 makes the sample variance a little bigger than it would be if divide by n. It turns out that mathematically it properly compensates for the problem. 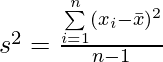On average this estimator equals the population variance(sigma²), it’s not obvious here why here (n-1) works, why this estimator on an average equals the population variance(sigma²)? Why is (n-2) or (n-3) or (n-0.5) not used for the division?

When the sample standard deviation is calculated from a sample of n values, sample mean is used which has already been calculated from that same sample of n values. The calculated sample mean has already “used up” one of the “degrees of freedom of variability”(which is the mean itself) that is available in the sample. Only n-1 degrees of freedom of variability are left for the calculation of the sample standard deviation. 

Example: Suppose 3 independent observations are drawn from a population where population-mean(u) is unknown, we find that sample-mean=5 and we use that to estimate population-mean(u). Given this information the first two observations can be anything, suppose them to be 7 & 5.

i	xi	xi-(sample_mean)
1.	7	7-5=2
2.	5	5-5=0
3.	3	3-5=-2

If the mean of the observation is 5 and we know the first two observations to be 7 & 5 then the third must be 3 and we know this third deviation must be -2, as all the deviations from the sample mean always sum to zero. So the third observation isn’t free to be any value anymore so here only two degrees of freedom is left once the sample mean and any two of these three values are known we know what the third value must be, we started with three degrees of freedom when we had three independent observations from the population but we lost one degree of freedom when we estimated population-mean(u) with sample-mean. Hence to calculate the sample-variance(s²) here we take the sum of squared deviations and we divide it by the degrees of freedom (3-1).

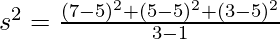
So, when estimating the population variance, it is typically divided by the degrees of freedom as opposed to the sample-size as this results in a better estimator.