Serialize and Deserialize an N-ary Tree
Last Updated :
26 Mar, 2024
Given an N-ary tree where every node has the most N children. How to serialize and deserialize it? Serialization is to store a tree in a file so that it can be later restored. The structure of the tree must be maintained. Deserialization is reading the tree back from the file.
This post is mainly an extension of the below post. Serialize and Deserialize a Binary Tree
In an N-ary tree, there are no designated left and right children. An N-ary tree is represented by storing an array or list of child pointers with every node.
The idea is to store an ‘end of children’ marker with every node. The following diagram shows serialization where ‘)’ is used as the end of the children’s marker.
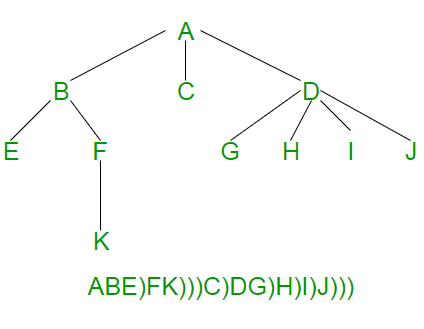
Following is the implementation of the above idea.
C++
// A C++ Program serialize and deserialize an N-ary tree
#include<cstdio>
#define MARKER ')'
#define N 5
using namespace std;
// A node of N-ary tree
struct Node {
char key;
Node *child[N]; // An array of pointers for N children
};
// A utility function to create a new N-ary tree node
Node *newNode(char key)
{
Node *temp = new Node;
temp->key = key;
for (int i = 0; i < N; i++)
temp->child[i] = NULL;
return temp;
}
// This function stores the given N-ary tree in a file pointed by fp
void serialize(Node *root, FILE *fp)
{
// Base case
if (root == NULL) return;
// Else, store current node and recur for its children
fprintf(fp, "%c ", root->key);
for (int i = 0; i < N && root->child[i]; i++)
serialize(root->child[i], fp);
// Store marker at the end of children
fprintf(fp, "%c ", MARKER);
}
// This function constructs N-ary tree from a file pointed by 'fp'.
// This function returns 0 to indicate that the next item is a valid
// tree key. Else returns 0
int deSerialize(Node *&root, FILE *fp)
{
// Read next item from file. If there are no more items or next
// item is marker, then return 1 to indicate same
char val;
if ( !fscanf(fp, "%c ", &val) || val == MARKER )
return 1;
// Else create node with this item and recur for children
root = newNode(val);
for (int i = 0; i < N; i++)
if (deSerialize(root->child[i], fp))
break;
// Finally return 0 for successful finish
return 0;
}
// A utility function to create a dummy tree shown in above diagram
Node *createDummyTree()
{
Node *root = newNode('A');
root->child[0] = newNode('B');
root->child[1] = newNode('C');
root->child[2] = newNode('D');
root->child[0]->child[0] = newNode('E');
root->child[0]->child[1] = newNode('F');
root->child[2]->child[0] = newNode('G');
root->child[2]->child[1] = newNode('H');
root->child[2]->child[2] = newNode('I');
root->child[2]->child[3] = newNode('J');
root->child[0]->child[1]->child[0] = newNode('K');
return root;
}
// A utility function to traverse the constructed N-ary tree
void traverse(Node *root)
{
if (root)
{
printf("%c ", root->key);
for (int i = 0; i < N; i++)
traverse(root->child[i]);
}
}
// Driver program to test above functions
int main()
{
// Let us create an N-ary tree shown in above diagram
Node *root = createDummyTree();
// Let us open a file and serialize the tree into the file
FILE *fp = fopen("tree.txt", "w");
if (fp == NULL)
{
puts("Could not open file");
return 0;
}
serialize(root, fp);
fclose(fp);
// Let us deserialize the stored tree into root1
Node *root1 = NULL;
fp = fopen("tree.txt", "r");
deSerialize(root1, fp);
printf("Constructed N-Ary Tree from file is \n");
traverse(root1);
return 0;
}
import java.io.*;
public class NAryTreeSerialization {
final static int N = 5;
final static char MARKER = ')';
// A node of N-ary tree
static class Node {
char key;
Node[] child; // An array of pointers for N children
Node(char key) {
this.key = key;
child = new Node[N];
}
}
// This function stores the given N-ary tree in a file pointed by fp
static void serialize(Node root, PrintWriter writer) {
// Base case
if (root == null) {
return;
}
// Else, store current node and recur for its children
writer.print(root.key + " ");
for (int i = 0; i < N && root.child[i] != null; i++) {
serialize(root.child[i], writer);
}
// Store marker at the end of children
writer.print(MARKER + " ");
}
// This function constructs N-ary tree from a file pointed by 'reader'.
static Node deSerialize(BufferedReader reader) throws IOException {
// Read next item from file. If there are no more items or next
// item is marker, then return null to indicate same
int val = reader.read();
if (val == -1 || val == MARKER) {
return null;
}
char c = (char) val;
// Else create node with this item and recur for children
Node root = new Node(c);
for (int i = 0; i < N; i++) {
root.child[i] = deSerialize(reader);
if (root.child[i] == null) {
break;
}
}
return root;
}
// A utility function to create a dummy tree shown in above diagram
static Node createDummyTree() {
Node root = new Node('A');
root.child[0] = new Node('B');
root.child[1] = new Node('C');
root.child[2] = new Node('D');
root.child[0].child[0] = new Node('E');
root.child[0].child[1] = new Node('F');
root.child[2].child[0] = new Node('G');
root.child[2].child[1] = new Node('H');
root.child[2].child[2] = new Node('I');
root.child[2].child[3] = new Node('J');
root.child[0].child[1].child[0] = new Node('K');
return root;
}
// A utility function to traverse the constructed N-ary tree
static void traverse(Node root) {
if (root != null) {
System.out.print(root.key + " ");
for (int i = 0; i < N; i++) {
traverse(root.child[i]);
}
}
}
// Driver program to test above functions
public static void main(String[] args) throws IOException {
// Let us create an N-ary tree shown in above diagram
Node root = createDummyTree();
// Let us open a file and serialize the tree into the file
PrintWriter writer = new PrintWriter(new FileWriter("tree.txt"));
serialize(root, writer);
writer.close();
// Let us deserialize the stored tree into root1
Node root1;
BufferedReader reader = new BufferedReader(new FileReader("tree.txt"));
root1 = deSerialize(reader);
reader.close();
System.out.println("Constructed N-Ary Tree from file is: ");
traverse(root1);
}
}
using System;
using System.IO;
public class GFG {
const int N = 5;
const char MARKER = ')';
// A node of N-ary tree
class Node {
public char key;
public Node[] child; // An array of pointers for N
// children
public Node(char key)
{
this.key = key;
child = new Node[N];
}
}
// This function stores the given N-ary tree in a file
// pointed by fp
static void serialize(Node root, StreamWriter writer)
{
// Base case
if (root == null) {
return;
}
// Else, store current node and recur for its
// children
writer.Write(root.key + " ");
for (int i = 0; i < N && root.child[i] != null;
i++) {
serialize(root.child[i], writer);
}
// Store marker at the end of children
writer.Write(MARKER + " ");
}
// This function constructs N-ary tree from a file
// pointed by 'reader'.
static Node deSerialize(StreamReader reader)
{
// Read next item from file. If there are no more
// items or next item is marker, then return null to
// indicate same
int val = reader.Read();
if (val == -1 || val == MARKER) {
return null;
}
char c = (char)val;
// Else create node with this item and recur for
// children
Node root = new Node(c);
for (int i = 0; i < N; i++) {
root.child[i] = deSerialize(reader);
if (root.child[i] == null) {
break;
}
}
return root;
}
// A utility function to create a dummy tree shown in
// above diagram
static Node createDummyTree()
{
Node root = new Node('A');
root.child[0] = new Node('B');
root.child[1] = new Node('C');
root.child[2] = new Node('D');
root.child[0].child[0] = new Node('E');
root.child[0].child[1] = new Node('F');
root.child[2].child[0] = new Node('G');
root.child[2].child[1] = new Node('H');
root.child[2].child[2] = new Node('I');
root.child[2].child[3] = new Node('J');
root.child[0].child[1].child[0] = new Node('K');
return root;
}
// A utility function to traverse the constructed N-ary
// tree
static void traverse(Node root)
{
if (root != null) {
Console.Write(root.key + " ");
for (int i = 0; i < N; i++) {
traverse(root.child[i]);
}
}
}
// Driver program to test above functions
static void Main(string[] args)
{
// Let us create an N-ary tree shown in above
// diagram
Node root = createDummyTree();
// Let us open a file and serialize the tree into
// the file
StreamWriter writer = new StreamWriter("tree.txt");
serialize(root, writer);
writer.Close();
// Let us deserialize the stored tree into root1
Node root1;
StreamReader reader = new StreamReader("tree.txt");
root1 = deSerialize(reader);
reader.Close();
Console.WriteLine(
"Constructed N-Ary Tree from file is: ");
traverse(root1);
}
}
// Define a class for the Node of the N-ary tree
class Node {
constructor(key) {
this.key = key;
this.children = [];
}
}
// Utility function to create a new N-ary tree node
function newNode(key) {
return new Node(key);
}
// This function stores the given N-ary tree in a string
function serialize(root) {
// Base case
if (!root) return "";
// Else, store current node and recur for its children
let serialized = root.key + " ";
for (const child of root.children) {
serialized += serialize(child);
}
// Store marker at the end of children
serialized += ") ";
return serialized;
}
// This function constructs N-ary tree from a string.
function deserialize(serialized) {
const values = serialized.split(" ");
let index = 0;
function buildTree() {
// Read next item from string. If there are no more items or next
// item is marker, then return null to indicate same
const value = values[index++];
if (!value || value === ")") return null;
// Else create node with this item and recur for children
const node = newNode(value);
while (true) {
const child = buildTree();
if (!child) break;
node.children.push(child);
}
// Finally return the node for successful finish
return node;
}
return buildTree();
}
// A utility function to create a dummy tree shown in above diagram
function createDummyTree() {
const root = newNode('A');
root.children = [newNode('B'), newNode('C'), newNode('D')];
root.children[0].children = [newNode('E'), newNode('F')];
root.children[2].children = [newNode('G'), newNode('H'), newNode('I'), newNode('J')];
root.children[0].children[1].children = [newNode('K')];
return root;
}
// A utility function to traverse the constructed N-ary tree
function traverse(root) {
if (root) {
console.log(root.key, " ");
for (const child of root.children) {
traverse(child);
}
}
}
// Driver program to test above functions
function main() {
// Let us create an N-ary tree shown in above diagram
const root = createDummyTree();
// Let us serialize the tree into a string
const serializedTree = serialize(root);
console.log("Serialized N-Ary Tree: ", serializedTree);
// Let us deserialize the stored tree into root1
const root1 = deserialize(serializedTree);
console.log("Constructed N-Ary Tree from string is ");
traverse(root1);
}
main();
# A Python program to serialize and deserialize an N-ary tree
import sys
# A node of N-ary tree
class Node:
def __init__(self, key):
self.key = key
self.children = []
# A utility function to create a new N-ary tree node
def newNode(key):
temp = Node(key)
return temp
# This function stores the given N-ary tree in a file pointed by fp
def serialize(root, fp):
# Base case
if not root:
return
# Else, store current node and recur for its children
fp.write(root.key + " ")
for child in root.children:
serialize(child, fp)
# Store marker at the end of children
fp.write(") ")
# This function constructs N-ary tree from a file pointed by 'fp'.
# This function returns 0 to indicate that the next item is a valid
# tree key. Else returns 0
def deSerialize(fp):
# Read next item from file. If there are no more items or next
# item is marker, then return None to indicate same
val = fp.read(1)
if not val or val == ")":
return None
# Else create node with this item and recur for children
root = newNode(val)
while True:
child = deSerialize(fp)
if not child:
break
root.children.append(child)
# Finally return the node for successful finish
return root
# A utility function to create a dummy tree shown in above diagram
def createDummyTree():
root = newNode('A')
root.children = [newNode('B'), newNode('C'), newNode('D')]
root.children[0].children = [newNode('E'), newNode('F')]
root.children[2].children = [newNode('G'), newNode('H'), newNode('I'), newNode('J')]
root.children[0].children[1].children = [newNode('K')]
return root
# A utility function to traverse the constructed N-ary tree
def traverse(root):
if root:
print(root.key, end=" ")
for child in root.children:
traverse(child)
# Driver program to test above functions
def main():
# Let us create an N-ary tree shown in above diagram
root = createDummyTree()
# Let us open a file and serialize the tree into the file
fp = open("tree.txt", "w")
serialize(root, fp)
fp.close()
# Let us deserialize the stored tree into root1
fp = open("tree.txt", "r")
root1 = deSerialize(fp)
fp.close()
print("Constructed N-Ary Tree from file is ")
traverse(root1)
if __name__ == '__main__':
main()
OutputConstructed N-Ary Tree from file is
A B E F K C D G H I J
Time Complexity: O(N), where n is number of nodes.
Auxiliary Space: O(H+N) , where h is height of tree and n is number of nodes.
The above implementation can be optimized in many ways for example by using a vector in place of array of pointers. We have kept it this way to keep it simple to read and understand.
Share your thoughts in the comments
Please Login to comment...