Separate Chaining Collision Handling Technique in Hashing
Last Updated :
29 Dec, 2023
What is Collision?
Since a hash function gets us a small number for a key which is a big integer or string, there is a possibility that two keys result in the same value. The situation where a newly inserted key maps to an already occupied slot in the hash table is called collision and must be handled using some collision handling technique.
What are the chances of collisions with the large table?
Collisions are very likely even if we have a big table to store keys. An important observation is Birthday Paradox. With only 23 persons, the probability that two people have the same birthday is 50%.
How to handle Collisions?
There are mainly two methods to handle collision:
- Separate Chaining
- Open Addressing
In this article, only separate chaining is discussed. We will be discussing Open addressing in the next post
Separate Chaining:
The idea behind separate chaining is to implement the array as a linked list called a chain. Separate chaining is one of the most popular and commonly used techniques in order to handle collisions.
The linked list data structure is used to implement this technique. So what happens is, when multiple elements are hashed into the same slot index, then these elements are inserted into a singly-linked list which is known as a chain.
Here, all those elements that hash into the same slot index are inserted into a linked list. Now, we can use a key K to search in the linked list by just linearly traversing. If the intrinsic key for any entry is equal to K then it means that we have found our entry. If we have reached the end of the linked list and yet we haven’t found our entry then it means that the entry does not exist. Hence, the conclusion is that in separate chaining, if two different elements have the same hash value then we store both the elements in the same linked list one after the other.
Example: Let us consider a simple hash function as “key mod 7” and a sequence of keys as 50, 700, 76, 85, 92, 73, 101
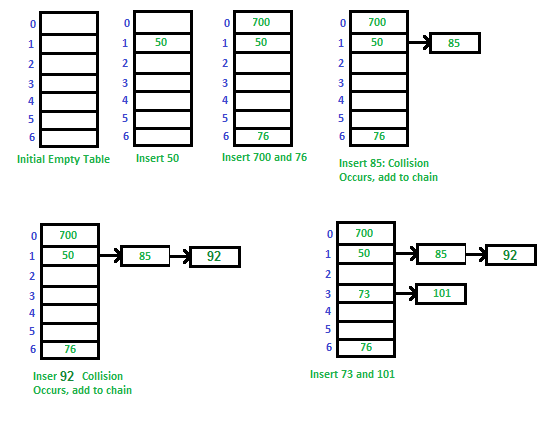
You can refer to the following link in order to understand how to implement separate chaining with C++.
C++ program for hashing with chaining
Advantages:
- Simple to implement.
- Hash table never fills up, we can always add more elements to the chain.
- Less sensitive to the hash function or load factors.
- It is mostly used when it is unknown how many and how frequently keys may be inserted or deleted.
Disadvantages:
- The cache performance of chaining is not good as keys are stored using a linked list. Open addressing provides better cache performance as everything is stored in the same table.
- Wastage of Space (Some Parts of the hash table are never used)
- If the chain becomes long, then search time can become O(n) in the worst case
- Uses extra space for links
Performance of Chaining:
Performance of hashing can be evaluated under the assumption that each key is equally likely to be hashed to any slot of the table (simple uniform hashing).
m = Number of slots in hash table
n = Number of keys to be inserted in hash table
Load factor α = n/m
Expected time to search = O(1 + α)
Expected time to delete = O(1 + α)
Time to insert = O(1)
Time complexity of search insert and delete is O(1) if α is O(1)
Data Structures For Storing Chains:
1. Linked lists
- Search: O(l) where l = length of linked list
- Delete: O(l)
- Insert: O(l)
- Not cache friendly
2. Dynamic Sized Arrays ( Vectors in C++, ArrayList in Java, list in Python)
- Search: O(l) where l = length of array
- Delete: O(l)
- Insert: O(l)
- Cache friendly
3. Self Balancing BST ( AVL Trees, Red-Black Trees)
- Search: O(log(l)) where l = length of linked list
- Delete: O(log(l))
- Insert: O(log(i))
- Not cache friendly
- Java 8 onwards use this for HashMap
Related Post: Hashing | Set 1 (Introduction)
Next Post:
Open Addressing for Collision Handling
Share your thoughts in the comments
Please Login to comment...