Birthday Paradox
Last Updated :
19 May, 2023
How many people must be there in a room to make the probability 100% that at-least two people in the room have same birthday?
Answer: 367 (since there are 366 possible birthdays, including February 29).
The above question was simple. Try the below question yourself.
How many people must be there in a room to make the probability 50% that at-least two people in the room have same birthday?
Answer: 23
The number is surprisingly very low. In fact, we need only 70 people to make the probability 99.9 %.
Let us discuss the generalized formula.
What is the probability that two persons among n have same birthday?
Let the probability that two people in a room with n have same birthday be P(same). P(Same) can be easily evaluated in terms of P(different) where P(different) is the probability that all of them have different birthday.
P(same) = 1 – P(different)
P(different) can be written as 1 x (364/365) x (363/365) x (362/365) x …. x (1 – (n-1)/365)
How did we get the above expression?
Persons from first to last can get birthdays in following order for all birthdays to be distinct:
The first person can have any birthday among 365
The second person should have a birthday which is not same as first person
The third person should have a birthday which is not same as first two persons.
…………….
……………
The n’th person should have a birthday which is not same as any of the earlier considered (n-1) persons.
Approximation of above expression
The above expression can be approximated using Taylor’s Series.
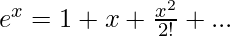
provides a first-order approximation for ex for x << 1:
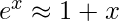
To apply this approximation to the first expression derived for p(different), set x = -a / 365. Thus,
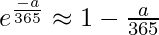
The above expression derived for p(different) can be written as
1 x (1 – 1/365) x (1 – 2/365) x (1 – 3/365) x …. x (1 – (n-1)/365)
By putting the value of 1 – a/365 as e-a/365, we get following.
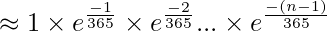
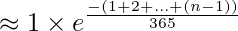
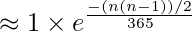
Therefore,
p(same) = 1- p(different)
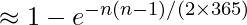
An even coarser approximation is given by
p(same)
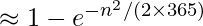
By taking Log on both sides, we get the reverse formula.
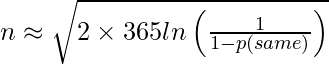
Using the above approximate formula, we can approximate number of people for a given probability. For example the following C++ function find() returns the smallest n for which the probability is greater than the given p.
Implementation of approximate formula.
The following is program to approximate number of people for a given probability.
C++
#include <cmath>
#include <iostream>
using namespace std;
int find(double p)
{
return ceil(sqrt(2*365*log(1/(1-p))));
}
int main()
{
cout << find(0.70);
}
|
Java
class GFG {
static double find(double p) {
return Math.ceil(Math.sqrt(2 *
365 * Math.log(1 / (1 - p))));
}
public static void main(String[] args)
{
System.out.println(find(0.70));
}
}
|
Python3
import math
def find( p ):
return math.ceil(math.sqrt(2 * 365 *
math.log(1/(1-p))));
print(find(0.70))
|
C#
using System;
class GFG {
static double find(double p) {
return Math.Ceiling(Math.Sqrt(2 *
365 * Math.Log(1 / (1 - p))));
}
public static void Main()
{
Console.Write(find(0.70));
}
}
|
PHP
<?php
function find( $p)
{
return ceil(sqrt(2 * 365 *
log(1 / (1 - $p))));
}
echo find(0.70);
?>
|
Javascript
<script>
function find( p){
return Math.ceil(Math.sqrt(2*365*Math.log(1/(1-p))));
}
document.write(find(0.70));
</script>
|
Time Complexity: O(log n)
Auxiliary Space: O(1)
Source:
http://en.wikipedia.org/wiki/Birthday_problem
Applications:
1) Birthday Paradox is generally discussed with hashing to show importance of collision handling even for a small set of keys.
2) Birthday Attack
Below is an implementation:
C
#include<stdio.h>
int main(){
float num = 365;
float denom = 365;
float pr;
int n = 0;
printf("Probability to find : ");
scanf("%f", &pr);
float p = 1;
while (p > pr){
p *= (num/denom);
num--;
n++;
}
printf("\nTotal no. of people out of which there "
" is %0.1f probability that two of them "
"have same birthdays is %d ", p, n);
return 0;
}
|
C++
#include <bits/stdc++.h>
using namespace std;
int main(){
float num = 365;
float denom = 365;
float pr;
int n = 0;
cout << "Probability to find : " << endl;
cin >> pr;
float p = 1;
while (p > pr){
p *= (num/denom);
num--;
n++;
}
cout << " Total no. of people out of which there is " << p
<< "probability that two of them have same birthdays is " << n << endl;
return 0;
}
|
Java
class GFG{
public static void main(String[] args){
float num = 365;
float denom = 365;
double pr=0.7;
int n = 0;
float p = 1;
while (p > pr){
p *= (num/denom);
num--;
n++;
}
System.out.printf("\nTotal no. of people out of which there is ");
System.out.printf( "%.1f probability that two of them "
+ "have same birthdays is %d ", p, n);
}
}
|
Python3
if __name__ == '__main__':
num = 365;
denom = 365;
pr = 0.7;
n = 0;
p = 1;
while (p > pr):
p *= (num / denom);
num -= 1;
n += 1;
print("Total no. of people out of which there is ", end="");
print ("{0:.1f}".format(p), end="")
print(" probability that two of them " + "have same birthdays is ", n);
|
C#
using System;
public class GFG {
public static void Main(String[] args) {
float num = 365;
float denom = 365;
double pr = 0.7;
int n = 0;
float p = 1;
while (p > pr) {
p *= (num / denom);
num--;
n++;
}
Console.Write("\nTotal no. of people out of which there is ");
Console.Write("{0:F1} probability that two of them have same birthdays is {1} ", p, n);
}
}
|
Javascript
<script>
var num = 365;
var denom = 365;
var pr = 0.7;
var n = 0;
var p = 1;
while (p > pr) {
p *= (num / denom);
num--;
n++;
}
document.write("\nTotal no. of people out of which there is ");
document.write(p.toFixed(1)+" probability that two of them " + "have same birthdays is "+ n);
</script>
|
OutputProbability to find :
Total no. of people out of which there is 0.0 probability that two of them have same birthdays is 239
Time Complexity: O(log n)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...