Section formula for 3 D
Last Updated :
28 Jan, 2024
Given two coordinates (x1, y1, z1) and (x2, y2, z2) in 3D, and m and n, find the co-ordinates that divides the line joining (x1, y1, Z1) and (x2, y2, Z2) in the ratio m : n.
Examples:
Input : x1 = 2, y1 = -1, Z1 = 4, x2 = 4, y2 = 3, Z2 = 2,
m = 2, n = 3
Output : (2.8, .6, 3.2)
Explanation: co-ordinates (2.8, .6, 3.2)
divides the line in ratio 2 : 3
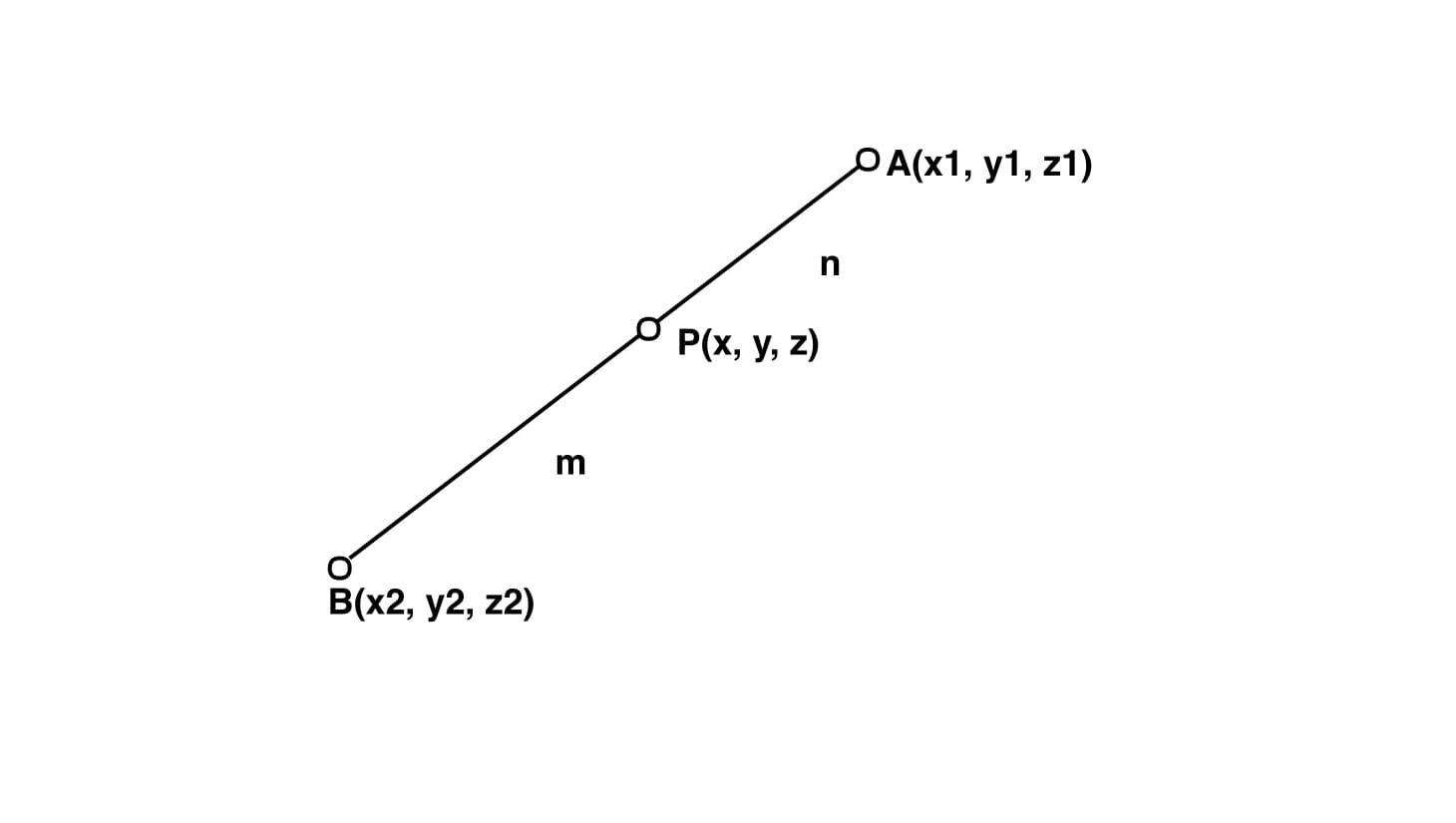
Approach:
Given two coordinates A(x1, y1, Z1) and B(x2, y2, Z2) in 3D, and m and n, we have to find the co-ordinates that divides the line joining (x1, y1, Z1) and (x2, y2, Z2) in the ratio m : n.
Let the co-ordinates will be P(x, y, z)
then according to section fORmula in 3 D
x = (m * x2 + n * x1) / (m + n)
y = (m * y2 + n * y1) / (m + n)
z = (m * z2 + n * z1) / (m + n)
Below is the implementation of above approach:
C++
#include <iostream>
using namespace std;
void section(double x1, double x2, double y1,
double y2, double z1, double z2,
double m, double n)
{
double x = ((m * x2) + (n * x1)) / (m + n);
double y = ((m * y2) + (n * y1)) / (m + n);
double z = ((m * z2) + (n * z1)) / (m + n);
cout << "(" << x << ", ";
cout << y << ", ";
cout << z << ")" << endl;
}
int main()
{
double x1 = 2, x2 = 4, y1 = -1,
y2 = 3, z1 = 4, z2 = 2,
m = 2, n = 3;
section(x1, x2, y1, y2, z1, z2, m, n);
return 0;
}
|
Java
import java.util.*;
class solution
{
static void section(double x1, double x2, double y1,
double y2, double z1, double z2,
double m, double n)
{
double x = ((m * x2) + (n * x1)) / (m + n);
double y = ((m * y2) + (n * y1)) / (m + n);
double z = ((m * z2) + (n * z1)) / (m + n);
System.out.print( "(" +x +", ");
System.out.print( y+ ", ");
System.out.println(z + ")" );
}
public static void main(String arr[])
{
double x1 = 2, x2 = 4, y1 = -1,
y2 = 3, z1 = 4, z2 = 2,
m = 2, n = 3;
section(x1, x2, y1, y2, z1, z2, m, n);
}
}
|
Python3
def section(x1, x2, y1, y2, z1, z2, m, n):
x = ((m * x2) + (n * x1)) / (m + n)
y = ((m * y2) + (n * y1)) / (m + n)
z = ((m * z2) + (n * z1)) / (m + n)
print("(",x,",",y,",",z,")")
if __name__ == '__main__':
x1 = 2
x2 = 4
y1 = -1
y2 = 3
z1 = 4
z2 = 2
m = 2
n = 3
section(x1, x2, y1, y2, z1, z2, m, n)
|
C#
using System;
class GFG
{
static void section(double x1, double x2, double y1,
double y2, double z1, double z2,
double m, double n)
{
double x = ((m * x2) + (n * x1)) / (m + n);
double y = ((m * y2) + (n * y1)) / (m + n);
double z = ((m * z2) + (n * z1)) / (m + n);
Console.Write("(" + x +", ");
Console.Write(y + ", ");
Console.WriteLine(z + ")" );
}
static public void Main ()
{
double x1 = 2, x2 = 4, y1 = -1,
y2 = 3, z1 = 4, z2 = 2,
m = 2, n = 3;
section(x1, x2, y1, y2, z1, z2, m, n);
}
}
|
Javascript
<script>
function section(x1, x2, y1, y2, z1, z2, m, n)
{
let x = ((m * x2) + (n * x1)) / (m + n);
let y = ((m * y2) + (n * y1)) / (m + n);
let z = ((m * z2) + (n * z1)) / (m + n);
document.write("(" + x +", ");
document.write(y + ", ");
document.write(z + ")" );
}
let x1 = 2, x2 = 4, y1 = -1,
y2 = 3, z1 = 4, z2 = 2,
m = 2, n = 3;
section(x1, x2, y1, y2, z1, z2, m, n);
</script>
|
PHP
<?php
function section($x1, $x2, $y1,
$y2, $z1, $z2,
$m, $n)
{
$x = (($m * $x2) + ($n * $x1)) / ($m + $n);
$y = (($m * $y2) + ($n * $y1)) / ($m + $n);
$z = (($m * $z2) + ($n * $z1)) / ($m + $n);
echo "(" . $x . ", ";
echo $y . ", ";
echo $z . ")" ."\n";
}
$x1 = 2; $x2 = 4; $y1 = -1;
$y2 = 3; $z1 = 4; $z2 = 2;
$m = 2; $n = 3;
section($x1, $x2, $y1, $y2,
$z1, $z2, $m, $n);
|
Time complexity: O(1) because it is performing constant operations
Auxiliary space: O(1)
Share your thoughts in the comments
Please Login to comment...