Section formula (Point that divides a line in given ratio)
Last Updated :
28 Jan, 2024
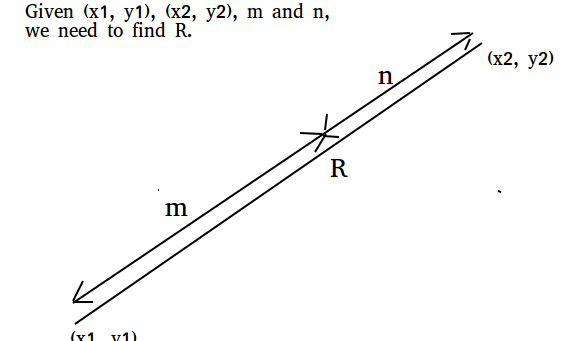
Given two coordinates (x1, y1) and (x2, y2), and m and n, find the co-ordinates that divides the line joining (x1, y1) and (x2, y2) in the ratio m : n
Examples:
Input : x1 = 1, y1 = 0, x2 = 2 y2 = 5,
m = 1, n = 1
Output : (1.5, 2.5)
Explanation: co-ordinates (1.5, 2.5)
divides the line in ratio 1 : 1
Input : x1 = 2, y1 = 4, x2 = 4, y2 = 6,
m = 2, n = 3
Output : (2.8, 4.8)
Explanation: (2.8, 4.8) divides the line
in the ratio 2:3
The section formula tells us the coordinates of the point which divides a given line segment into two parts such that their lengths are in the ratio m : n

C++
#include <iostream>
using namespace std;
void section(double x1, double x2, double y1,
double y2, double m, double n)
{
double x = ((n * x1) + (m * x2)) /
(m + n);
double y = ((n * y1) + (m * y2)) /
(m + n);
cout << "(" << x << ", ";
cout << y << ")" << endl;
}
int main()
{
double x1 = 2, x2 = 4, y1 = 4,
y2 = 6, m = 2, n = 3;
section(x1, x2, y1, y2, m, n);
return 0;
}
|
Java
import java.io.*;
class sections {
static void section(double x1, double x2,
double y1, double y2,
double m, double n)
{
double x = ((n * x1) + (m * x2)) /
(m + n);
double y = ((n * y1) + (m * y2)) /
(m + n);
System.out.println("(" + x + ", " + y + ")");
}
public static void main(String[] args)
{
double x1 = 2, x2 = 4, y1 = 4,
y2 = 6, m = 2, n = 3;
section(x1, x2, y1, y2, m, n);
}
}
|
Python
def section(x1, x2, y1, y2, m, n):
x = (float)((n * x1)+(m * x2))/(m + n)
y = (float)((n * y1)+(m * y2))/(m + n)
print (x, y)
x1 = 2
x2 = 4
y1 = 4
y2 = 6
m = 2
n = 3
section(x1, x2, y1, y2, m, n)
|
C#
using System;
class GFG {
static void section(double x1, double x2,
double y1, double y2,
double m, double n)
{
double x = ((n * x1) + (m * x2)) /
(m + n);
double y = ((n * y1) + (m * y2)) /
(m + n);
Console.WriteLine("(" + x + ", " + y + ")");
}
public static void Main()
{
double x1 = 2, x2 = 4, y1 = 4,
y2 = 6, m = 2, n = 3;
section(x1, x2, y1, y2, m, n);
}
}
|
Javascript
<script>
function section(x1, x2, y1, y2, m, n)
{
let x = ((n * x1) + (m * x2)) /
(m + n);
let y = ((n * y1) + (m * y2)) /
(m + n);
document.write("(" + x + ", " + y + ")");
}
let x1 = 2, x2 = 4, y1 = 4,
y2 = 6, m = 2, n = 3;
section(x1, x2, y1, y2, m, n)
</script>
|
PHP
<?php
function section($x1, $x2, $y1,
$y2, $m, $n)
{
$x = (($n * $x1) + ($m * $x2))
/ ($m + $n);
$y = (($n * $y1) + ($m * $y2))
/ ($m + $n);
echo("(" . $x . ", ");
echo($y . ")");
}
$x1 = 2; $x2 = 4; $y1 = 4;
$y2 = 6; $m = 2; $n = 3;
section($x1, $x2, $y1, $y2, $m, $n);
?>
|
Output:
(2.8, 4.8)
Time Complexity: O(1)
Auxiliary Space: O(1)
How does this work?

From our diagram, we can see,
PS = x – x1 and RT = x2 – x
We are given,
PR/QR = m/n
Using similarity, we can write
RS/QT = PS/RT = PR/QR
Therefore, we can write
PS/RR = m/n
(x - x1) / (x2 - x) = m/n
From above, we get
x = (mx2 + nx1) / (m + n)
Similarly, we can solve for y.
References:
http://doubleroot.in/lessons/coordinate-geometry-basics/section-formula/#.WjYXQvbhU8o
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...