Second Derivative Test

Last Updated : 28 Sep, 2023

Second Derivative Test is one of the methods in calculus to find the maxima and minima of a curve. Other than, the second derivative test there is also a first derivative, which can be referred to as a rudimentary version of the second derivative test.

First derivative test helps us find critical points for a given function but does not tell us about the nature of the function at these points. We also come across cases where we cannot get critical points as the first derivative test fails. Second derivative test is used in these cases. The second derivative test clearly tells us if the critical point obtained is a point of local maximum or local minimum. Second derivative test is also helpful in solving various problems in different fields such as science, physics, and engineering. In this article, we shall discuss the second derivative test in detail.

Second-Derivative-Test

Table of Content

What is Second Derivative Test?
Steps for Second Derivative Test for Maxima and Minima
Examples of Second Derivative Test
Uses of Second Derivative Test
Difference between First and Second Derivative Test
Multivariable Second Derivative Test

What is Second Derivative Test?

Second derivative test is used to find the points of local maximum and local minimum in those cases where the first derivative test fails. It involves differentiating the function twice and then calculating its value on the critical points. Thus it must be noted that the second derivative test holds true for functions that can be differentiated twice.

Steps for Second Derivative Test for Maxima and Minima

Consider a real-valued function f(x) which is defined on a closed or bounded interval [a, b]. Let k be a point in this interval.

In order to conduct the second derivative test on a function f(x), the following steps are followed:

Differentiate the function f(x) with respect to x to get f'(x).
Now further differentiate f'(x) with respect to x to get f”(x) i.e. the second derivative of f(x).
Equate the value of f'(x) to 0 to get the values of x at which f'(x) becomes zero.
Now calculate the value of f”(x) at points obtained.

On calculating the value of f”(k), we can arrive at the following three conditions:

Case 1: Local Minima

If f'(x) = 0 and k is the required point, then if f”(k) > 0, the point k is said to be the point of local minima.

Case 2: Local Maxima

If f'(x) = 0 and k is the required point, then if f”(k) < 0, the point k is said to be the point of local maxima.

Case 3: Point of Inflection

If f'(k) = 0 and k is the required point, then if f”(x) = 0, the point k is said to be the point of inflection and the function is said to have no point of local maxima and minima.

Learn more about Inflection Point.

Example of Second Derivative Test

Let us understand how to find local maxima and minima using second derivative test using the below example:

Example: Find local maxima or local minima of the function f(x) = x³ – 6x.

Solution:

Given f(x) = x³-6x

In order to calculate the local maxima and local minima, differentiate f(x) w.r.t x

f'(x) = 3x² – 6

Equate f'(x) to 0

3x² – 6 = 0

⇒ 3x² = 6

⇒ x = √2 or -√2

Now calculate f”(x)

f”(x) = 6x

At x = √2, f”(√2) = 6√2 > 0. This means that x = √2 is the point of local minima.

At x = -√2, f”(-√2) = -6√2 < 0. This means that x = -√2 is the point of local maxima.

Uses of Second Derivative Test

Second derivative test is useful in the following cases:

Second Derivative Test is used to calculate the points of local maxima and local minima where the first derivative fails.
It can also help us to determine the extremities of the curve.
It can also help us to know about the orientation of a parabola.
In various fields such as physics, economic and engineering, Second Derivative Test comes in very handy to find optimal solutions to various problems.
Second Derivative Test also helps us determine the concavity and convexity of the curve.

First and Second Derivative Test

The first derivative test and second derivative test both are used to find local maxima and minima but there is certain difference between the two. The following table lists the key differences between both the tests.

Test	First Derivative Test	Second Derivative Test
Critical Point	Where f'(x) = 0 or f'(x) is undefined	Where f'(x) = 0 or f'(x) is undefined
Local Minima	f'(x) changes from negative to positive	f”(x) > 0 at the critical point
Local Maxima	f'(x) changes from positive to negative	f”(x) < 0 at the critical point
Neither Minima nor Maxima	f'(x) fails to exit.	f”(x) = 0 (inconclusive)

Multivariable Second Derivative Test

Multivariable second derivative test is used in case when the given function has two variable (say x and y). This method makes use of partial differentiation to find the local maxima and local minima. According to this test:

Let f be a function with two variables x and y.
Take partial derivatives of function f with respect to each variable and set them equal to 0. Solve the equations obtained to get the values of x and y.
Let:

$D (x, y) = \frac{\partial ^ 2f}{\partial x^2} - \frac{\partial ^ 2f}{\partial y^2} - (\frac{\partial ^ 2f}{\partial x \partial y})^2$

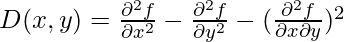
If D(x, y) < 0 then f has a saddle point at x and y
If D(x, y) = 0 then the test fails
If D(x, y) > 0 then,
- If 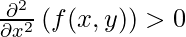$\frac{\partial ^ 2}{\partial x^2} \left(f(x, y)\right) > 0$ , then (x, y) is the point of local minima
- If 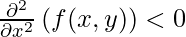$\frac{\partial ^ 2}{\partial x^2}\left(f(x, y)\right)< 0$ , then (x, y) is the point of local maxima

Solved Examples of Second Derivative Test

Example 1: Find the point of local maxima and local minima of the function x³ – 12x using second derivative test.

Solution:

Given f(x) = x³-12x

In order to calculate the local maxima and local minima, differentiate f(x) w.r.t x

f'(x) = 3x² – 12

Equate f'(x) to 0

3x²– 12 = 0

⇒ 3x² = 12

⇒ x = 2 or -2

Now calculate f”(x)

f”(x) = 6x

At x = 2, f”(2) = 12 > 0. This means that x = 2 is the point of local minima.

At x = -2, f”(-2) = -12 < 0. This means that x = -2 is the point of local maxima.

Example 2: Find the point of local maxima and local minima of the function x³ – x² – 5x using second derivative test.

Solution:

Given f(x) = x³-x²– 5x

In order to calculate the local maxima and local minima, differentiate f(x) w.r.t x

f'(x) = 3x² – 2x – 5

Equate f'(x) to 0

3x² – 2x – 5 = 0

⇒ $x = \frac{2\pm \sqrt{4-4(3)(-5)}}{2(3)} \\ \implies x = \frac{2\pm \sqrt{64}}{6} \\ \implies x = \frac{5}{3}~or~-1$

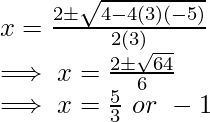
Now calculate f”(x)

f”(x) = 6x – 2

At x = 5/3, f”(5/3) = 8 > 0. This means that x = 5/3 is the point of local minima.

At x = -1, f”(-1) = -8 < 0. This means that x = -1 is the point of local maxima.

Example 3: Find the point of local maxima and local minima of the function x⁴– x²using second derivative test.

Solution:

Given f(x) = x⁴-x²

In order to calculate the local maxima and local minima, differentiate f(x) w.r.t x

f'(x) = 4x³ – 2x

Equate f'(x) to 0

4x³ – 2x = 0

⇒ 4x³ = 2x

⇒ 2x² = 1

x = 1/√2 or -1√2

Now calculate f”(x)

f”(x) = 12x² – 2

At x = 1/√2, f”(1/√2) = 4 > 0. This means that x = 1/√2 is the point of local minima.

At x = -1/√2, f”(-1/√2) = -8 < 0. This means that x = -1/√2 is the point of local maxima.

Example 4: A bus is moving along the curve 2y = 2x²+10. A man standing at point (3,5) wants to find the nearest distance between him and bus. Calculate the nearest distance.

Solution:

Given 2y = 2x² + 10

⇒ y = x²+ 10

f(x) = x² + 5

We need to calculate the nearest distance which means minimum distance. Let the distance be minimum when bus is at a point (x, y)

Distance of point (3, 5) from the point (x, y) = D = √(x-3)²+(y-5)²

D² = (x-3)² + (y-5)²

Substituting the value of y = x² + 5

D² = (x-3)² + (x²)²……………….(1)

D is minimum when D² is minimum. Thus we will calculate D’

D’ = 2(x-3) + 4x³

D’ = 2x – 6 + 4x³

D’ = (x−1)(4x²+4x+6) = 2(x−1)(2x²+2x+3)

Equating D’ = 0

x-1 = 0 or 2x²+2x+3 = 0

⇒x = 1 OR

$⇒ x = \frac{-2\pm \sqrt{4-4(2)(3)}}{2(2)} \\ \implies x = \frac{-2\pm \sqrt{-20}}{4}$

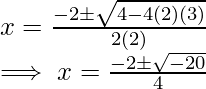
This is not possible as x does not assume real value

Thus x = 1

Now D” = 2+12x²

At x =1, D” = 14 > 0. Thus x = 1 is the point of local minima.

Thus minimum distance is at x = 1 which is calculated by substituting x = 1 in equation (1)

D² = 4 + 1 = 5

D = √5

Thus the minimum distance is √5

Example 5: Calculate the maximum height of a cricket ball if its height is given by the function h(x) = 2x³-12x²+1 using second derivative test.

Solution:

Given h(x) = 2x³– 12x²+1

We need to calculate the maximum height.

In order to calculate the maximum height, differentiate h(x) w.r.t x

h'(x) = 6x²– 24x

Equate h'(x) to 0

6x²– 24x = 0

⇒ 6x(x-4) = 0

⇒ x = 0 or 4

Now calculate f”(x)

h”(x) = 12x – 24

At x = 0, h”(0) = -24 < 0. This means that x = 1/√2 is the point of local maxima.

At x = 4, h”(4) = 24 > 0. This means that x = -1/√2 is the point of local minima.

Thus the height is maximum at a x = 0.

Maximum height = h(0) = 2(0)³-12(0) + 1 = 1 unit

Example 6: Find the point of local maxima and local minima of the function x⁴ – 12x³ using second derivative test.

Solution:

Given f(x) = x⁴ – 12x³

In order to calculate the local maxima and local minima, differentiate f(x) w.r.t x

f'(x) = 4x³ – 36x²

Equate f'(x) to 0

4x³ – 36x² = 0

⇒ 4x²(x-9) = 0

⇒ x = 0 or 9

Now calculate f”(x)

f”(x) = 12x² – 72x

At x = 0, f”(0) = 0 > 0. This means that x = 0 is the point of inflection.

At x = 9, f”(9) = 12(9)²-72(9) = 324 > 0. This means that x = 9 is the point of local minima.

Example 7: Find the point of local maxima or local minima of the function x² – 1 using second derivative test.

Solution:

Given f(x) = x² – 1

In order to calculate the local maxima and local minima, differentiate f(x) w.r.t x

f'(x) = 2x

Equate f'(x) to 0

2x = 0

⇒ x = 0

Now calculate f”(x)

f”(x) = 2

At x = 0, f”(0) = 2 > 0. This means that x = 0 is the point of local minima.

Example 8: Find the point of local maxima and local minima of the function 2x² – 3x using second derivative test.

Solution:

Given f(x) = 2x² – 3x

In order to calculate the local maxima and local minima, differentiate f(x) w.r.t x

f'(x) = 4x – 3

Equate f'(x) to 0

4x – 3 = 0

⇒ x = 3/4

Now calculate f”(x)

f”(x) = 4

At x = 3/4, f”(3/4) = 4 > 0. This means that x = 3/4 is the point of local minima.