Resolution Completeness and clauses in Artificial Intelligence
Last Updated :
06 Feb, 2024
Prerequisite:
To wrap up our resolution topic, we’ll try to understand why PL-RESOLUTION is complete. To accomplish so, we propose the resolution closure 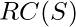 of a collection of clauses
of a collection of clauses 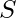 , which is the set of all clauses derivable from clauses in
, which is the set of all clauses derivable from clauses in 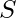 or their derivatives by applying the resolution rule repeatedly. The resolution closure is the final value of the variable clauses computed by PL-RESOLUTION. Because there are only a limited number of separate phrases that can be created from the symbols
or their derivatives by applying the resolution rule repeatedly. The resolution closure is the final value of the variable clauses computed by PL-RESOLUTION. Because there are only a limited number of separate phrases that can be created from the symbols  that exist in S,
that exist in S, 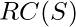 must be finite. (Note that without the factoring phase, which eliminates numerous copies of literal, this would not be true.) As a result, PL-RESOLUTION always ends.
must be finite. (Note that without the factoring phase, which eliminates numerous copies of literal, this would not be true.) As a result, PL-RESOLUTION always ends.
The ground resolution theorem is a completeness theorem for resolution in propositional logic: If a group of clauses is unsatisfiable, the empty clause is included in the resolution closure of those clauses.
The contrapositive of this theorem is demonstrated: if the closure 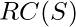 does not contain the empty clause, then
does not contain the empty clause, then 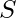 is satisfiable. In reality, we can build a model for
is satisfiable. In reality, we can build a model for 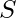 that includes appropriate truth values for
that includes appropriate truth values for  . The following is the building procedure: For
. The following is the building procedure: For 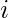 from 1 to k, assign false to
from 1 to k, assign false to 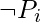 if a clause in
if a clause in 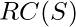 has the literal
has the literal 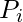 and all of its other literals are false under the assignment specified for
and all of its other literals are false under the assignment specified for 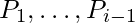 Otherwise,
Otherwise, 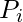 should be set to true.
should be set to true.
This assignment to  . Assume the opposite—that assigning symbol
. Assume the opposite—that assigning symbol 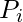 at some point
at some point 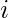 in the sequence causes some sentence
in the sequence causes some sentence 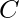 to become false. For this to happen, all other literals in
to become false. For this to happen, all other literals in 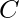 must have already been faked by assignments to
must have already been faked by assignments to 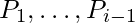 . As a result,
. As a result, 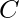 must now resemble either
must now resemble either 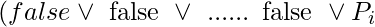 or
or 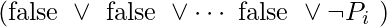 . If just one of these clauses is in
. If just one of these clauses is in 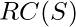 , the algorithm will give the necessary truth value to Pi to make
, the algorithm will give the necessary truth value to Pi to make 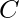 true, therefore
true, therefore 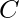 can only be falsified if both are in
can only be falsified if both are in 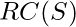 . Now, because
. Now, because 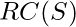 is closed during resolution, it will include the resolvent of these two clauses, which will have all of its literal falsified by the assignments to
is closed during resolution, it will include the resolvent of these two clauses, which will have all of its literal falsified by the assignments to 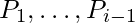 . This contradicts our belief that the first false clause arrives in stage
. This contradicts our belief that the first false clause arrives in stage 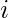 . As a result, we’ve established that the construction never falsifies a clause in
. As a result, we’ve established that the construction never falsifies a clause in 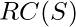 ; that is, it always creates a model of
; that is, it always creates a model of 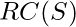 , and hence a model of S (because S is included in
, and hence a model of S (because S is included in 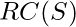 .
.
Definite and Horn Clauses
It is a highly essential inference method because of the completeness of resolution. However, in many cases, the entire strength of resolution isn’t required. Some real-world knowledge bases adhere to particular constraints on the types of sentences they include, allowing them to employ a more limited and efficient inference procedure.
The definite sentence, which is a disjunction of literals of which exactly one is affirmative, is one such constrained form. The sentence 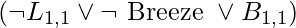 for example, is a definite clause, but
for example, is a definite clause, but 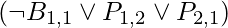 is not.
is not.
The Horn clause, which is a disjunction of literals, only one of which is affirmative, is a little more generic. All definite clauses, as well as clauses with no positive literals, are Horn clauses; they are referred to be goal clauses. Horn clauses are closed when they are resolved: when two Horn clauses are resolved, a Horn clause is returned.

This equation shows a grammar for Horn clauses, definite clauses, and conjunctive normal form. Although a clause is written as 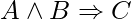 is still a definite clause when written as
is still a definite clause when written as 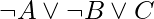 , only the former is regarded the standard form for definite clauses. Another type is the
, only the former is regarded the standard form for definite clauses. Another type is the 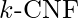 sentence, which is a CNF sentence with at most k literals in each clause.
sentence, which is a CNF sentence with at most k literals in each clause.
Only definite clause knowledge bases are interesting for three reasons:
- Every definite sentence can be inferred with a single positive literal as the conclusion and positive literal conjunction as the premise. The definite phrase
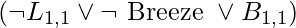 , for example, can be represented as the implication
, for example, can be represented as the implication 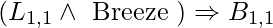 The phrase is simpler to grasp in its implication form: if the agent is in [1,1] and there is a wind, then [1,1] is breezy. The premise is known as the body, and the conclusion is known as the head in Horn form. A fact is a statement that consists of a single positive literal, such as
The phrase is simpler to grasp in its implication form: if the agent is in [1,1] and there is a wind, then [1,1] is breezy. The premise is known as the body, and the conclusion is known as the head in Horn form. A fact is a statement that consists of a single positive literal, such as 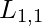 .
.  can also be stated in implication form, but it’s easier to just write
can also be stated in implication form, but it’s easier to just write 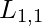 .
. - The forward-chaining and backward-chaining techniques may be used to infer using Horn clauses. Both of these algorithms are natural in the sense that the inference processes are clear and simple to follow for humans. Logic programming is based on this form of inference.
- Horn clauses may determine entailment in a time that is proportional to the size of the knowledge base, which is a nice surprise.
Share your thoughts in the comments
Please Login to comment...